-
Dla nauczyciela. Rachunki w tym rozdziale
Ćwiczenia w tym rozdziale wymagają wykonywania prostych obliczeń. Można je wykonać ręcznie lub w arkuszu kalkulacyjnym.
Komputery to narzędzia do przetwarzania informacji. Użytkownik komputera może tworzyć, modyfikować, czy po prostu przeglądać (oglądać, słuchać itd.) informacje, zapisane w dokumentach tekstowych, plikach graficznych czy wideo, skoroszytach arkusza kalkulacyjnego czy zbiorach baz danych. Gry komputerowe i inne programy-symulacje to przykłady tzw. wirtualnej rzeczywistości, która istnieje tylko w postaci informacji zapisanej pamięci komputera i wyświetlonej (po jej interpretacji) na ekranie monitora. Komputery pozwalają na wykonywanie obliczeń liczbowych, jak i na przesyłanie informacji przez sieć komputerową. To wszystko byłoby niemożliwe, gdyby nie wymyślono jakiegoś sposobu na zapis (reprezentację) różnego rodzaju informacji w pamięci operacyjnej komputera, na dysku twardym i ich przesyłania przez sieć komputerową.
Kluczową koncepcją, która pozwoliła uprościć trudności związane z projektowaniem i produkcją komputerów, ale również wpłynęła na niezawodność ich działania, jest koncepcja dwuwartościowego (dwustanowego) zapisu wszelkiego rodzaju informacji. Czasami mówi się o reprezentacji zero-jedynkowej (0-1), choć w praktyce (w realizacji fizycznej) możemy mieć do czynienia z czymkolwiek, co może przyjmować dwa stany. Na przykład dla pamięci elektronicznej będzie to oznaczać wysoką lub niską wartość napięcia prądu elektrycznego, a dla tradycyjnego dysku twardego -- namagnesowanie małych fragmentów warstw magnetycznych (północ -- południe).
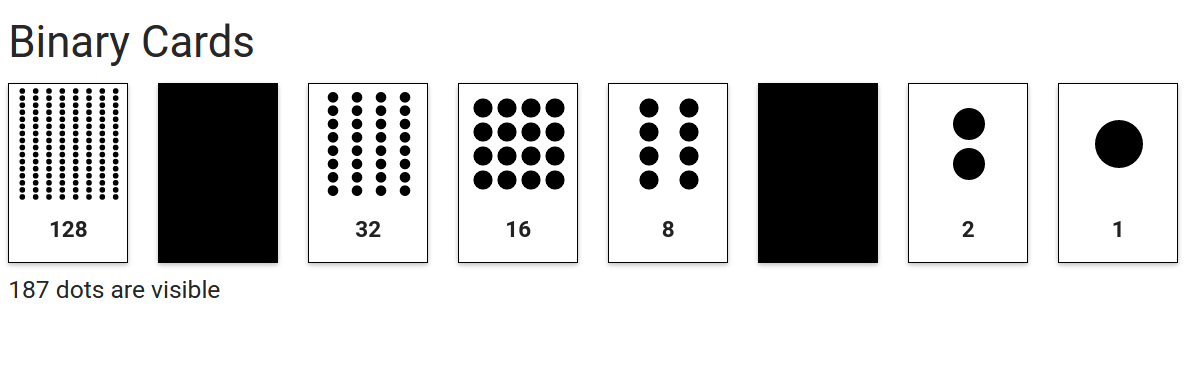
Pomysł, by wszystko w naszym cyfrowym świecie zapisywać z użyciem tylko dwóch wartości może wydawać się nieco fantastyczny. Oto ćwiczenie, które ukaże, jak zapisywać liczby, używając zestawu kart, które z jednej strony mają białe tło, a z drugiej strony -- czarne.
Zacznij od wskazania ostatniej karty (po prawej). Wtedy zobaczysz, że na stronie z białym tłem znajduje się pojedyncza czarna kropka.
Następnie wskaż na sąsiednią kartę, by na odwrocie zobaczyć dwie czarne kropki. Ile kropek kropek zobaczysz po odwróceniu kolejnej karty? Sprawdź! Staraj się odgadnąć liczbę kropek znajdujących się na kolejnych kartach.
Kolejne wyzwanie brzmi: Które karty należy odwrócić, aby łączna liczba kropek była równa 22? Jaka będzie odpowiedź dla liczby kropek równej: 11, 29 lub 19? Czy jakiejś liczby kropek nie sa się uzyskać? Możesz zacząć zliczanie od 0, jeśli chcesz.
-
Dla nauczyciela. Wskazówki dla nauczyciela
W czasie zajęć szkolnych zamiast aplikacji można użyć papierowych kart.
Jeśli uczniowie napotykają trudności w znalezieniu odpowiedzi na powyższe pytania, nauczyciel powinien wskazywać kolejne karty z lewej i stawiać pytania: „Czy karta z 16 kropkami jest porzebna? A karta z 8 kropkami?” itd. Uczniowie szybko przekonają się, że skuteczna jest metoda zachłanna: albo liczba kropek na karcie jest za duża, albo karty należy użyć.
Podczas pracy uczniowie powinni dostrzeć pewne prawidłowości.
Na przykład: Karta z jedną kropką jest odwracana, gdy pytanie dotyczy liczby nieparzystej.
-
Spojler. Rozwiązanie
Można zauważyć, że liczba kropek na kolejnej karcie jest dwa razy większa niż na sąsiedniej (po prawej). Dostrzeżenie tej prawidłowości jest istotne dla zrozumienia cyfrowego zapisu danych w komputerze.
Aby uzyskać liczbę kropek równą 22 potrzebujemy układu kart: „białe, czarne, białe, białe, czarne”. Liczbę 11 przedstawimy jako: „czarny, biały, czarny, biały, biały”. Liczbę 29 jako: „biały, biały, biały, czarny, biały”. Liczbę 19 jako: „biały, czarny, czarny, czarny, biały”.
Nietrudno odkryć, że dowolną liczbę z zakresu od 0 do 31 można przedstawić z użyciem 5 kart. Informację o liczbie, przedstawioną na karcie, można odczytać używając tylko dwóch słów: czarne lub białe. Na przykład informacja o liczbie 22 to ciąg słów: "biała, czarna, biała, biała, czarna" Każdy ciąg złożony ze ciągu słów czarne lub białe można zaś jednoznacznie przypisać pewnej liczbie. Np. "czarne, czarne, białe, białe, białe" odpowiada liczbie 7. Idea dwustanowego (binanrego) zapisu informacji stanowi podstawę zapisu danych w jakimkolwiek urządzeniu cyfrowym.
Gdy chcemy przedstawić na papierze to, co zapisano w komputerze, to zazwyczaj używamy „0” dla ilustracji jednego ze stanów i „1” – dla drugiego z nich. Oznacza to na przykład, że fragment pamięci elektronicznej komputera, dla którego wartości napięcia elektrycznego to:
niska,
niska,
wysoka,
niska,
wysoka,
wysoka,
wysoka,
wysoka,
niska,
wysoka,
niska,
niska
będziemy przedstawiać jako ciąg cyfr
0 0 1 0 1 1 1 1 0 1 0 0
Taka notacja jest powszechnie używana. Należy jednak pamiętać, że sformułowanie typu „komputer zapisuje informacje w postaci ciągu zer i jedynek” jest skrótem myślowym. Nie ma sposobu, żeby zrobić to bezpośrednio – komputery posługują się własnościami fizycznymi takimi jak wysokie i niskie napięcie, namagnesowanie północ/południe, czy ciemne i jasne materiały.
-
Co to jest?. Bity
Ponieważ używa się tylko dwóch cyfr: 0 i 1, więc mówi się o systemie dwójkowym lub binarnym (ang. binary system) i cyfrach dwójkowych (binarnych), zwanych bitami (ang. bit to skrót od słów „binary digit”). Pojęcie bitu jest jednym z najbardziej podstawowych w języku informatyków.
Każdy utworzony przez ciebie plik, każde zdjęcie zapisane na dysku komputera, każdy dokument pobrany z Internetu to po prostu krótszy lub dłuższy ciąg bitów, czyli cyfr dwójkowych. Dlatego mówi się o technologiach cyfrowych.
Choć informatycy na co dzień nie zajmują się bezpośrednio analizowaniem tych ciągów bitów, to wiedza na temat zasad binarnego zapisu informacji jest naprawdę istotna, gdyż pozwala np. na oszacowanie przestrzeni na dysku, potrzebnej do zapisu danych z odpowiednią jakością. Podczas lektury tekstów z różnych dziedzin informatyki możesz napotkać określenia typu „24-bitowy kolor”, „128-bitowe szyfrowanie”, „32-bitowy adres IP” czy „8-bitowy kod ASCII”. Wiedza na temat zapisu binarnego jest niezbędna informatykowi do oszacowania ilości miejsca na dysku potrzebnego do zapisania wysokiej jakości informacji o kolorze, określenia bezpieczeństwa wybranej metody szyfrowania, do wyboru odpowiedniej długości klucza podczas projektowania bazy danych, czy zastosowania kodowania odpowiedniego dla teksów języka, w których występują znaki spoza alfabetu języka angielskiego.
Ten rozdział przedstawia różne metody, jakie są używane w systemach komputerowych do zapisania różnego rodzaju informacji za pomocą ciągów bitów oraz to, jak wybór metody wpływa na koszt i jakość tego, co robimy na komputerze i czy w ogóle da się to zrobić.
Na początek przyjrzymy się kodowi (alfabetowi) Braille'a, który umożliwia zapisywanie i odczytywanie tekstów osobom niewidomym i niedowidzącym. Mimo że system brajlowski nie ma nic wspólnego z komputerami, to stanowi znakomite wprowadzenie do tematu tego rozdziału przewodnika po informatyce.
-
Informacja dodatkowa. Zapis znaków Braille'a
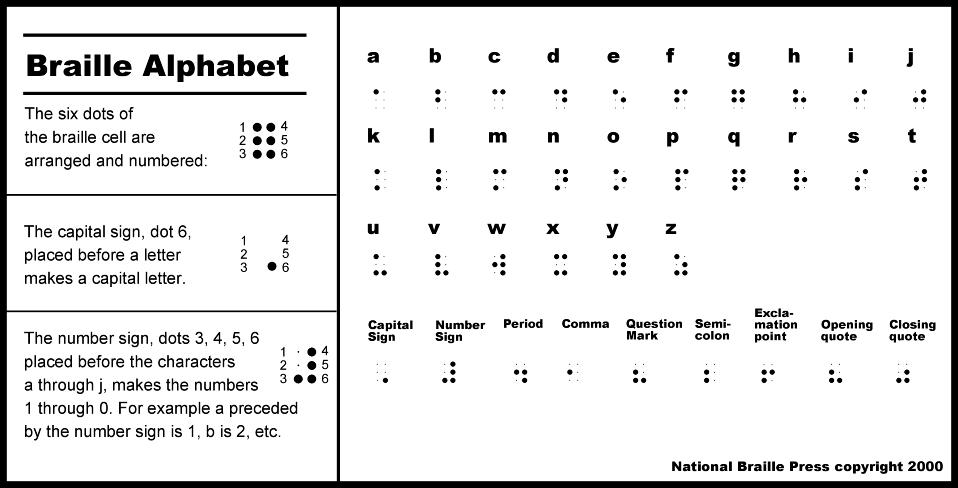
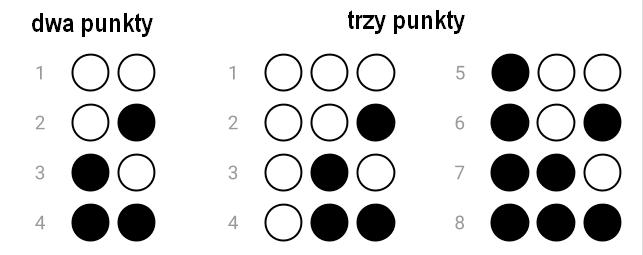
Dla uproszczenia ideę tzw. sześciopunktu można zilustrować używając sześciu małych kół ułożonych w dwóch kolumnach po trzy punkty w każdej. Koła z zamalowanym wnętrzem będą ilustracją punktów wypukłych.
Ponad 200 lat temu 15-letni Francuz wymyślił system zapisu tekstu (liter, cyfr, znaków przestankowych itd.) z użyciem tzw. sześciopunktów jako kombinacje sześciu wypukłych punktów ułożonych w dwóch kolumnach po trzy punkty w każdej. System stał się bardzo popularny wśród osób niewidomych, gdyż umożliwił względnie szybki i niezawodny sposób „czytania” tekstu. Alfabet Louisa Braille'a można uznać za jeden z pierwszych przykładów „binarnego” zapisu informacji – używa się w nim bowiem tylko dwóch znaków (wypukły punkt lub jego brak), a mimo to odpowiednie ich kombinacje pozwalają na wydawanie całych książek, zarówno fachowych, jak i literatury pięknej.
Sprawdźmy, ile różnych wzorców (znaków) w alfabecie Braille's można uzyskać, używając sześciopunktu. Gdyby system Braille'a używał kombinacji tylko dwóch (pary) punktów, to wzorców byłyby cztery. Gdyby używał kombinacji trzech punktów, to byłoby ich osiem.
Można było zauważyć, że w przypadku użycia trzech punktów liczba wzorców jest dwa razy większa niż dla przypadku dwóch punktów. Okazuje się, że dodanie każdego kolejnego punktu skutkuje podwojeniem liczby wzorców . To znaczy, że dla czterech punktów liczba wzorców będzie równa 16, dla pięciu – 32, a dla sześciu – 64. Dlaczego? Potrafisz to wyjaśnić?
-
Spojler. Wyjaśnienie
Po dodaniu czwartego punktu liczba wzorców podawaja się, bo nowy punkt można dołączyć do każdego wzorca 3-punktowego na dwa sposoby: jako punkt wypukły lub niewypukły. Podobnie można objaśnić przyczynę podwojenia się liczby wzorców po dodaniu czwartego punktu. To rozumowanie można uogólnić dla dowolnej liczby punktów.
-
Dla nauczyciela. O znaczeniu zrozumienia idei podawajania
Ta koncepcja (podwajanie się liczby wzorców) ma zasadnicze znaczenie dla zrozumienia istoty zapisu binarnego: każdy dodatkowy bit pozwala dwukrotnie zwiększyć liczbę wartości, które da się zapisać. Wybór odpowiedniej liczby bitów dla zapisu danych w konkretnej sytuacji jest bardzo ważny. Na przykład: 101-bitowy klucz szyfrowania jest dwa razy trudniej złamać, choć liczba użytych bitów jest większa tylko o 1%!
W obrębie sześciopunktu można uzyskać 64 wzorce. To wystarcza na oznaczenie liter alfabetu i innych znaków, takich jak np. cyfry czy znaki interpunkcyjne.
Kod Braille'a jest ilustracją zapisu z użyciem bitów. Istotnie, rozróżnia się dwa stany punktu (wypukły lub niewypukły), a każdy z wzorców tzw. sześciopunktu odpowiada innemu znakowi alfabetu. Na przykład litera m może być zapisana jako 110010, gdzie „1” oznacza punkt wypukły, a „0” niewypukły (przy założeniu, że czytamy od lewej do prawej i z góry na dół). W informatyce takich ciągów zer i jedynek używa się w analogiczny sposób do ukazania sposobu zapisu informacji w komputerze.
Alfabet Braille'a jest dobrą ilustracją przyczyn użyteczności zapisu binarnego. Można sobie wyobrazić system używający trzech rodzajów kropek: niewypukłych, półwypukłych i wypukłych. Z pewnością wprawny czytelnik potrafiłby je rozróżnić, a wtedy do uzyskania 64 znaków wystarczyłaby kombinacja czterech kropek. Kłopot w tym, że potrzebne byłyby bardziej dokładne urządzenia do tworzenia kropek, a ludzie musieliby więcej uwagi poświęcać rozróżnianiu kropek podczas „czytania”. Wystarczyłoby wtedy, że kartka zostałaby przygnieciona, nawet bardzo nieznacznie, a informacja stałby się nieczytelna.
Współczesne urządzenia cyfrowe prawie zawsze używają systemu dwustanowego (binarnego) do zapisu informacji. Przyczyny są podobne: dyski komputerowe i pamięć elektroniczna jest po prostu tańsza i mniejszych rozmiarów, jeśli wystarczy rozróżnić między dwoma skrajnymi wartościami (jak np. wysokie i niskie napięcie), a nie trzeba mierzyć subtelnych różnic w wartościach (np. między wartościami napięcia). Stosowanie systemu dziesiętnego byłoby niezwykle kosztowne.
-
Ciekawostka. Komputery oparte o system dziesiątkowy
Dlaczego w technice komputerowej używa się systemu dwójkowego? Czy nie można by używać systemu dziesiętnego? W przeszłości próbowano budować komputery oparte o system dziesiątkowy. Rozwiązania takie były wyjątkowo skomplikowane i kosztowne. Wymaganie, by rozróżniać 10 różnych stanów (wartości) oznacza większy stopień skomplikowania sprzętu do zapisu i odczytu (np. napięcia elektrycznego). O wiele łatwiej w praktyce realizować wymaganie, by rozróżniać dwa stany.
Dokładniejsze objaśnienie zalet praktycznych systemu binarnego znajduje się tutaj (po angielsku):
-
Dla nauczyciela. Rozgrzewka bez komputera
W ramach rozgrzewki można użyć ćwiczenia opisanego w scenariuszu 1 Zliczanie kropek zbioru scenariuszy lekcji bez komputera. Pojęcie systemu dwójkowego (binarnego) jest tam wprowadzone krok po kroku z użyciem wyłączniem prostych operacji zliczania i dodawania.
Oto aplikacja, w której odwzorowano tradycyjne karty czarno-białe:
Ten rozdział rozpocznie się od przypomnienia, czym jest system liczbowy. Ktoś mógłby sądzić, że takie matematyczne podejście „odstraszy” młodego czytelnika. Tymczasem większość uczniów powinna być dobrze obeznana z używaną w tekście terminologią, gdyż była wprowadzona w początkowych klasach szkoły podstawowej. Na lekcjach matematyki młodzież uczy się o notacji wykładniczej, więc zapis \(541 = 5 \times 10^2 + 4 \times 10^1 + 1 \times 10^0\) jest im dobrze znany. Tekst poniżej jest przypomnieniem, a nie objaśnianiem pojęcia systemu liczbowego po raz pierwszy. System dwójkowy (binarny) jest system liczbowym o podstawie 2. Zestawienie go z dobrze znanym młodziezy systemem o podstawie 10 powinno ułatawić zrozumienie istoty zagadnienia.
W tym rozdziale przyjrzymy się temu, jak w komputerach zapisuje się liczby. Zaczniemy od powtórzenia, czy jest system liczbowy o podstawie 10, którym posługujemy się na co dzień. Później spojrzymy na system binanry jak na sytem liczbowy o podstawie 2. W końcu będziemy chcieli wyjaśnić, jak zapisuje się w komputerze liczby ujemne i liczby niecałkowite.
Człowiek posługuje się zwykle pozycyjnym systemem liczbowym o podstawie 10 (zwanym też dziesiątkowym). Warto przypomnieć sobie koncepcję zapisu pozycyjnego, gdyż system dwójkowy (binarny) jest również systemem pozycyjnym, choć używa się w nim mniej cyfr!
Przykład: W kwocie 123 zł cyfra 3 odpowiada liczbie 3 zł, ale już cyfra 1 odpowiada kwocie 100 zł. Wartość (mnożnik) każdej z cyfr zależy od jej pozycji w zapisie. Mnożnik cyfry na danej pozycji jest 10 razy większy niż mnożnik cyfry na pozycji po prawej. W konsekwencji możemy mówić o jednościach, dziesiątkach, setkach, tysiącach, dziesiątkach tysięcy, setkach tysięcy, milionach itd. Na każdej z pozycji może wystąpić jedna z dziesięciu cyfr (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Np. liczba 90 328 może być zapisana w postaci sumy:
\(90328 = 90000 + 300 + 20 + 8\)
Liczbę tę można zapisać w postaci rozwinięcia (szeregu potęgowego):
\(90328 = (9 \times 10000) + (0 \times 1000) + (3 \times 100) + (2 \times 10) + (8 \times 1)\)
Bardziej formalnie można napisać tak:
\(90328 = (9 \times 10^4) + (0 \times 10^3) + (3 \times 10^2) + (2 \times 10^1) + (8 \times 10^0)\)
Oto kluczowe własności systemu dziesiątkowego:
- System używa 10 cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- Liczby to ciągi cyfr.
- O cyfrach tworzących zapis liczby mówimy, że znajdują się na odpowiednich pozycjach odpowiednio: jedności, dziesiątek, setek, tysięcy itd. Na przykład w liczbie 90 328 cyfra 3 jest na pozycji setek, a cyfra 2 na pozycji dziesiątek.
- Cyfra pierwsza po prawej (na pozycji jedności) ma najmniejszą wartość. Dlatego często nazywa się ją cyfrą najmniej znaczącą.
- Cyfra pierwsza po lewej ma największą wartość. Dlatego często nazywa się ją cyfrą najmniej znaczącą.
- Gdy stosujemy 10 cyfr, wtedy wartość cyfry na danej pozycji w liczbie jest 10 razy większa od wartości cyfry na pozycji po jej prawej stronie.
To, co zapisano powyżej, może brzmieć jako coś oczywistego. Warto to jednak przeanalizować dokładniej, gdyż pełną analogię dostrzeżemy we własnościach zapisu binarnego.
-
Dla nauczyciela. Jak uczyć o liczbach binarnych?
Ten podrozdział jest niezbędny do zrozumienia podrozdziału o cyfrowym zapisie informacji o kolorach.
Dla uczącego się kluczowe jest spostrzeżenie, że dodanie do binarnego zapisu liczby kolejnej cyfry oznacza podwojenie zakresu liczb, które da się zapisać z użyciem tylu cyfr. Poznanie pewnych prawidłowości właściwych zapisowi binarnemu i sprawne korzystanie z tej wiedzy przydaje się w wielu dziedzinach informatyki.
Binarne pianino to prosty środek dydaktyczny do nauki pewnej metody konwersji między systemami liczbowymi. Po wydrukowaniu uczniowie mogą wykonać samodzielne eksperymenty, które pozwolą zrozumieć istotę konwersji. Można je pobrać stąd. Wersja szablonu z czterema kopiami pianina jest tutaj. W obu wersjach stosuje się zapis 9-bitowy. W sytuacji, gdy wprowadzamy pojęcie bajta, uczniowie mogą 9. bit zignortować (ustawić na 0). Obecność 9. bitu na wydruku ma następujące uzasadnienie dydaktyczne: łatwo znaleźć największą liczbę 8-bitową: od wartości dziesiętnej 9. bitu wystarczy odjąć 1.
Jak wspomniano wcześniej, komputery zapisują informacje używając bitów, czyli rozróżniając tylko dwa możliwe stany. To oznacza, że w komputerze nie jest możliwe zapisanie liczby w systemie dziesiątkowym, używając cyfr od 0 do 9, jak to czyni człowiek. Używany jest system o podstawie 2, zwany dwójkowym (binarnym).
W systemie binarnym, można stosować wyłącznie dwie cyfry (0 i 1). W zapisie pozycyjnym mnożnik (wartość) każdej z cyfr jest więc dwa razy większy niż mnożnik cyfry po prawej stronie (inaczej niż w systemie dziesiątkowym, gdzie tym czynnikiem jest 10).
-
Ciekawostka. System dziesiątkowy -- denary system
System liczbowy o podstawie 10 (dziesiątkowy) w języku angielskim określa się słowami decimal lub denary. To drugie określenie, używane najczęściej w Wielkiej Brytanii, ma formę gramatyczną analogiczną do angielskiego binary (dwójkowy, binarny). Słowo „denary" ma ścisły związek z nazwą rzymskiej monety (denarius, po polsku: denar), która miała wartość 10 asów (wybijanych z miedzi lub brązu).
Aplikacja poniżej ma pomóc w zrozumieniu zasady zapisu binarnego. Warto wykonać kilka prób. Zapis dziesiątkowy liczby jest wyświetlany na końcu po prawej stronie.
Aby upewnić się, że właściwe posługujesz się narzędziem, sprawdź, czy po wpisaniu 101101 widzisz odpowiedź 45, po wpisaniu 100000 widzisz 32, a po wpisaniu 001010 jako reprezentacja dziesiętna pojawia się 10 dziesięć.
-
Dla nauczyciela. Używanie kalkulatora binarnego
W czasie używania powyższego kalkulatora binarnego uczniowie powinni odkryć, że zapis binarny liczby zapisanej w systemie dziesiątkowym mogą uzyskać cyfra po cyfrze (od lewej do prawej) postępując zachłannie w następujący sposób: cyfrę binarną ustawia się na 0 tylko i wyłącznie wówczas, gdy wstawienie jedynki sprawiłoby, że suma pokazana przez kalkulator jest większa od liczby poddawanej. Po wykonaniu kilku prób stanie się dla uczniów oczywiste, co należy robić. Z pewnością nawet młodsi uczniowie mogą istotę algorytmu odkryć samodzielnie. W konsekwencji pozwoli im to zdobyć pewność siebie i sprawność w zadaniach z konwersji na zapis binarny. Jeśli pomoc nauczyciela okaże się konieczna, to warto posłużyć się konkretnym przykładem. Na przykład dla liczby 37 nauczyciel zaczyna od ustawienia wszystkich bitów na 0 za wyjątkiem liczby na pozycji odpowiadającej liczbie 32 (która jest pierwszą nie przekraczającą 37). Następnie zachęca ucznia do odganięcia wartości bitu na pozycji odpowiadającej liczbie 16: ustawienie bitu na 1 oznaczałoby, że liczba jest nie mniejsza niż 48, więc bit trzeba ustawić na 0. Podobnie jest dla bitu na pozycji o wartości 8. Kolejny bit (odpowiadający składnikowi 4) należy ustawić na 1 (dostajemy sumę 36), następny na 0, a ostatni na 1 (suma: 37). Uzyskujemy zapis binarny: 100101. Wprawdzie metoda ta jest przedstawiona w wersji przewodnika dla uczniów, lecz lepiej byłoby, gdyby uczniowie odkryli ją samodzielnie.
W internecie można znaleźć wiele gier, które pomagają zgłębić temat liczb binarnych.
Istnieje inny algorytm konwersji, zwany metodą ilorazową, który często pojawia się w podręcznikach, zwłaszcza w podręcznikach programowania. Ma tę własność, że dość łatwo można go zapisać w języku programowania, ale trudniej zrozumieć jego poprawność. Prezentacja tego algorytmu nie jest niezbędna do zrozumienia dalszej części rozdziału. Cyfry binarne uzyskane w czasie działania algorytmu zapisuje się od prawej do lewej. Działa w następujący sposób: najmniej znaczący (skrajny prawy bit) ustawia się na 1, jeśli liczba zapisane dziesiętnie jest nieparzysta; w przeciwnym przypadku wartośc bitu jest równa 0. Następnie dzieli się liczbę przez 2 (w razie potrzeby zaokrąglając w dół do części całkowitej). Opisaną wyżej procedurę powtarza się dla kolejnych liczb uzyskanych w wyniku połowienia, aż do momentu uzyskania 0 jako wyniku dzielenia przez 2.
Znajdź zapis biarny liczb 4, 7, 12 i 57, używając kalkulatora binarnego.
Jaka jest największa liczba, jaką można uzyskać, posługując się tym narzędziem? Jaka jest najmniejsza? Czy jest jakaś liczba pomiędzy nimi, której nie jesteś w stanie uzyskać? Czy są liczby, które można zapisać w systemie binarnym na dwa różne sposoby? Odpowiedzi uzasadnij.
-
Spojler. Największe i najmniejsze liczby -- odpowiedzi
- 000000, czyli 0 (dziesiętnie) to najmniejsza liczba.
- 111111, czyli 63 (dziesiętnie) to największa liczba.
- Wszystkie liczby całkowite z zakresu od 0 do 63 da się zapisać binarnie (każdą wyłącznie w jeden sposób). Dokładnie tak samo, jak w systemie dziesiątkowym.
-
Dla nauczyciela. Zrozumienie jednoznaczności zapisu binarnego
Pytanie o jednoznaczność może być ciekawym wyzwaniem dla niektórych uczniów. Chodzi o to, że każdą liczbę można zapisać binarnym wyłącznie w jeden sposób; gdyby uczniowie mieli trudność w zrozumieniu uzasadnienia, to powinni przyjąć jednoznaczność zapisu na wiarę. Jednak można im pomóc zrozumieć ideę, proponując takie ćwiczenie: Uczeń otrzymuje zadanie zapisania pewnej liczby, np. 12, w systemie binarnym z użyciem 5 bitów. Skrajny lewy bit odpowiada wartości 16 (który jest większy od 12), więc należy ustawić go na 0 (ustawienie bitu na 1 na pewno nie pozwoli rozwiązać zadania). Dalej mamy bit o wartości 8. Nie jest możliwe zapisanie liczby 12 bez ustawienia tego bitu na 1 (suma wartości pozostałych bitów to 7). To oznacza, że 12 musi być zapisane jako 01100.
Innym sposobem na wykazanie jednoznaczaności zapisu binarnego jest wyznaczenie liczby wszystkich ciągów zero-jednykowych ustalonej długości. Dla przypadku 5 bitów mamy \(2^5\) (tj. 32) różnych ciągów odpowiadających 32 liczbom z zakresu od 0 do 31, co oznacza, że przyporządkowanie musi być jeden-do-jednego.
Prawdopodobnie jest już dla Ciebie jasne, że gdy lewy skrajny („najbardziej znaczący”) bit ustawiasz na 1, to liczbę powiększasz o 32. Podobnie ustawiając bity położone dalej na prawo, dodajesz odpowiednio 16, 8, 4, 2 i 1. Gdy bit ustawiasz na 0, liczba nie zwiększa się. Szukanie zapisu binarnego liczby jest więc związane z przedstawieniem liczby jako sumy niektórych lub wszystkich liczb ze zbioru: 32, 16, 8, 4, 2, 1, przy czym każda z liczb może wystąpić tylko raz.
Wybierz liczbę mniejszą niż 61 (np. numer twojego domu przy ulicy, wiek kolegi czy koleżanki, dzień miesiąca twojego urodzenia). Ustaw wszystkie cyfry binarne na 0, a następnie zacznij wybierać właściwe cyfry zaczynając od skrajnej lewej cyfry (32). Za każdym razem zdecyduj, czy wybrać 0 czy 1. Czy stosujesz metodę prób i błędów? Na czym polega twoja metoda zamiany (konwersji) liczb?
Czy potrafisz znaleźć zapis binarny liczby 23 bez posługiwania się narzędziem? A liczby 4, 0 i 32? Sprawdź teraz, czy dobrze myślisz, używając aplikacji.
-
Wyzwanie. Zliczanie binarne
Pomyśl, jak w sposób systematyczny liczyć w systemie binarnym, począwszy od 0, tj. 0, 1, 2, 3 itd. aż do największej liczby możliwej do zapisania z użyciem sześciu bitów. Zacznij od odliczenia od 0 do 16 i spróbuj dostrzec jakąś zasadę. Wskazówka: Wyobraź sobie, że dodajesz 1 do liczby zapisanej dziesiętnie, np. 7 + 1, 38 + 1, 19 +1, 99 + 1, 230 899 999 + 1 itd. Czy możesz ten sam pomysł zastosować dla liczb dwójkowych?
Pomyśl, jak zastosować wiedzę o systemie binarnym do liczenia na palcach powyżej liczby 10. Jaką największą liczbę można „zapisać” używając dziesięciu palców? Wyobraź sobie, że będziesz używać też palców u nóg. Jaka wówczas będzie odpowiedź?
-
Spojler. Rozwiązanie
Aby liczbę zapisaną binarnie powiększyć o 1, należy w jej zapisie binarnym począwszy od prawej zaieniać wartości bitów na przeciwne aż do pierwszego napotkanego 0 (włącznie). (W połowie przypadków tym poszukiwanym bitem 0 będzie skrajny prawy bit.)
Używając pięciu palców można policzyć do 31. W przypadku 10 palców największa liczba to 1023. Na YouTube można zobaczyć wiele przykładów wideo, na których ktoś liczby binarnie na palcach. Podczas prezentacji niektórzy posługują się rękawiczkami, na których odpowiednie palce są opisane liczbami: 16, 8, 4, 2, 1.
Co stałoby się, gdybyśmy mieli mniej niż sześć bitów? Przykład: Dla pięciu bitów, wartości na kolejnych pozycjach byłyby równe odpowiednio: 16, 8, 4, 2 i 1, więc największą liczbą byłaby 11111, czyli 31 (dziesiętnie). Liczba 14 zapisana na pięciu bitach to 01110.
-
Wyzwanie. Binarny zapis liczb
Zapisz podane liczby z użyciem odpowiedniej liczby bitów (o ile to możliwe).
- 101 na 7 bitach
- 28 na 10 bitach
- 7 na 3 bitach
- 18 na 4 bitach
- 28 232 na 16 bitach
-
Spojler. Odpowiedzi
Odpowiedzi (dla zwiększenia czytelności dodano odstępy co cztery bity, licząc od prawej):
- 101: 110 0101
- 28: 00 0001 1100
- 7: 111
- 18: niemożliwe na 4 bitach
- 28 232: 0110 1110 0100 1000
Ważnym pojęciem związanym z liczbami binarnymi jest zakres wartości, które można zapisać przy użyciu danej liczby bitów (cyfr). Pojedynczy bit wydaje się mało użyteczny, ale wystarczy do zapisania informacji np. o tym, co ktoś zaznaczył w formularzu internetowym dla pola wyboru tak/nie. Grupa ośmiu bitów jest już bardziej użyteczna – pozwala na zapis wartości od 0 do 255, a więc wystarczy do przechowania informacji o czyimś wieku, dniu miesiąca itd.
-
Co to jest?. Co to jest bajt?
Grupa ośmiu bitów jest tak użyteczna, że ma swoją nazwę: bajt (ang. byte). Pamięć elektroniczna i przestrzeń dyskowa jest zwykle podzielona na bajty. Większe liczby są zapisywane z użyciem większej liczby bajtów. Przykład: Dwa bajty (16 bitów) pozwalają na przechowywanie liczb z zakresu od 0 do 65 535. Cztery bajty (32 bity) umożliwiają zapis liczb aż do 4 294 967 295. Możesz sprawdzić, czy te liczby są poprawne, badając mnożniki odpowiadające bitom. Każdy kolejny bit oznacza podwojenie zakresu liczb.
Architektura dzisiejszych komputerów wymusza zapis liczb z użyciem 16, 32 lub 64 bitów. To wielokrotności bajtów (bajt to osiem bitów).
-
Ciekawostka. Binarny tort, czyli jak uchronić się od pożaru
Świeczki na torcie urodzinowym to przykład zastosowania systemu jedynkowego (unarnego). Kolejne liczby tworzy się przez powtarzanie znaku 1 tyle razy, ile wynika to z wartości danej liczby (można więc powiedzieć, że mnożnik dla każdej pozycji jest równy 1). Przykład: 3 to 111, a 10 to 1111111111. Wraz z wiekiem pojawi się problem – stulatek powinien uważać, aby nie wywołać pożaru, gdy będzie zdmuchiwać zapalone świeczki.
Na szczęście na torcie urodzinowym zamiast systemu jedynkowego można użyć dwójkowego: świeczka świeci się lub nie. Przykład: Na przyjęcie z okazji osiemnastych urodzin wystarczy pięć świeczek (i tylko dwie będą się świecić!), gdyż zapis binarny tej liczby to 10010.
Tutaj możesz zobaczyć wideo, na którym ktoś liczy na palcach do 1023, a ktoś innym otrzymuje „binarny” tort urodzinowy.
Komputery zapisują liczby binarne i posługują się nimi, przetwarzając dane. Na ekranie zwykle wyświetlane są już w postaci dziesiętnej, gdyż wielocyfrowy zapis dwójkowy byłby dla człowieka kompletnie nieczytelny. Czasami jednak musimy posłużyć się liczbami, które nie są zapisane dziesiętnie, np. przekazując innej osobie adres fizyczny karty sieciowej (adres MAC) lub określając precyzyjnie kolor na stronie internetowej (w kodzie HTML).
Wyobraź sobie, że masz przepisać na kartce 16-bitową liczbę: 0101001110010001. Można zastosować wówczas zapis skrócony: grupujemy cyfry po cztery (w tym przypadku: 0101 0011 1001 0001), i zastępujemy każdą czwórkę zapisem dziesiątkowym, co daje 5391. Pojawia się jednak mały problem: co z grupą bitów postaci 1111 (czyli 15)? Przecież mamy tylko cyfry od 0 do 9.
Rozwiązanie jest proste: wprowadzimy specjalne symbole dla czwórek bitów od 1010 (10) do 1111 (15), tj. posłużymy się literami od A do F. Na przykład liczbę 1011 1000 1110 0001 można w zwięzły sposób zapis tak: B8 E1. Litera "B" jest kodem dla 1011 (= 11 w systemie dziesiątkowym), a litera E jest kodem dla 1110 (= 14).
W tym momencie mamy już 16 cyfr. Taki system liczbowy nazywamy szesnastkowym (heksadecymalnym) lub w skrócie hex. Zamiana reprezentacji liczby między systemem binarnym a szesnastkowym jest bardzo prosta. To wyjaśnia, dlaczego system szesnastkowy jest bardzo powszechnie stosowany wtedy, gdy chcemy zapisać poza komputerem dużą liczbę binarną.
Oto kompletna tablica liczb 4-bitowych i ich szesnastkowych odpowiedników:
| zapis binarny | kod szesnastkowy |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Przykład: Największą liczbą 8-bitową jest 11111111. Można ją zapisać jako FF. Można sprawdzić, że w systemie dziesiątkowym jest to 255.
To, jakiego zapisu liczby należy użyć, zależy od konkretnej sytuacji. Reprezentacja binarna jest reprezentacją maszynową, ale jest nieodpowiednia dla człowieka. Zapis szesnastkowy to dobry sposób na skrócenie zapisu binarnego. Zapis dziesiątkowy jest używany wtedy, gdy człowiek wykonuje zwykłe obliczenia. Wszystkie trzy notacje są używane w informatyce.
Trzeba podkreślić, że w komputerach stosuje się wyłącznie binarny zapis liczb. W pamięci komputerowej nie jest możliwe zapisanie liczb bezpośrednio w systemie dziesiątkowym lub szesnastkowym.
Dane liczbowe przetwarzamy zwykle pracując z arkuszem kalkulacyjnym lub bazą danych. Dane źródłowe do przetwarzania można wprowadzać do programu komputerowego bezpośrednio z klawiatury, z pliku utworzonego przez innych program lub za pośrednictwem różnych czujników, np. temperatury, ciśnienia powietrza, czy drgań mechanicznych.
Trzeba zaznaczyć, że nie wszystkie informacje liczbowe, są zapisywane w komputerze jako liczby, a jako ciągi znaków, np. numer telefonu (61) 55-123-456. Z drugiej strony informacje, które na pierwszy rzut oka nie są liczbami (np. „30 stycznia 2014”), mogą być ku naszemu zaskoczeniu zapisywane przez oprogramowanie jako liczby (co pozwala np. w programie Excel na odejmowanie jednej daty od drugiej, w celu wyznaczenia liczby dni pomiędzy dwoma wydarzeniami). Rolą oprogramowania jest wyświetlenie liczby w odpowiedni sposób dla użytkownika, w zalezności od jej interpretacji w konkretnej sytuacji.
-
Ciekawostka. Więcej na temat zapisu danych
W arkuszu kalkulacyjnym Excel próba wykonania odejmowania jednej daty od drugiej skończy się wyznaczeniem liczby dni dzielących te dwie daty. Pojedyncza data natomiast jest w istocie zapisywana w pamięci jako liczba dni, które minęły od 1 stycznia 1900 roku.
Wszelkie typy danych zapisuje się dziś w komputerach cyfrowo, tzn. jako liczby zakodowane binarnie.
Z tematem zapisu liczb w komputerze wiążą się pytania:
- Jaki zakres liczb można zapisać w praktyce?
- Jak zapisywać liczby ujemne?
- Jak zapisywać liczby niecałkowite?
W praktyce wygląda to tak, że w pamięci komputera trzeba zarezerwować konkretną liczbę bitów jeszcze zanim będzie znana liczba, którą chcemy w pamięci zapisać. Dzisiaj często rezerwuje się 32 bity lub 64 bity, choć czasem, w uzasadnionych przypadkach, może to być 16 bitów lub nawet 128 bitów.
W każdym systemie komputerowym trzeba przyjąć pewne kompromisowe rozwiązanie pomiędzy liczbą bitów rezerwowanych w pamięci a zakresem liczb, które w taki sposób można zapisać.
Niektóre narzędzia (języki programowania czy systemy baz danych) pozwalają na wybór ilości przydzielanej pamięci spośród pewnej liczby możliwości; inne w sposób arbitralny mają to ustalone z góry (np. arkusze kalkulacyjne).
Istnieją też aplikacje, które potrafią samodzielnie w razie potrzeby zwiększyć obszar rezerwowanej pamięci (np. dla liczby całkowitej czyni tak interpreter języka programowania Python). Należy podkreślić, że zwykle będzie to wielokrotność 32 bitów (odpowiednio 32, 64, 96, 128, 160 itd.). Działa to tak, że w momencie, gdy 32 bity to zbyt mało do zapisania liczby, to komputer przenosi jej zapis do innego fragmentu pamięci o wielkości 64 bitów itp.
W niektórych językach programowania nie ma automatycznej kontroli, która pozwoliłaby stwierdzić, że nastąpiła próba zapisu zbyt dużej liczby spoza zakresu (przepełnienie). Przykład: Dodanie 1 do liczby 127 w przypadku zapisu 8-bitowego zakończy się takim zapisem binanrym, który będzie interpretowany jako −128. Innym przykładem jest tzw. problem roku 2038. Okazuje się, że 19 stycznia 2038 roku nastąpi błąd przepełnienia i błędnie będzie interpretowana data w oprogramowaniu, które datę zapisuje jako liczbę 32-bitową. Z dość podobnym problemem mieliśmy do czynienia w roku 2000.
W komputerach małych rozmiarów, takich jak np. te wbudowane wewnątrz samochodu, zmywarki, czy w czujnikach o rozmiarach wielkości ziarnka piasku, może być konieczne bardziej precyzyjne określenie zakresu przewarzanych liczb. W przypadku zwyczajnych komputerów standardem jest przetwarzanie bloków 32 bitowych jako niepodzielnej liczby bitów. Jednak czasami (np. w oprogramowaniu czujnika wstrząsów sejsmicznych) może być konieczne zastosowanie podziału: 7 bitów do zapisu szerokości geograficznej, następne 7 bitów do zapisu długości geograficznej, kolejne 10 bitów do zapisania informacji o głębokości pod powierznią ziemi, a 8 bitów dla informacji o sile wstrząsu.
Nawet podczas pracy ze standardowym komputerem jest ważne, aby starannie określić liczbę potrzebnych bitów. Na przykład, jeśli w bazie danych konkretne pole ma przyjmować jedną z czterech wartości (np. 0, 1, 2, 3 dla wartości składowych sekwencji DNA), to rezerwowanie 64 bitów do zapisania takiej wartości niepotrzebnie powiększa rozmiar bazy danych (zapisanej na dysku). Gdyby liczba rekordów bazy danych była równa 10 000 000, to w konsekwencji zmarnowanych byłoby 620 000 000 bitów, czyli ok. 74 MB, gdyż do zapisu czterech różnych wartości wystarczą 2 bity. Jeśli podobnych pól w bazie danych jest więcej, to efekt marnowania pamięci komputera kumuluje się do ogromnych rozmiarów.
Systemy oprogramowania takie jak Google Maps przetwarzają astronomiczne ilości danych i nie mogą sobie pozwolić na marnotrawienie zasobów pamięci!
-
Wyzwanie. Ile bitów jest niezbędnych?
Czymś bardzo użytecznym jest oszacowanie liczby bitów niezbędnych do zapamiętania pewnych wartości. Zastanów się, jaka byłaby odpowiedź dla sytuacji przedstawionych poniżej. Pamiętaj, że chcesz mieć możliwość zapamiętania największej z potencjalnych wartości, ale nie chcesz marnować pamięci komputera.
- Informacja o dniu tygodnia: a) 1 bit? b) 4 bity? c) 8 bitów? d) 32 bity?
- Informacja o liczbie ludzi na świecie: a) 16 bitów? b) 32 bity? c) 64 bity? d) 128 bitów?
- Informacja o liczbie dróg w Polsce: a) 16 bitów? b) 32 bity? c) 64 bity? d) 128 bitów?
- Informacja o liczbie gwiazd we wszechświecie: a) 16 bitów? b) 32 bity? c) 64 bity? d) 128 bitów?
-
Spojler. Odpowiedzi
- b)
Dodajmy, że właściwie już 3 bity pozwolą na zapis 8 różnych wartości. Jednak w praktyce na dane tej wielkości rezerwuje się w systemie 4 bity, bo -- z przyczyn technicznych -- komputer łatwiej operuje na 4 bitach niż na 3 (nie wnikając w szczegóły, chodzi o to, że bajt da się podzielić na dwie grupy po 4 bity). - c)
32 bity to za mało. - c)
To było trudne pytanie, ale projektujący bazę danych musi i o takich rzeczach myśleć. W Polsce jest łącznie ok. 420 000 km dróg i założenie, że średnia długość drogi to przynajmniej 1 km prowadzi do wniosku, że 16 bitów to za mało. Bezpieczniejszą opcją wydają się 32 bity. - d)
64 bity to za mało, a 128 bitów to o wiele za dużo! Trzeba pamiętać, że największa liczba 128-bitowa nie jest dwa razy większa niż największa liczba 64-bitowa.
- b)
Sposób zapisu liczb przedstawiony do tej pory umożliwiał zapis tylko liczb nieujemnych. W praktyce często potrzebujemy również zapisywać informacje o wartościach ujemnych (np. o obciążeniu rachunku bankowego czy temperaturze powietrza zimą!). Kiedy posługujemy się zapisem dziesiątkowym, liczbę ujemną uzyskujemy poprzez dopisanie znaku minus przed liczbą. W komputerze nie ma takiej możliwości.
Przyjrzymy się dwóm możliwym rozwiązaniom: dodanie bitu znaku (metoda podobna do używanej przez człowieka w zapisie dziesiątkowym) i zastosowanie kodu uzupełnień do 2 (metoda o wiele bardziej użyteczna w przypadku komputerów).
W komputerze nie ma możliwości dopisania znaku − (minus) przed liczbą, ale możemy przydzielić jeden dodatkowy bit, zwany bitem znaku. To może być skrajny lewy bit bajtu – gdy ustawimy go na „0”, to uznamy liczbę za dodatnią, a w przypadku „1” liczba będzie ujemna (jest to analogia do znaku minus).
Przykład: W reprezentacji 8-bitowej ze znakiem liczba 41 będzie zapisana jako 00101001, gdzie pierwszy bit (0) to bit znaku, a kolejne bity to zapis binarny liczby 41 na 7 bitach. Podobnie liczba −59 będzie mieć reprezentację 10111011, gdzie pierwszy bit (1) jest bitem znaku, a kolejne bity to liczba 59 zapisana binarnie.
-
Ciekawostka. Zapis liczb ujemnych (metoda znak-moduł)
Znajdź 8-bitową reprezentację binarną liczb: 1, −1, −8, 34, −37, −88 i 102. Jakie liczby będą reprezentowane jako 10000110, 01111111 i 10000000 w przypadku systemu 8-bitowego?
-
Spojler. Odpowiedzi
W poniższych odpowiedziach dodaliśmy odstępy dla ułatwienia czytania liczb binarnych.
- 1 to 0000 0001
- −1 to 1000 0001
- −8 to 1000 1000
- 34 to 0010 0010
- −37 to 1010 0101
- −88 to 1101 1000
- 102 to 0110 0110
Dekodowanie, czyli określenie wartości dziesiętnej na podstawie zapisu binarnego jest proste. Liczba zapisana jako 1001 0111 to na pewno liczba ujemna. Po bicie znaku (1) mamy 7 bitów 001 0111 reprezentujących 23. Stąd wartość szukana to −23.
-
Wyzwanie. Zapis dziesiątkowy liczb biarnych ze znakiem
Jakie liczby będą reprezentowane jako 0001 0011, 1000 0110, 10100011, 0111 1111 i 11111111 w przypadku systemu 8-bitowego?
- 00010011
- 10000110
- 10100011
- 01111111
- 11111111
-
Spojler. Odpowiedzi
- 0001 0011 to 19
- 1000 0110 to −6
- 1010 0011 to −35
- 0111 1111 to 127
- 1111 1111 to −127
Jakiej liczbie dziesiętnej odpowiada 1000 0000? Odpowiedź to: −0. A 0000 0000? To jest +0. Przykład 1000 0000 jest dobrą ilustracją jednej z wad, jaką ma wyżej opisany sposób zapisu. Liczba 0 ma dwie reprezentacje: −0 i +0. To nie tylko rozrzutność, ale przede wszytkim źródło potencjalnego zamieszania. W praktyce tej metody nie używa się. Komputery używają bardziej wyrafinowanej metody opisanej poniżej.
Istnieje inny sposób zapisu liczb ujemnych zwany kodem uzupełnień do 2, który nie tylko pozbawiony jest wyżej opisanej wady, ale znacznie ułatwia operacje arytmetyczne na liczbach ujemnych. Jedną z jego zalet jest ujednolicenie arytmetyki (działania wykonywane z liczbą ujemną nie muszą być traktowane jako odrębny przypadek), co daje zysk szybkości oraz upraszcza projektowanie cyfrowych układów arymetycznych (sumatorów).
Zapis liczb dodatnich w kodzie U2
Liczby dodatnie zapisuje się dokładnie w ten sam sposób, jak to było przedstawione w poprzednich rozdziałach. W przypadku zapisu 8-bitowego lewy skrajny bit jest ustawiony na 0, a pozostałe 7 bitów przeznacza się na zapis wartości liczby; na przykład 1 zapiszmy jako 00000001, a 65 jako 00110010.
Zapis liczb ujemnych w kodzie U2
Ten przypadek jest trudniejszy. Proces konwersji (zamiany z systemu dziesiętnego na binarny) można opisać taką listą kroków:
- Zapisz binarnie wartość bezwzględną liczby (czyli bez znaku minus).
- Zmień wartości wszystkich bitów na przeciwne (tj. zmień 0 na 1, a 1 na 0).
- Powiększ liczbę o 1 (dodanie 1 w arytmetyce binarnej jest dość proste; poniżej znajdzisz pewne wskazówki).
Na przykład dla −118 kolejne kroki będą wyglądać tak:
- Zapis binarny liczby 118 to 01110110
- 01110110 po zamianie wartości bitów to 10001001
- 10001001 + 1 jest równe 10001010
Stąd zapis liczby −118 w kodzie uzupełnieniowym (U2) to: 10001010.
-
Wyzwanie. Dodanie 1 w arytmetyce binarnej
Reguła rządząca dodaniem 1 w arytmetyce binarnej jest bardzo prosta, więc warto ją odkryć samodzielnie. Po pierwsze: Jeśli zapis binarny liczby kończy się 0 (np. 1101010), to jaki będzie efekt zamiany ostatniego 0 na 1? Rozpatrz inne przypadki: Jeśli zapis kończy się bitami 01, to o ile większa będzie liczba jeśli w tych miejscach wpiszemy 10? Co w przypadku zapisów kończących się 011 czy 011111?
Te proste reguły oznaczają w praktyce, że upraszcza się projektowanie sumatorów (cyfrowych układów elektronicznych, wykonujących dodawanie).
-
Dla nauczyciela. Dodanie 1 w arytmetyce binarnej
Uczniowie powinni samodzielnie, przez wykonanie kilku przykładów, odkryć regułę dodawania 1 do liczby zapisanej binarnie.
Istnieją różne sposoby mówienia o tym procesie. Regułę można wyrazić takimi słowami: Zacznij od skrajnej prawej cyfry. Zmień wartości kolejnych bitów na przeciwne tak długo aż pierwszy raz zmienisz 0 na 1.
Reguła może być sformułowana inaczej: Znajdź cyfrę 0 położoną najbardziej na prawo, zmień ją na 1, a wszystkie jedynki po prawej zmień na 0. Jak to będzie działać dla przykładu 10010111? Otrzymamy 10011000.
Gdy w liczbie zera nie występują (np. 1111111), można dopisać 0 na początku (01111111). Zastosowanie reguły da odpowiedź: 10000000.
Być może warto, aby uczniowie poszukali analogicznej reguły dotyczącej zapisu dziesiętnego: jak dodać 1 do 284 394? To 38 999? 9 999 799?
-
Wyzwanie. Zapisywanie liczb w kodzie U2
Zapisz poniższe liczby w kodzie U2, używając 8 bitów.
- 19
- −19
- 107
- −107
- −92
-
Spojler. Odpowiedzi
- 19 ma kod 0001 0011.
- Dla −19, zaczynamy od zapisania kodu dla 19, czyli 0001 0011, po zamianie bitów mamy 1110 1100, a po dodaniu 1 otrzymujemy poszukiwany kod: 1110 1101.
- 107 ma kod 0110 1011.
- Dla −107 mamy kolejno (jako etapy pośrednie): 0110 1011 i 1001 0100, a ostatecznie: 1001 0101.
- Dla −92 mamy: 0101 1100, 1010 0011 i w końcu 1010 0100.
Konwersja liczby binarnej z kodu U2 na zapis dziesiątkowy
Aby dokonać konwersji w odwrotną stronę (z reprezentacji binarnej na dziesiętną) trzeba najpierw określić, czy liczba jest dodatnia (lub równa 0), czy ujemna. Jeśli liczba jest nieujemna, to jej reprezentacji dziesiętnej szukamy w znany już sposób. W przeciwnym wypadku zaczynamy od konwersji liczby z kodu U2 do naturalnej postaci binarnej wartości bezwględnej liczby (bez znaku).
Skąd wiadomo, czy liczba jest ujemna czy nie? Wystarczy sprawdzić, czy skrajny lewy bit jest ustawiony na 1, czy 0. W pierwszym przypadku liczba jest ujemna. To wynika z opisu kodu U2 zawartego w poprzednim podrozdziale.
Jeśli zapis binarny liczby zaczyna się od 1, to proces konwersji na postać dziesiętną można przedstawić jako taką listę kroków:
- Odejmij 1 (w arytmetyce binarnej).
- Zmień wartości wszystkich bitów na przeciwne.
- Znajdź postać dziesiętną liczby uzyskanej w kroku 2.
- Dopisz znak − (minus) przed wartością wyznaczoną w kroku 3.
Na przykład dla liczby 11100010 kolejne kroki dają takie efekty:
- 11100001
- 00011110
- 30
- −30
-
Wyzwanie. U2 a zapis dziesiątkowy
Zapisz w postaci dziesiętnej liczby zapisane w kodzie U2:
- 00001100
- 10001100
- 10111111
-
Spojler. Odpowiedzi
- 12
- 10001100 -> 10001011 -> 01110100 -> 116 -> −116
- 10111111 -> 10111110 -> 01000001 -> 65 -> −65
Ile liczb można zapisać w kodzie U2?
Wiadomo już, że na 8 bitach można zapisać 256 różnych liczb. W przypadku kodu U2 największą możliwą liczbą nie będzie 255. Trzeba pamiętać, że skrajny lewy bit to bit znaku!
W praktyce można zapisać liczby z zakresów podanych w tabeli.
Wynika to wprost z faktu, że dla 8 bitów w kodzie naturalnym najmniejsza liczba ma kod 00000000, a największa -- 11111111. W kodzie uzupełnienowym (U2) wygląda to inaczej: 10000000 (kod najmniejszej liczby) i 01111111 (kod największej liczby).
| liczba bitów | zakres liczb w kodzie naturalnym | zakres liczb w kodzie U2 |
|---|---|---|
| 8 bit | od 0 do 255 | od −128 do 127 |
| 16 bit | od 0 do 65 535 | od −32 768 do 32 767 |
| 32 bit | od 0 do 4 294 967 295 | od −2 147 483 648 do 2 147 483 647 |
| 64 bit | od 0 do 18 446 744 073 709 551 615 | od −9 223 372 036 854 775 808 do 9 223 372 036 854 775 807 |
Spójrzmy najpierw na dodawanie liczb dodatnich. Reguły są analogiczne do tych znanych z pisemnego sposobu dodowania liczb w systemie dziesiątkowym. Jest przy tym prościej: są tylko dwa rodziaje cyfr, więc upraszcza się tabliczka dodawania!
Sposób pisemnego dodawania przypomnimy na przykładzie 128 + 255.
1 (przeniesienie)
128
+255
----
383
Zauważmy, że wynik dodawania 5 + 8 jest liczbą większą od 9. Dlatego na pozycji jedności w wyniku zapisujemy 3, a 10 (= 13 − 3) stanowi jedną dziesiątkę, więc mówimy o przeniesieniu (dodatkowy składnik w kolumnie dziesiątek). Dodawanie w systemie binarnym realizuje się w analogiczny sposób.
Dodawanie liczb dodatnich
Chcąc wykonać dodawanie dwóch liczb, np. 00001111 i 11001110, należy się posłużyć sposobem pisemnym dodawania (w kolumnach). W przypadku systemu binarnego wszystkie reguły, jaki trzeba znać dotyczą działań: 0 + 0, 0 + 1, 1 + 0, 1 + 1 oraz 1 + 1 + 1. Wyniki pierwszych trzech dodawań są oczywiste. Dodawanie 1 + 1 kończy się przeniesieniem, gdyż 1+1=10 (binarnie). W zapisie sposobem pisemnym oznacza to zapisanie 0 jako wyniku częściowego i przeniesienie 1 do kolumny z lewej (o ile istnieje). Ostatnie dodawanie, 1+1+1 daje sumę 11 (binarnie), co oznacza zapisanie 1 jako wyniku częściowego i przeniesienie 1 do kolumny z lewej (o ile istnieje). Oto przykład:
111 (przeniesienie)
11001110
+00001111
---------
11011101
Trzeba pamiętać, że w zapisie binarnym używa się wyłącznie cyfr 1 i 0. To oznacza konieczność przeniesienia 1 do kolumny na wyższej pozycji (z lewej), gdy suma częściowa jest równa 2 lub 3 (dziesiętnie).
Dodawanie liczb ujemnych w kodzie moduł-znak
W przypadku liczb ujemnych zapisanych w kodzie moduł-znak (czyli z lewym skrajnym bitem jako bitem znaku), metoda opisana wyżej nie zadziała. Dla przykładu dodanie +11 (01011) do −7 (10111) powinno zakończyć się wynikiem +4 (00100).
11111 (przeniesienie)
01011
+10111
100010
Wynikiem jest jednak liczba −2.
Jak można ten problem rozwiązać? Okazuje się, że zamiast dodawnia kolumn można by użyć odejmowania kolumn. Jednak w praktyce wymagałoby to użycia specjalnego układu elektronicznego. Na szczęście jest inne rozwiązanie: z pomocą przychodzi kod uzupełnieniowy (U2)!
Dodawanie liczb ujemnych w kodzie U2
Dla przykładu (+11 + −7) należy rozpocząć od zapisania składników w kodzie U2 na 5 bitach. Otrzymujemy: 01011 (+11) i 11001 (−7).
Dodawanie w kolumnach zapiszemy tak:
01011
11001
100100
Dodatkowy szósty bit (po lewej) powstały z przeniesienia należy zignorować. Pozostałe 5 bitów to 00100, czyli 4. Takiego wyniku oczekiwaliśmy.
Opisaną wyżej metodę można zaadaptować do odejmowania: zamiast działania 5 − 2, należy wykonać wykonać działanie 5 + (−2) = 3.
Własności kodowania U2 są bardzo użyteczne. Dzięki temu można wykonywać działania zarówno na liczbach ujemnych, jak i nieujemnych za pomocą tych samych elektronicznych układów arytmetycznych, a dodawanie i odejmowanie można potraktować jako ten sam typ operacji arytmetycznej.
-
Dla ciekawych. O co chodzi z kodeum U2?
Pomysł wykonywania dodawania na tzw. dopełnieniu liczby zamiast odejmowania liczby można zastosować w obliczeniach na liczbach dziesiętnych. Dopełnieniem dziesiętnym x jest 10 − x, np. dla 4 to 6, a dla 8 to 2. (Słowo „dopełnić” ma ten sam rdzeń, co słowo pełnia. Liczba 10 jest w tym przypadku taką pełną, „okrągłą” liczbą.)
Odejmowanie 2 od 6 jest tożsame z dodawaniem 8 do 6 (6 + 8 = 14) i ignorowaniem 1 z przeniesienia (po lewej).
Dla większych liczb (np. trzycyfrowych) dopełnieniem liczby jest liczba, która stanowi różnicę brakującą do kolejnej potęgi 10, tj. 1000 − 128 = 872.
W przypadku zapisu binarnego sytuacja jest prostsza, bo używa się tylko dwóch różnych cyfr. Porównanie z systemem dziesiątkowym może być jednak pomocne dla zrozumienia tematu.
Przedstawiliśmy dwa różne sposoby zapisu liczb ujemnych na komputerze. W praktyce pierwszy sposób (moduł-znak) jest rzadko używany. Jego wadami jest to, że liczba 0 ma w nim dwie reprezentacje oraz konieczność stosowania odrębnych układów logicznych (sumatorów) dla liczb dodatnich i ujemnych. Drugi sposób (kod uzupełnień do 2) jest powszechnie w użyciu, gdyż pozbawiony jest wad pierwszego rozwiązania, tj. liczba 0 ma jedną reprezentację, a odejmowanie można w prosty sposób zastąpić dodawaniem.
Istnieją jeszcze inne sposoby kodowania liczb ujemnych (np. uzupłenienie do 1, kodowanie z przesunięciem), ale metoda U2 jest najbardziej powszechna.
Istnieje kilka różnych sposobów używanych przez komputery do zapisywania znaków i tekstów. W tym rozdziale przyjrzymy się najczęściej stosowanym. Opiszemy zalety i wady każdej z metod.
W jednym z poprzednich podrozdziałów stwierdziliśmy, że sześć punktów systemu Braille'a pozwala uzyskać 64 różne wzorce (znaki).
Spróbuj policzyć, ile różnych wielkich liter, małych liter, liczb i innych znaków możesz wprowadzić do edytora tekstu, używając klawiatury komputerowej. (Nie zapomnij o znakach, które współdzielą klawisze z cyframi i o znakach interpunkcyjnych!)
-
Co to jest?. Znaki
Wspólną nazwą dla wielkich i małych liter, liczb i symboli jest znak (ang. character). Na przykład a, D, 1, h, 6, *, ], jak również ~ (tylda), wszystkie są znakami. Należy podkreślić, że spacja (odstęp) jest również znakiem.
Jeśli ktoś dokładnie policzył, to wie, że znaków jest więcej niż 64, bo ponad 90. Użycie 6 bitów nie wystarczy, by zapisać wszystkie znaki. Okazuje się, że potrzeba przynajmniej 7 bitów. Dokładnie tyle zastosowano w oryginalnej wersji kodowania ASCII.
-
Wyzwanie. Dlaczego 7 bitów?
Przy omawianiu kodu Braille'a wyjaśniliśmy, co dzieje się po zwiększeniu liczby punktów o 1 (pamiętaj, że kod Braille'a jest kodem binarnym). Możesz wyjaśnić, skąd wiadomo, że 6 bitów wystarczy do zapisu 64 znaków, a 7 bitów umożliwia zapis nawet 128 znaków?
Koncepcją zastosowaną w ASCII było przypisanie różnych wzorców bitowych każdemu ze znaków stosowanych w tekstach angielskich (oraz pewnej liczbie tzw. znaków sterujących, używanych dawniej w aparatach dalekopisowych – dziś tylko niektóre z nich mają zastosowanie w technice komputerowej, ale ten wątek pominiemy). W dzisiejszej postaci kodu ASCII dla języka angielskiego stosuje się wzorce 8-bitowe (bajty), w których pierwszy bit ma zawsze wartość 0, co znaczy, że kod umożliwia zapis 128 znaków.
W tabeli przedstawiono zestawienie znaków i odpowiadajacych im wzorców 7-bitowych w kodzie ASCII:
| postać binarna | znak | postać binarna | znak | postać binarna | znak | |
|---|---|---|---|---|---|---|
| 0100000 | spacja | 1000000 | @ | 1100000 | ` | |
| 0100001 | ! | 1000001 | A | 1100001 | a | |
| 0100010 | " | 1000010 | B | 1100010 | b | |
| 0100011 | # | 1000011 | C | 1100011 | c | |
| 0100100 | $ | 1000100 | D | 1100100 | d | |
| 0100101 | % | 1000101 | E | 1100101 | e | |
| 0100110 | & | 1000110 | F | 1100110 | f | |
| 0100111 | ' | 1000111 | G | 1100111 | g | |
| 0101000 | ( | 1001000 | H | 1101000 | h | |
| 0101001 | ) | 1001001 | I | 1101001 | i | |
| 0101010 | * | 1001010 | J | 1101010 | j | |
| 0101011 | + | 1001011 | K | 1101011 | k | |
| 0101100 | , | 1001100 | L | 1101100 | l | |
| 0101101 | - | 1001101 | M | 1101101 | m | |
| 0101110 | . | 1001110 | N | 1101110 | n | |
| 0101111 | / | 1001111 | O | 1101111 | o | |
| 0110000 | 0 | 1010000 | P | 1110000 | p | |
| 0110001 | 1 | 1010001 | Q | 1110001 | q | |
| 0110010 | 2 | 1010010 | R | 1110010 | r | |
| 0110011 | 3 | 1010011 | S | 1110011 | s | |
| 0110100 | 4 | 1010100 | T | 1110100 | t | |
| 0110101 | 5 | 1010101 | U | 1110101 | u | |
| 0110110 | 6 | 1010110 | V | 1110110 | v | |
| 0110111 | 7 | 1010111 | W | 1110111 | w | |
| 0111000 | 8 | 1011000 | X | 1111000 | x | |
| 0111001 | 9 | 1011001 | Y | 1111001 | y | |
| 0111010 | : | 1011010 | Z | 1111010 | z | |
| 0111011 | ; | 1011011 | [ | 1111011 | { | |
| 0111100 | < | 1011100 | \ | 1111100 | \ | |
| 0111101 | = | 1011101 | ] | 1111101 | } | |
| 0111110 | > | 1011110 | ^ | 1111110 | ~ | |
| 0111111 | ? | 1011111 | _ | 1111111 | Delete |
Przykład: Litera c (mała litera) ma w tabeli przypisany wzorzec 01100011 (0 na początku jest dopełnieniem kodu do 8 bitów). Litera o ma wzorzec 01101111. Warto w ramach ćwiczenia zapisać jakieś słowo, używając kodu ASCII i dać komuś innemu, kto również zapoznaje się z tym tematem, do odkodowania.
-
Dla nauczyciela. Jak stosować tablicę ASCII?
Należy polecić uczniom wymianę krótkich wiadomości zapisanych w kodzie ASCII. Wtedy będą mieli okazję dostrzec pewne prawidłowości, wzorce (np. wielkie litery różnią się od odpowiadających im małych liter tylko na jednym bicie).
W komputerach teksty w języku angielskim są zapisywane w postaci ciągów (sekwencji) wzorców 8-bitowych, bardzo podobnie jak to było z zapisem w Braille'u. Dla przykładu słowo computers będzie zapisane jako: 01100011 01101111 01101101 01110000 01110101 01110100 01100101 01110010 01110011. Litera c ma kod 01100011, litera o ma kod 01101111 itd. Spójrz do tablicy ASCII, aby to sprawdzić!
-
Ciekawostka. Co oznacza skrót ASCII?
Nazwa ASCII jest skrótem od American Standard Code for Information Interchange. Była to standaryzacja sposobu kodowania znaków w maszynie dalekopisowej (zautomatyzowanym systemie telegraficznym). Dlatego system ASCII zawiera także znaki dla sygnału dzwonka, dla informacji o potrzebie usunięcia poprzedniego znaku (jakby przodek polecenia „cofnij”), czy dla potwierdzenia zakończenia transmisji (END). We fragmencie tabeli ASCII, zamieszczonym powyżej, znajdziesz tylko jeden z nich (DEL). Resztę pominięto.
Dzisiaj system ASCII został wyparty przez kodowanie UTF-8. Należy podkreślić, że teksty angielskie zakodowane w UTF-8 mają identyczną reprezentację binarną, co teksty w ASCII, gdyż pierwszy bit każdego 8-bitowego wzorca jest wówczas równy 0. Inaczej mówiąc plik tekstowy zawierający wzorce 1xxxxxxx z całą pewnością nie jest zapisany w kodzie ASCII i zawiera informacje o znakach spoza alfabetu angielskiego.
-
Wyzwanie. Więcej o ASCII
Odpowiedz na następujące pytania:
Jak zapisać słowo science, używając kodu ASCII? A słowo Wellington (zauważ, że słowo rozpoczyna się wielką literą W)? Jak zapisać 358 (czyli ciąg trzech cyfr)? Zapisz całe zdanie: „Hello, how are you?” (odszukaj w tabeli kodów ASCII wzorca dla przecinka, znaku zapytania i spacji).
-
Spojler. Odpowiedzi
Oto odpowiedzi:
- science to 01110011 01100011 01101001 01100101 01101110 01100011 01100101
- Wellington to 01010111 01100101 01101100 01101100 01101001 01101110 01100111 01110100 01101111 01101110
- 358 to 00110011 00110101 00111000
Zauważ, że ciąg znaków 358 (w kodzie ASCII) można pomylić z liczbą 358. Z taką sytuacją możesz spotkać się np. w arkuszu kalkulacyjnym. Warto wiedzieć, że poprzedzenie pierwszej cyfry znakiem ' niejako wymusza, by arkusz traktował cyfry jako znaki tekstu, a nie liczby. To jest istotne np. gdy chcemy zapisać numer telefonu. Domyślnie 061555555 przez artkusz będzie potraktowane jako 61555555 (pominięte będzie 0).
Kod ASCII jest stosowany w technice komputerowej i telekomunikacji już od roku 1963. Pomimo wielkich zmian w konstrukcji komputerów i systemów operacyjnych, kodowanie ASCII jest ciągle podstawą komputerowych systemów zapisu tekstu w języku angielskim.
Dla tekstów w języku angielskim kod ASCII jest wystarczającym rozwiązaniem. Co jednak zrobić w przypadku języków takich jak chiński, w których stosuje się tysiące różnych znaków? 128 kombinacji zerojedynkowych to za mało! ASCII dzisiaj nie jest już powszechnie stosowany. Używa się rozwiązania zwanego Unicode.
-
Ciekawostka. Co było przed ASCII?
Warto wspomnieć, że zanim pojawił się standard ASCII w usługach telegraficznych stosowano inne standardy: kod Baudota i EBCDIC. Powszechnie stosowana była odmiana kodu o nazwie kod Baudota-Murraya. Jej autorem był Donald Murray, urodzony w Nowej Zelandii. Jednym z elementów kodu było wprowadzenie „kodów kontrolnych”, takich jak kod powrotu karerki i nowej linii. Zauważ, że przycisk CONTROL (CTRL) nadal jest elementem klawiatury.
Dzisiaj standardem, który umożliwia zapis liter spoza alfabetu angielskiego, jest Unicode. To tablica kodowa, w której znajdziemy ok. 120 000 różnych znaków, właściwych dla różnych języków, współczesnych i martywch.
Uzyskanie konkretnego binarnego kodu znaku w Unicode wymaga użycia schematu kodowania (ang. encoding scheme).
Dzięki poniższej aplikacji zaznajomisz się ze szczegółami. Po wpisaniu liczby w polu po lewej, zobaczysz odpowiadający mu znak. Po wpisaniu znaku w polu po prawej, zobaczysz liczbę Unicode (warto sprawdzić znak spoza angielskiego alfabetu).
Znaki Unicode
Najbardziej popularne sposoby kodowania Unicode to UTF-8, UTF-16, and UTF-32; takie skróty można czasem zobaczyć w nagłówkach emaili lub opisach właściwości plików tekstowych. Część sposobów to kodowania o stałej długości (liczbie bitów np. 32), a inne są zmiennej długości. W tym drugim przypadku znaki powszechnie używane zapisuje się z użyciem mniejszej liczby bitów (np. 1 bajta), co daje oszczędność. Istnienie wielu schematów kodowania wynika z tego, że nie ma jednego najlepszego dla wszystkich języków.
UTF-32 jest sposobem kodowania Unicode o stałej długości. Kod każdego znaku to liczba 32-bitowa. Oznacza to, że właściwy kod znaku poprzedza odpowiednia liczba zer (dopełniająca liczbę bitów do 32). To tak jak czterocyfrowy zapis liczby 254 -- 0254. 32 bity określa się czasem jako słowo maszynowe (w architekturze komputera), więc można powiedzieć, że to tzw. okrągła liczba.
Na przykład znak H w schemacie UTF-32 to:
00000000 00000000 00000000 01001000
Znak $ w schemacie UTF-32 to:
00000000 00000000 00000000 00100100
Polski znak ł w schemacie UTF-32 to:
00000000 00000000 00000001 01000010
A znak 犬 w schemacie UTF-32 to:
00000000 00000000 01110010 10101100
Poniżej znajduje się aplikacja, umożliwiająca wyznaczenie kodu Unicode znaku w schemacie UTF-32.
-
Projekt. Imię w kodzie UTF-32
- Znajdź kody liter twojego imienia w schemacie UTF-32.
- Sprawdź, ile bitów zajmuje właściwy kod litery, a ile bitów to zera uzupełniające zapis binarny do 32 bitów.
- Wyjaśnij, na czym polega binarny zapis danego znaku tekstu (według kodu Unicode).
W kodzie ASCII stosuje się właściwie identyczne podejście. Każdy znak ma kod binarny, który zapisany dziesiętnie jest liczbą z zakresu 0 -- 255. ASCII jest także kodowaniem o ustalonej długości -- każdy znak w ASCII jest kodowany z użyciem 8 bitów.
W praktyce schemat UTF-32 jest rzadko używany -- własnie dlatego, że wiąże się z marnotrawieniem zasobów. Schematy UTF-8 i UTF-16 są zmiennej długości, są powszechnie używane. Teraz się nimi zajmiemy.
-
Wyzwanie. Ile to jest 32 bity?
Jaka jest największa liczba, którą można zapisać na 32 bitach? (Odpowiedź zapisz zarówno dziesiętnie, jak i binarnie.)
Największa liczba Unicode jest daleko mniejsza od największej liczby, którą da się zapisać na 32 bitach -- ma postać 00000000 00010000 11111111 11111111. Jaką postać dziesiętną ma ta liczba?
Jaka jest najmniejsza liczba bitów, która wystarczyłaby do zapisania każdego z ok. 120 000 znaków Unicode?
-
Spojler. Odpowiedzi
4 294 967 295 (ok. 4,3 miliarda).
1 114 111.
17 bitów. 16 nie wystarczy, bo \(2^{16}\) = 65 536.
Kody binarne znaków w schemacie UTF-8 są zmiennej długości, tj. są zapisywane z użyciem 8, 16, 24, lub 32 bitów, czyli 1, 2, 3 lub 4 bajtów.
Na przykład znak H w kodzie UTF-8 to:
01001000
znak ǿ w kodzie UTF-8 to:
11000111 10111111
A znak 犬 w kodzie UTF-8 to:
11100111 10001010 10101100
Poniżej znajduje się aplikacja, dzięki której można wyznaczyć kod znaku według schematu UTF-8. Wyświetlany jest również numer znaku tablicy Unicode.
Jak działa kodowanie według schematu UTF-8? Oto instrukcja znalezienia kodu krok po kroku.
Znajdź numer Unicode dla znaku.
Zapisz numer Unicode w systemie binarnym, używając jak najmniejszej liczby bitów.
Dopasuj odpowiedni wzorzec (spośród poniższych), na podstawie liczby użytych bitów w kroku 2.
7 lub mniej bitów: 0xxxxxxx 11 lub mniej bitów: 110xxxxx 10xxxxxx 16 lub mniej bitów: 1110xxxx 10xxxxxx 10xxxxxx 21 lub mniej bitów: 11110xxx 10xxxxxx 10xxxxxx 10xxxxxxZastąp ciąg znaków x bitami z zapisu binarnego uzyskanego w kroku 2. Jeśli liczba znaków x jest większa od liczby bitów, to przed zastąpieniem znaków x cyframi, uzupełnij zapis binarny z lewej strony o odpowiednią liczbę cyfr 0.
Na przykład dla znaku 貓 (w języku chińskim oznaczającego kota) proces wyznaczania kodu wygląda tak:
- 35987
- 10001100 10010011
- Jest 16 bitów, więc używamy wzorca 1110xxxx 10xxxxxx 10xxxxx
- 11101000 10110010 10010011
Kod znaku 貓 w UTF-8 to: 11101000 10110010 10010011
Podobnie jak UTF-8, również UTF-16 jest schematem kodowania zmiennej długości. Jego budowa jest bardziej złożona niż UTF-8. Nie będziemy jej tutaj objaśniać.
Poniżej znajduje się aplikacja do zapisania tekstu w kodzie UTF-16. Możesz porównać efekty dla różnych języków (np. polskiego i japońskiego) w przypadku stosowania schematów UTF-16 i UTF-8.
Przedstawiliśmy różne metody kodowania znaków tekstu: ASCII, UTF-32, UTF-8, and UTF-16.
Poniższa tabela zbiera różne informacje na ich temat.
| kod | typ schematu | liczba bitów na znak | powszechność użycia |
|---|---|---|---|
| ASCII | stałej długości | 8 bitów | obecnie rzadziej używany |
| UTF-8 | zmiennej długości | 8, 16, 24 lub 32 bity | powszechnie używany |
| UTF-16 | zmiennej długości | 16 lub 32 bity | często używany |
| UTF-32 | stałej długości | 32 bity | rzadko używany |
Celem porównania metod kodowania, trzeba określić kryteria uznania kodowania za „dobre”. Oto dwa kryteria:
- Umożliwia zapis wszystkich znaków, niezależnie od języka.
- Do zapisu używa jak najmniejszej liczby bitów.
Kodowanie ASCII nie spełnia pierwszego kryterium. Z drugim kryterium sprawa nie jest taka prosta.
Poniżej znajduje się aplikacja, dzięki której wyznaczysz liczby bitów użytych do zapisu krótkiego tekstu w schematach: UTF-8, UTF-16 i UTF-32.
Kalkulator Unicode
Wpisz tekst, którego długość w Unicode chcesz obliczyć:
Oblicz długość (w bitach)Długość po zakodowaniu:
UTF-8: 0 bitów
UTF-16: 0 bitów
UTF-32: 0 bitów
Można powiedzieć, że UTF-8 jest lepsze dla tekstów w języku angielskim, UTF-16 dla tekstów w językach azjatyckich.
-
Ciekawostka. Emotikony i Unicode
Różne urocze małe znaki, które można używać na portalach społecznościowych itp. nazywa się emotikonami. Każdy z nich ma numer w tablicy Unicode. Najpierw emotikony pojawiły się w Japonii w wiadomościach wysyłanych z telefonów komórkowych. Dziś jest ponad 1000 różnych emotikonów. Ich listę można zobaczyć tutaj. Co ciekawe, pojedyncze znaki emoji mogą mieć różny wygląd w zależności od platformy, tj. 😆 (czyli uśmiechnięta twarz z otwartymi ustami i przymkniętymi oczami) zapisana jako element tweeta będzie wyglądać inaczej niż na iPhone'ie.
W nagraniu wideo udostępnionym poniżej ukryte są wiadomości zapisane z użyciem 5 bitów. Sprawdź, czy je znajdziesz!
Jeśli założyć, że chcemy zapisywać 26 liter angielskiego alfabetu (bez rozróżniania małych i wielkich liter), to okazuje się, że 5 bitów wystarczy.
Niech 1 odpowiada literze a, 2 -- literze b, 3 -- c, a 26 -- z. (Możesz się sam przekonać, że jeśli kody ASCII liter „obciąć” do 5 bitów mniej znaczących, to otrzymamy kody odpowiadające liczbom 1, 2, ..., 26.)
Zapisz słowo water używając opisanego wyżej schematu 5-bitowego kodowania.
-
Spojler. Odpowiedzi
w: 10111 a: 00001 t: 10111 e: 10100 r: 10010
Teraz czas na zdekodowanie wiadomości ukrytej w utworze muzycznym!
-
Dla nauczyciela. Więcej informacji o nagraniu wideo
W nagraniu wideo odnaleźć można ponad 20 ukrytych wiadomości, zawsze zapisanych z użyciem 5 bitów. Na początku mamy solo na bębnie. Pierwsze pięć dźwięków to: „tuk tuk trzask tuk tuk”. Uczniowie powinni zdecydować, który odpowiada cyfrze 0, a który cyfrze 1. Liczba zakodowana to: 00100 (d) lub 11011 (dziesiętnie to 27, co nie jest kodem żadnej litery!) Pierwsza wiadomość to „drum” (pol. bęben).
Kolejne wyzwania stają się trudniejsze (wiadomości zakodowane są również w śpiewie, ale i w tańcu oraz kolorach tła). Piosenka opowiada o steganografii. Warto, by uczniowie poszukali wyjaśnienia tego terminu.
Pewnie przypominasz sobie lekcje plastyki, na których mieszaliście farby różnych kolorów, chcąc drogą prób i błędów uzyskać inną barwę. Ile było z tym zabawy! Po wymieszaniu kolorów czerwonego i niebieskiego można było uzyskać fioletowy. Po zmieszaniu żółtłego i niebieskiego -- zielony. Czerwony w połączeniu z żółtym dawał pomarańczowy. Pewnie próbowaliście również uzyskać czarny przez zmieszanie niebieskiego, czerwonego i żółtego w równych ilościach. Zwykle efekt przypominał bardziej ciemny brąz. Mieszając farby trzech podstawowych kolorów w różnych ilościach, razem z farbą białą lub czarną, uzyskiwaliście wiele różnych, nowych kolorów.
Być może już wiesz, że w atramentowych drukarkach komputerowych też stosuje się tylko trzy podstawowe kolory. To zestaw lepszy od tego z zajęć plastycznych: turkusowy (niebieskozielony, ang. cyan), niebieskoczerwony (ang. magenta) oraz żółty (ang. yellow), określany skrótem CMY. Ten sposób mieszania barw nazywa się subtraktywnym, ponieważ można mówić o odejmowaniu (ang. subtracting, pochłanianiu niektórych długości fal przez powierzchnię). Na początku płótno, czy kartka, jest białe (czyli od powierzchni kartki odbijają się wszystkie składowe), a nałożenie farb działa jak filtr i od koloru białego odejmowane są różne składowe.
Poniżej znajduje się aplikacja, służąca lepszemu zrozumieniu modelu kolorów CMY.
Mieszacz kolorów CMY -- taki jak w drukarkach
Ekran monitora komputerowego (czy wydruk) nie zawiera informacji tylko o jednym kolorze. Obraz składa się z milionów pikseli, a kolor każdego z nich może być inny niż kolory sąsiadujących z nim pikseli.
Kolory wyświetlane na ekranach telewizorów też uzyskuje się przez zmieszanie kolorów podstawowych: czerwonego (ang. red), zielonego (ang. green) i niebieskiego (ang. blue). Mamy tu jednak do czynienia z modelem addytywnym RGB: ekran na początku jest czarny, a inne kolory uzyskuje się jakby przez dodawanie kolorów (odcieni) trzech składowych subpikseli, świecących z różną intensywnością odpowiednio: na czerwono, na zielono i na niebiesko.
Dzięki poniższej aplikacji lepiej zrozumiesz model kolorów RGB.
Mieszacz kolorów RGB -- używany do wyświetlania kolorów na ekranie
-
Spojler. Wskazówki
Ustawienie wszystkich suwaków w skrajnych pozycjach (na jednym z końców) da kolor biały lub czarny, a ustawienie ich w równej odległości od końców da odciecie szarości (tj. przejście między czarnym a białym).
Aby uzyskać kolor żółty należy zmieszać czerwony i zielony, bez niebieskiego. To może być zaskakujące.
-
Ciekawostka. Kolory podstawowe a ludzkie oko
Ludzkie oko zawiera miliony światłoczułych receptorów, zwanych czopkami. Istnieją trzy rodzaje czopków: wywołujące odpowiednio wrażenie czerwieni, wrażenie zieleni i wrażenie barwy niebieskiej. Dla przykładu: jeśli na światło reagują z podobną czułością czopki z pierwszej i trzeciej z wyżej wymienionych grup, a czopki z drugiej grupy nie reagują, to mózg postrzega tę barwę jako niebieskoczerwoną, jaśnieszą odmianę purpurowego (ang. magenta).
Kolory wyświetlane na ekranach telewizorów też uzyskuje się przez zmieszanie kolorów podstawowych: czerwonego (ang. red), zielonego (ang. green) i niebieskiego (ang. blue).
-
Co to jest?. Piksel
Słowo piksel (ang. pixel) to skrót powstały z angielskiego zwrotu picture element, czyli element obrazu. Na ekranie monitora komputerowego obraz jest siatką pikseli o różnych kolorach. Piksel ma wielkość ułamka milimetra, a więc obraz składa się zwykle z milionów pikseli (dlatego mówi się megapiksel na oznaczenie zbioru miliona pikseli).
Kluczową koncepcją zapisu informacji graficznej jest to, że kolor piksela opisuje się, używając trzech liczb (składowych). W powyższym przykładzie były to liczby od 0 do 255. Dla każdej składowej mamy wtedy 256 możliwości, co umożliwia zapis informacji o 256 x 256 x 256 = 16 777 216 różnych kolorach. To więcej, niż ludzkie oko jest w stanie rozróżnić.
Oczywiście zazwyczaj na ekranie wyświetlany jest więcej niż jeden kolor. Dzisiaj nawet ekrany komputerowe najmniejszych rozmiarów zawierają miliony pikseli i w komputerze musi być zapisana informacja o kolorze każdego z nich. Współcześnie rozmiary zdjęć mierzy się używając jednostki zwanej MP, czyli megapikselem (= milion pikseli). W systemie komputerowym informacja o kolorze każdego z pikseli zapisywana jest w postaci trzech liczb (o tym była mowa wyżej). Oznacza to, że do zapisania pełnej informacji o zdjęciu rozmiaru 2MP potrzeba sześciu milionów liczb! Mamy tu na myśli oczywiście taki sposób zapisu, w którym nie stosuje się kompresji.
Za pomocą poniższej aplikacji można powiększyć obraz tak, aby dostrzec piksele tworzące obraz. Każdy z elementów obrazu to kwadrat o jednolitym kolorze. Po odpowiednim powiększeniu wyświetlone zostaną wartości składowych RGB.
-
Dla ciekawych. Inne materiały edukacyjne
Inne ćwiczenie, które ukazuje związek między wartościami składowych RGB a wyświetlanym kolorem jest tutaj.
W jaki sposób binarnie, czyli w systemie dwójkowym, zapisać informację o kolorze, tak by obraz był wysokiej jakości? Ilu bitów potrzeba do zapisania informacji o kolorze pojedynczego piksela?
Wykonując ćwiczenie dotyczące składowych koloru (z suwakami), można było zauważyć, że suwak dla każdej składowej (czerwonej, zielonej, niebieskiej) był ustawiany w jednej z 256 pozycji (od 0 do 255). Do zapisania informacji składowej potrzeba zatem 8 bitów (ponieważ 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256).
Najmniejszą liczbą, którą można zapisać na 8 bitach jest 00000000 -- czyli 0. Największa liczba to 11111111 -- czyli 255.
Są trzy składowe, więc potrzebujemy 24 (3 x 8 = 24) bity do zapisania informacji o kolorze piksela.
Liczbę \(2^{24}\) (czyli liczbę wszystkich liczb, które można zapisać używając 24 bitów) można wyznaczyć wykonując mnożenie: 256 x 256 x 256. Otrzymujemy 16 777 216. To oznacza, że zapis 24-bitowy pozwala zachować informację o ponad 16 milionach różnych kolorów. To nam wystarczy, aby mówić o zapisie wysokiej jakości. 24-bitowy kolor nazywany bywa pełnym kolorem (ang. true color).
Jak to w praktyce wygląda? Wydaje się, że najrozsądniej jest użyć równej liczby bitów dla każdej składowej koloru. W ćwiczeniu powyżej składowe kolorów były wyświetlane jako liczby dziesiętne. Aby uzyskać binarny zapis informacji o składowych, należy zapisać te liczby w systemie dwójkowym i ustawić te 8-bitowe ciągi zer i jedynek obok siebie w odpowiedniej kolejności w jeden ciąg 24-bitowy (zgodnie z tradycyjną kolejnością: najpierw wzorzec bitowy dla składowej czerwonej, później dla zielonej, a na końcu dla niebieskiej).
Przykład: Wyobraź sobie, że składowe koloru to: czerwona = 145, zielona = 50 i niebieska = 123 (jeśli nie wierzysz, że to odcień fioletowego, możesz sam sprawdzić).
Każdą z tych trzech liczb należy napisać binarnie, używając 8 bitów. Możesz to zrobić samodzielnie (np. posługując się tzw. pianinem binarnym). Otrzymasz: czerwona = 10010001, zielona = 00110010 i niebieska = 01111011. Informacja o kolorze (odcień fioletu) będzie mieć zatem następujący wzorzec bitowy: 100100010011001001111011.
Zauważ, że nie zapisujemy odstępów między 8. i 9. bitem, ani między 16. i 17. bitem, by podkreślić, że w komputerze oczywiście nie ma miejsca na inny znak niż reprezentacja fizyczna 0 i 1 (np. niższe lub wyższe napięcie prądu). Dla wygody odczytu możesz jednak zapisywać odstępy (spacje), kiedy zapisujesz taką informację w edytorze tekstu, czy długopisem na kartce. Zwróć uwagę na to, że każda składowa opisana jest z użyciem ośmiu bitów, nawet jeśli te najbardziej znaczące ustawione są na 0. W celu lepszego zrozumienia tego zagadnienia warto zapisać kilka innych przykładów.
-
Ciekawostka. Obrazy monochromatyczne
Obrazy czarno-białe zwykle składają się z większej liczby kolorów niż dwa. Zwykle to 256 odcieni szarości, zapisane z użyciem 8 bitów.
Zapamiętaj, że odcienie szarości można uzyskać przez ustawienie tej samej wartości liczbowej dla wszystkich składowych RGB, np. 105, 105, 105. To oznacza, że wystarczy tę liczbę zapisać raz w pojedynczym bajcie.
Należy podkreślić, że komputery przetwarzają informacje zapisane binarnie, bez ich konwersji do liczb dziesiętnych. Tym przetwarzaniem zajmują się zwykle karty graficzne i drukarki. W naszych przykładach pojawiają się wartości dziesiętne wyłącznie po to, aby łatwiej je było zrozumieć.
Najważniesze jest, aby rozumieć, że cyfrowy zapis informacji o kolorze wymaga pogodzenia dwóch wyzwań: właściwego postrzegania koloru przez ludzkie oko i użycia możliwie małej liczby bitów pamieci.
-
Dla ciekawych. Szesnastkowe kody kolorów
Podczas tworzenia kodu HTML strony internetowej często trzeba określać kolor tekstu, tła itd. Można wtedy podać wprost angielską nazwę koloru, np. red, blue, purple lub gold. W ten sposób nie da się jednak opisać różnych odcieni koloru czerwonego, niebieskiego i innych. Jedynym rozwiązaniem jest wskazanie odpowiedniego kodu koloru. W praktyce nie stosuje się w tym miejscu zapisu binarnego (24 bitów), ale kody szestnastkowe, które są znacznie bardziej czytelne dla człowieka, więc pisze się np. #00FF9E. Znak # (ang. hash) to informacja dla przeglądarki internetowej, która kolejne sześć znaków zinterpretuje jako 24-bitową informację o kolorze. Takie „trójki szesnastkowe" stosuje się nie tylko w kodzie HTML, ale również np. w przypadku określania atrybutu koloru dla stylów w plikach CSS i SVG. W przykładzie używanym we wcześniejszej części tekstu pojawił się następujący wzorzec bitowy: 100100010011001001111011. Ten 24-bitowy ciąg można rozdzielić na grupy półbajtów: 1001 0001 0011 0010 0111 1011. Jeśli zastapimy każdy z nich cyfrą szesnastkową, to otrzymamy 91327B. Taki kod nazywamy kodem szesnastkowym (heksadecymalnym) koloru.
Osoba, która rozumie, na czym polega tworzenie kodów szesnastkowych, potrafi z łatwością dostosować kod koloru tak, aby uzyskać oczekiwany odcień koloru. Wiadomo, że w przypadku 24-bitowej głębi koloru, pierwsze osiem bitów (w konsekwencji pierwsze dwie cyfry szesnastkowe) określa wartość składowej czerwonej, kolejne osiem — zielonej, a ostatnie osiem — niebieskiej. Aby zwiększyć udział odpowiedniej składowej, wystarczy zmienić odpowiednio jej kod szesnastkowy. Na przykład zmiana kodu #000000 (kolor czarny) na #002300 da w efekcie odcień koloru zielonego. Jakie kolory uzyskamy, używając kodów: #FF0000, #FF00FF, #FFFFFF?
Poniżej znajduje się aplikacja do eksperymentowania z szesnastkowymi kodami koloru. Zmienia ono tło tej strony.
Zapis szesnastkowy koloru tła
Wyobraźmy sobie sytuację, w której do zapisu informacji o kolorze mamy używać mniej niż 24 bitów. Ile zyskamy? Jaki będzie mieć wpływ na jakość obrazu?
Kolejna aplikacja (poniżej) pozwala zobaczyć, jaki będzie efekt stosowania coraz mniejszej palety (głębi) kolorów, łącznie z sytuacją pominięcia informacji o kolorze (0 bitów!). Możesz wybrać obraz z menu. W którym przypadku zmiana jakości jest najbadziej dostrzegalna? W którym mniej? Kiedy należy troszczyć się o w miarę pełne zachowanie informacji o kolorach? Kiedy nie ma to większego znaczenia (tj. wystarczy nam obraz dwukolorowy)?
Można zapytać, czy zyskalibyśmy coś zapisując informację o kolorze z użyciem liczby bitów większej niż 24? Okazuje się, że ludzkie oko potrafi rozróżniać ok. 10 milionów kolorów, więc liczba kolorów dla głębi 24-bitowej (ponad 16 milionów) jest większa. Czasami jednak stosuje się więcej bitów, np. w przypadku, gdy chcemy na obrazie odzwierciedlić kontrast.
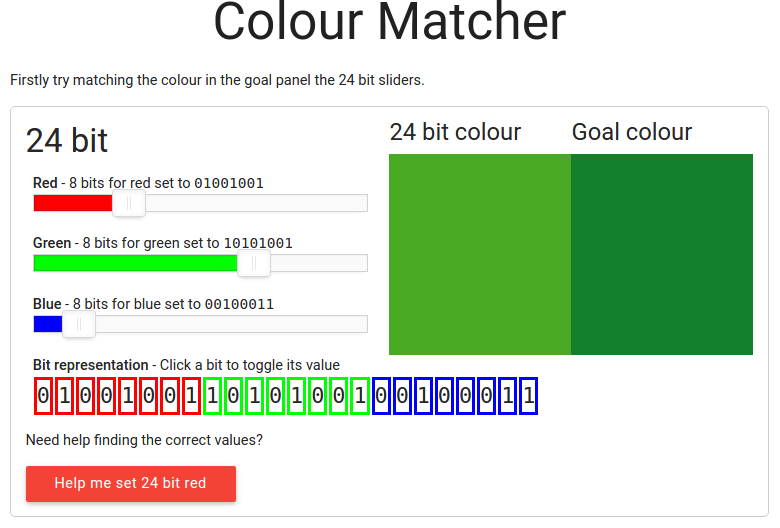
Wykonując eksperyment z użyciem poniższej aplikacji, można się przekonać, jaki będzie efekt zmniejszenia głębi koloru. Określ kolor klikając na obrazku po lewej stronie, a następnie spróbuj uzyskać odpowiednie dla wybranego koloru ustawienie suwaków 24-bitowych (po kilku próbach wyświetlony zostanie komunikat-wskazówka; zamiast myszy możesz używać strzałek na klawiaturze, aby precyzyjnie ustawić suwaki). Przekonasz się, że kolor można precyzyjnie opisać, używając reprezentacji 24-bitowej.
Następnie spróbuj to powtórzyć dla suwaków w wersji 8-bitowej. W tym przypadku na opis składowych czerwonej i zielonej przypadać będzie jedna z ośmiu możliwych wartości, a dla niebieskiej — jedna z czterech wartości.
W przypadku drugiego zestawu suwaków (w wersji 8-bitowej), na zapis informacji o składowej czerwowej przeznaczone były trzy bity. Na zapis składowej zielonej również trzy bity, a dla składowej niebieskiej tylko dwa. Oznacza to, że wzorzec bitowy koloru może być jednym z 256 możliwych.
Inaczej mówiąc: trzykrotne zmniejszenie liczby bitów z 24 do 8 ma taki skutek, że nie jesteśmy w stanie odziwerciedlić wielkiej liczby odcieni koloru, a więc i przedstawić łagodnego przejścia (gradientu) między ocieniami koloru na obrazie. To jest dobra ilustracja problemu, przed jakim stoi projektant oprogramowania: użyć mniej pamięci (mniejszej liczby bitów), czy uzyskać lepszą jakość zapisu (reprezentacji) informacji?
Dlaczego najmniejszą liczbę bitów przeznaczyliśmy na składową niebieską? Okazuje się, że ludzkie oko jest najmniej wrażliwe na kolor niebieski i dlatego tak można było postąpić. W komputerze łatwiej przetwarzać grupy składające się z 8 bitów niż z 9 bitów.
-
Co to jest?. Głębia koloru
Z informacją o liczbie bitów zastosowanych do zapisu informacji o kolorach pikseli wiąże się ściśle określenie „głębia koloru” (lub „głębia bitowa”). Przykład: obraz o 8-bitowej głębi koloru to taki, w którym każdy z pikseli ma przypisany jeden z 256 kolorów palety barw. Trzeba podkreślić, że drastyczne zmniejszenie głębi koloru może dać taki efekt, że obraz będzie wyglądał bardzo dziwnie (utrata kolorów prowadzi do powstania fałszywych konturów). Czasami taki efekt jest stosowany w programach graficznych specjalnie. Mówi się wtedy o efekcie posteryzacji (tj. upodobnieniu obrazu do plakatów, które drukuje się z użyciem tylko kilku kolorów).
-
Ciekawostka. Głębia koloru a kompresja
Jest subtelna różnica między zapisem informacji o obrazie z użyciem mniejszej liczby bitów (np. 8-bitowy kolor) a metodami kompresji. Choć redukacja liczby bitów do 8 skutkuje zmniejszeniem rozmiaru danych, to jednak takie podejście trudno nazwać skuteczną kompresją danych.
Kolejna aplikacja pozwala na pracę z dowolnym obrazem (np. z twojego komputera) i eksperymentowanie z przydzielaniem różnej liczby bitów do zapisu informacji o kolorze. Warto sprawdzić efekty na kilku przykładach, aby lepiej zrozumieć temat. Wybrany obraz z twojego dysku przeciągnij myszką w miejsce obrazu w tej chwili wyświetlanego.
Okazuje się, że głębia 8-bitowa, a nawet 16-bitowa, nie wystarcza do dobrego odzwierciedlenia subtelnych przejść tonalnych na skórze twarzy.
W innych przypadkach obrazy 16-bitowe mogą być prawie tak samo dobre, jak 24-bitowe.
Dzięki poniższej aplikacji możesz dostrzec efekt różnego przydziału bitów dla trzech składowych RGB.
-
Dla ciekawych. Czy kiedykolowiek potrzeba więcej niż 24 bity?
Można zapytać, czy zyskalibyśmy coś zapisując informację o kolorze z użyciem liczby bitów większej niż 24? Okazuje się, że ludzkie oko potrafi rozróżniać ok. 10 milionów kolorów, więc liczba kolorów dla głębi 24-bitowej (ponad 16 milionów) jest większa. Czasami jednak stosuje się więcej bitów, np. w przypadku, gdy chcemy na obrazie odzwierciedlić kontrast.
Rodzi się pytanie: Czy warto zaoszczędzić na pamięci, tracąc na jakości obrazu? W przypadku obrazu zapisanego z użyciem 24 bitów na piksel o rozmiarach 800 x 600 pikseli liczba bitów informacji o obrazie będzie równa 600 x 800 x 24 bity = 11 520 000 bitów, czyli ok. 1,44 megabajta. Jeśli zastosujemy 8 bitów na piksel, zaoszczędzimy 2/3 tej pamięci, czyli prawie 1MB.
Współcześnie rzadko używa się już systemu 8-bitowego. Jednak zdarza się, że stosuje się takie rozwiązanie np. w sytuacji zdalnej pracy na innym komputerze, z użyciem graficznego interfejsu użytkownika, kiedy nie ma szeropasmowego dostępu do sieci. Obraz pulpitu wygląda wtedy dziwnie, ale to nie ma wtedy większego znaczenia, bo ciągle jesteśmy w stanie wykonać pracę, którą zamierzaliśmy łącząc się z tym komputerem. Podobnie w przypadku tworzenia niektórych typów grafik, takich jak diagramy, czy rysunki czarno-białe (line art), stosuje się zmniejszoną liczbę bitów przy zapisie. Warto wspomnieć, że wiele ikon (pulpitu) jest 8-bitowych.
W sytuacji, kiedy chcemy uzyskać mniejszy rozmiar pliku z grafiką, bez znacznego pogarszania jakości obrazu, stosuje stosuje się powszechnie kompresję (np. JPEG, GIF i PNG). Taki zapis wymaga jednak pewnego czasu przetwarzania obrazu przy zapisie oraz odczycie, a więc wydłuża się czas potrzebny np. na wyświetlenie obrazu.
Więcej informacji znajdziesz w rozdziale poświęconym kompresji danych.
-
Uwaga
Lekturę tego podrozdziału warto poprzedzić zapoznaniem się opisem języków programowania niskiego poziomu w rozdziale Języki programowania.
W pamięci komputera zapisuje się binarnie również ciąg instrukcji tworzących program komputerowy.
Zwykle instrukcje składają się z dwóch części: kodu operacji i operandów.
li $t0, 10 #Umieść wartość 10 w rejestrze $t0
li $t1, 20 #Umieść wartość 20 w rejestrze $t1
#Dodaj wartości rejestrów $t0 i $t1, wynik dodawania umieść w rejestrze $a0
add $a0, $t0, $t1
W powyższym kodzie języka programowania niskiego poziomu skróty li i add oznaczają odpowiednio operacje „umieść wartość całkowitą” i „dodaj dwie wartości całkowite”. $t0, $t1 i $a0 są operandami (argumentami) i wskazują na miejsca (w rejestrach procesora), gdzie przechowuje się dane. 10 i 20 są argumentami dla instrukcji i oznaczają dosłownie liczby 10 i 20.
W przypadku 32-bitowego systemu operacyjnego każdą z powyższych instrukcji można by przedstawić jako cztery 8-bitowe fragmenty:
| operacja | Op1 | Op2 | Op3 |
|---|---|---|---|
| 00001000 | 00000000 | 00000000 | 00001010 |
| 00001000 | 00000001 | 00000000 | 00010100 |
| 00001010 | 10000000 | 00000000 | 00000001 |
Pierwsze 8 bitów 32-bitowej instrukcji określa jednoznacznie operację do wykonania. W powyższym przykładzie: 00001000 jest kodem operacji li a 00001010 jest kodem operacji add. Dla operacji li bity z kolumny Op1 określają miejsce, tj. 00000000 wskazuje na rejestr $t0. Podobnie dla operacji add bity z kolumny Op1 wskazują na rejestr $a0. Czy potrafisz odgadnąć, co oznaczają bity z kolumny Op3 dla każdej z instrukcji?
Dzięki temu, że za pomocą bitów w pamięci komputera przechowywane są zarówno instrukcje programu, jak i dane takie jak tekst, obrazy itp., również programy komputerowe mogą być zapisane na dysku w kodzie binarnym.
Informacje na temat binarnego zapisu grafiki zawarte w tym rozdziale to informacje podstawowe. Celem rozdziału było ukazać zasadę cyfrowego zapisu informacji oraz zwrócić uwagę na problem kompromisu między rozmiarem danych a jakością.
W podrozdziale dotyczącym kolorów poprzestano na opisie binarnego zapisu nieskompresowanych obrazów w postaci „surowej” czy bitmapy (format BMP). W praktyce dla obrazów dużych rozmiarów używa się metod kompresji takich, jak JPEG, GIF lub PNG. Należy podkreślić, że w momencie utworzenia obrazu (zdjęcia), czy wyświetlania na ekranie w sposób nieunikniony obraz ma reprezentację „surową”, o jakiej była mowa w tym rozdziale. Wybór docelowych parametrów zapisu obrazu i formatu pliku ma wpływ zarówno na jakość cyfrowej reprezentacji obrazu, jak i na koszt urządzenia, na którym docelowo obraz ma być wyświetlany.
Reprezentacja liczb jest obszernym tematem i jest przedmiotem badań naukowych. Wybór komputerowej reprezentacji ma ogromny wpływ np. na szybkość operacji arytmetycznych, dokładność wyniku oraz zapotrzebowanie na pamięć czy miejsce na dysku. Dla reprezentacji zmiennopozycyjnej liczb niecałkowitych określono standardy (najbardziej znany to IEEE 754), aby ułatwić projektowanie sprzętu komputerowego, który będzie zajmować się przetwarzaniem takich liczb. Arkusz kalkulacyjne zwykle używają reprezentacji zmiennopozycjnej do zapisywania wartości liczbowych, co ogranicza dokładność wykonywanych obliczeń (zwykle są używane 64 bity na każdą liczbę). Możesz sprawdzić, jakie są ograniczenia skończonej komputerowej reprezentacji liczb rzeczywistych np. wykonując dziele 1 przez 3 lub dodając w arkuszu kalkulacyjnym bardzo dużą liczbę do bardzo małej liczby.
Wiedza na temat ograniczeń komputerowej reprezentacji liczb jest istotna dla osoby zajmującej się programowaniem (np. w języku Python, Java, C, C++, C#), ponieważ programista musi dokonać wyboru typu danych. Jeśli źle wybierze, może nastąpić przepełnienie. Przykład: Jeśli programista zadeklaruje zmienną 16-bitową bez znaku, a następnie będzie w niej przechowywać informację o liczbie znaków w pliku tekstowym, to pojawi się błąd już w przypadku pliku o wielkości 65 kilobajtów.
Jeśli wielkość pamięci urządzenia komputerowego jest bardzo ograniczona (np. w małym przenośnym urządzeniu), programista nie będzie chciał rezerwować 32 bitów dla przechowywania informacji o liczbie, która nigdy nie przekroczy 100. Zresztą, nawet jeśli w urządzeniu rozmiar pamięci jest bardzo duży, to świadomy programista, wiedząc że program będzie przechowywał w pamięci miliony danych liczbowych, do zapisu których wystarczą reprezentacje 8-bitowe, nie będzie marnował milionów bajtów pamięci i używał reprezentacji 16-bitowych.
Nie zawsze jest to oczywiste, jakie rozmiary w pamięci komputera mają reprezentacje różnych typów danych w językach programowania (nie wynika to z nazwy typu). Zwykle deklaruje się je używając nazw typu „int” lub „long”, z których wprost nie wynika rozmiar rezerwowanej pamięci. Na przykład w języku Java są następujące typy całkowitoliczbowe: 8-bitowy typ byte, 16-bitowy typ short, 32-bitowy int i 64-bitowy long. W niektórych przypadkach (jak np. typ int w języku C) rozmiar rezerwowanej pamięci zależy od wersji języka i typu (architektury) komputera. W innych przypadkach (jak np. w języku Python) liczba bajtów niezbędna do zapisania liczby jest automatycznie zmieniana, jeśli liczba jest zbyt duża dla domyślnych ustawień.
W rozdziale pominęliśmy informacje na temat zapisu binarnego innego typu danych takich, jak np. pliki dźwiękowe i pliki wideo. Te zagadnienia będą dodane w uaktualnionej wersji przewodnika.
Warto zapoznać się z łamigłówkami na CS4FN (w języku angielskim), w których rozwiązaniu przydaje się znajomość zapisu binarnego.
Ta strona zawiera wiele informacji i ćwiczeń na temat arytmetyki komputerowej (w języku angielskim).
Poniższe materiały edukacyjne są w języku angielskim.
- CS Unplugged -- podstawy zapisu binarnego -- z polską instrukcją; samo ćwiczenie można też znaleźć jako scenariusz 1 w zbiorze scenariuszy po polsku.
- zapis bitów z użyciem dźwieku;
- gra Hex;
- artykuł Życie w naszym cyfrowym świecie;
- o zasadach działania dysku twardego.