-
Dla nauczyciela. Sztuczka parzystości w klasie
Magiczna sztuczka z użyciem tablicy parzystości może stanowić ciekawy wstęp do opowieści o korekcji błędów i zalecamy jej użycie na początku uczenia tego tematu. Trzeba ją wypróbować zawczasu. Dla uczniów szkół średnich zalecamy tablicę o wymiarach 7x7 lub 8x8, żeby wywarła odpowiednie wrażenie. Szczegóły znajdują się w scenariuszu 4 ,,Magia obracanych kart'' zbioru scenariuszy lekcji bez komputera.
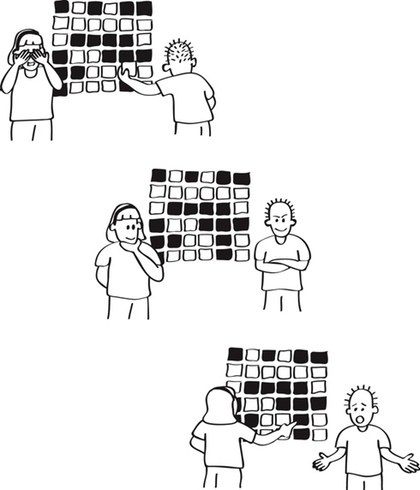
Magiczna sztuczka z parzystością (na powyższym filmie) umożliwia magikowi wykrycie, która z dziesiątek kart została odwrócona, gdy nie patrzył. Magia tej sztuczki to w rzeczywistości informatyka, wykorzystująca tę samą technikę, której używają komputery do wykrywania i korygowania błędów danych. Pokażemy, jak to działa, w następnym podrozdziale.
To samo dzieje się z danymi przechowywanymi na komputerach -- gdy ty (lub komputer) ich nie obserwujesz, niektóre z nich mogą się przypadkowo zmienić z powodu drobnej usterki. Nie chcielibyśmy, żeby komputer tak po prostu użył nieprawidłowych wartości, kiedy już je odczyta. Chcielibyśmy, żeby przynajmniej wykrył, że coś poszło nie tak, a najlepiej by było, gdyby zrobił to, co magik, czyli naprawił.
W tym rozdziale chodzi o ochronę przed błędami w danych w różnych postaciach -- w danych przechowywanych na dysku twardym, na dysku CD, dyskietce, dysku SSD (na przykład w telefonie komórkowym, aparacie lub odtwarzaczu mp3), danych znajdujących się w danej chwili w pamięci RAM (szczególnie na serwerach, w których poprawność danych jest niezwykle ważna), danych przepływających pomiędzy pamięcią RAM i dyskiem twardym lub między zewnętrznym dyskiem twardym a wewnętrznym dyskiem twardym, danych przetwarzanych właśnie w procesorze, czy danych przesyłanych przez sieci przewodowe lub bezprzewodowe, na przykład z twojego komputera na serwer po drugiej stronie świata. Obejmuje takie dane, jak kody kreskowe wydrukowane na produktach czy numery na kartach kredytowych.
Jeśli nie wykryjemy, że dane zostały zmienione przez jakiś problem fizyczny (na przykład małą rysę na płycie CD lub uszkodzony obwód w pamięci flash), niepoprawna informacja zostanie po prostu użyta. Bardzo źle napisany system bankowy może potencjalnie doprowadzić do zmiany salda twojego rachunku, gdyby tylko jeden z bitów w liczbie został zmieniony przez promień kosmiczny, wpływając na wartość w pamięci komputera! Jeśli kod paskowy na paczce czipsów zakupionej w sklepie zostanie zeskanowany nieprawidłowo, może zostać naliczona opłata za szampon. Jeśli prześlesz plik muzyczny z laptopa do odtwarzacza mp3, a kilka bitów zostało przesłanych nieprawidłowo, odtwarzacz mp3 może odtworzyć muzykę z irytującymi usterkami. Kody kontroli błędów chronią przed tym wszystkim, więc (zwykle) wszystko po prostu działa i nie musimy się obawiać takich błędów.
Dane mogą zostać przypadkowo zmienione z wielu powodów. Niektóre sieci mają dużo ,,szumu'' (spowodowanego złą jakością okablowania, zakłóceniami elektrycznymi lub -- w przypadku sieci bezprzewodowych -- zakłóceniami z innych sieci). Bity na dyskach są bardzo małe, a niedoskonałości na powierzchni mogą w końcu spowodować uszkodzenie pamięci. Powierzchnie na dyskach kompaktowych i DVD są odsłonięte i mogą być łatwo uszkodzone podczas przechowywania (na przykład w wysokiej temperaturze lub wilgotności) lub używania (na przykład przez zadrapania albo kurz). Błędy mogą również wystąpić przy wpisywaniu liczb, na przykład przy wprowadzaniu numeru konta bankowego w celu dokonania płatności lub numeru kontenera, który jest ładowany na statek. Kody kreskowe na produktach mogą być lekko zarysowane lub poplamione na czarno, albo opakowanie może być zgięte lub nie można go prawidłowo odczytać, ponieważ zbyt szybko przesunięto nad nim skaner. Zmiana bitów w pamięci trwałej (takiej jak dyski twarde, dyski optyczne i dyski półprzewodnikowe) jest czasami nazywana gniciem danych, a angielska strona Wikipedii o gniciu danych zawiera listę innych sposobów, w jakie mogą wystąpić te błędy.
Nikt nie chce komputera, który nie jest wiarygodny i nie robi tego, co powinien robić z powodu zmian bitów! Jak więc poradzić sobie z tymi problemami?
Kodowanie z korekcją błędów służy do wykrywania kiedy te błędy występują, a jeśli jest to możliwe i niezbyt kosztowne, poprawianie danych tak, aby wróciły do pierwotnej postaci.
Niektóre schematy kontroli błędów zawierają wbudowane kody korekcji błędów, takie jak metoda parzystości, o której wspomnieliśmy na początku tego rozdziału. Być może nie zrozumiałeś jeszcze, jak działała sztuczka z parzystością, ale po odwróceniu karty magik wykrył, która karta została przewrócona, i mógł ją poprawić.
Inne schematy kontroli błędów, takie jak te, które działają przy wysyłaniu danych z serwera za granicą do twojego komputera, wysyłają dane w bardzo małych fragmentach zwanych pakietami (mówi o tym rozdział o protokołach sieciowych) i każdy pakiet ma dodane informacje o wykryciu błędu.
Wykrywania błędów używa się również przy numerach kodów kreskowych na zakupionych produktach, numerach ISBN (International Standard Book Number), które mają wszystkie książki, a nawet 16-cyfrowych numerach na kartach kredytowych. Jeśli którykolwiek z tych numerów zostanie wpisany lub zeskanowany niepoprawnie, istnieje duża szansa, że błąd zostanie wykryty, a użytkownik może zostać poproszony o ponowne wprowadzenie danych.
Po przeczytaniu tego rozdziału powinieneś rozumieć: podstawową ideę kodowania kontroli błędów, powody, dla których tego wymagamy, różnice między algorytmami, które mogą wykrywać błędy, a tymi, które mogą zarówno wykrywać, jak i korygować błędy, a także znać niektóre z tych algorytmów, w szczególności parzystość (skupiając się na sztuczce parzystości) i cyfry kontrolne używane do zapewnienia prawidłowego wprowadzania numerów książek, numerów kodów kreskowych i numerów kart kredytowych.
Jeśli nigdy wcześniej nie widziałeś sztuczki z parzystością, obejrzyj wideo, które jest na początku rozdziału. Zakładamy w tym podrozdziale, że wiesz, co to znaczy sztuczka z parzystością, a teraz wyjaśnimy, jak ona działa!
Magik prosi obserwatora, aby ułożył dwustronne karty w kwadracie, a następnie magik mówi, że uczyni zadanie nieco trudniejszym, dodając do kwadratu dodatkową kolumnę i rząd. Magik odwraca się, a obserwator odwraca jedną z kart. Magik znowu się odwraca i mówi obserwatorowi, która karta została odwrócona!
Teraz pytanie brzmi: skąd magik wiedział, która karta została przewrócona, nie oglądając odwróconej karty, ani nie zapamiętując układu?! Krótko mówiąc, odpowiedzią jest korekcja błędów. Przyjrzyjmy się temu bliżej...
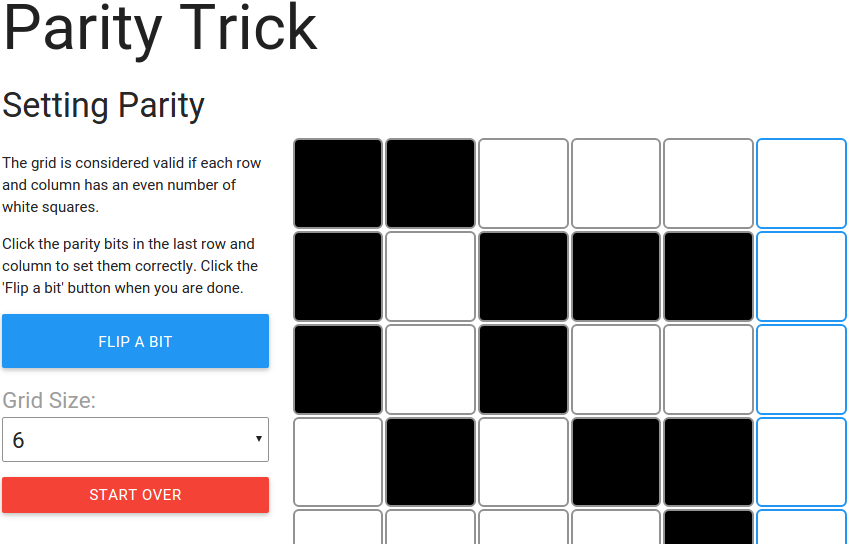
W poniższej aplikacji komputer ma kwadrat 7x7 z czarno-białych kart. Musisz wybrać kolor dodatkowej karty dla każdego rzędu (po prawej) i kolumny (na dole), tworząc kwadrat kart 8x8. Każda dodatkowa karta powinna zostać wybrana tak, aby każdy rząd i kolumna zawierały parzystą liczbę białych kart (ponieważ jest 8 kart w linii, liczba czarnych kart będzie również parzysta). Kartę w prawym dolnym rogu zawsze można wybrać tak, by jej wiersz i kolumna też miały parzystą liczbę białych pól.
Kiedy uznasz, że wszystko jest dobrze, powinieneś polecić komputerowi odwrócić kartę. Przez kilka sekund będzie pokazywana animacja, a następnie karty pojawią się ponownie, z jedną odwróconą kartą (cała reszta będzie taka sama jak poprzednio). Twoim zadaniem jest zidentyfikowanie odwróconej karty. Powinieneś to zrobić bez zapamiętania układu kart. Pamiętasz wzorzec, według którego dodawałeś dodatkowe karty? To on jest kluczem. Gdy uznasz, że zidentyfikowałeś kartę, kliknij ją, aby sprawdzić, czy masz rację. Aplikacja poprowadzi cię krok po kroku. Jeśli całkowicie utknąłeś podczas identyfikacji odwróconej karty, w aplikacji pojawi się podpowiedź, chociaż powinieneś najpierw spróbować ją znaleźć sam. Upewnij się, że dodajesz dodatkowe karty poprawnie; komputer nie powie ci, jeśli źle je ustawisz i prawdopodobnie nie będziesz w stanie zidentyfikować odwróconej karty, jeśli dodatkowe karty nie zostaną ustawione poprawnie.
Pamiętasz, jak ustawiałeś karty tak, aby każda kolumna miała parzystą liczbę białych kart? Kiedy karta zostaje odwrócona, powoduje to, że w wierszu i kolumnie znajduje się nieparzysta liczba białych kart. Wszystko, co musisz zrobić, to zidentyfikować rząd i kolumnę, które mają nieparzystą liczbę białych kart, a wtedy karta, która znajduje się na ich przecięciu, musi być tą, która została odwrócona!
To, co zobaczyliśmy powyżej, to prosty algorytm korekcji błędów, znany jako 2-wymiarowa kontrola parzystości.
Karty reprezentują bity, przy czym ich dwa stany to czerń i biel (w rozdziale o reprezentacji danych analizowaliśmy, jak bit może być przechowywany przez cokolwiek, co może być w jednym z dwóch stanów: błyszczący / matowy, namagnesowany / nienamagnesowany , wysokie napięcie / niskie napięcie, czerń / biel itp.). Karty w kracie 7x7, które komputer dla ciebie przygotował, mogą być jakimiś danymi, na przykład tekstem reprezentowanym za pomocą bitów, obrazem lub jakimiś liczbami. Chociaż są one rozmieszczone na kracie, na komputerze wiersze bitów będą przechowywane i przesyłane jeden po drugim (jako 8 partii po 8 bitów każda).
Dodatkowe, dodane przez ciebie karty są nazywane bitami parzystości. Parzystość oznacza po prostu, czy liczba jest parzysta czy nieparzysta (słowo pochodzi od tego samego rdzenia co ,,para''). Dodając dodatkowe karty w taki sposób, aby zapewnić parzystą liczbę białych kart w każdym rzędzie i kolumnie, sprawiłeś, że wiersze i kolumny miały tzw. własność parzystości.
Odwrócenie karty symulowało błąd w danych (np. kawałek kurzu lądujący na dysku CD lub promień kosmiczny zmieniający bit na dysku twardym, lub zakłócenia elektryczne zmieniające bit wysyłany przez kabel sieciowy). Ponieważ wiedziałeś, że w każdym wierszu i kolumnie powinna znajdować się parzysta liczba białych kart, byłeś w stanie stwierdzić, że wystąpił błąd, na podstawie faktu, że w kolumnie i wierszu była nieparzysta liczba białych kart. Oznacza to, że algorytm jest w stanie wykryć błędy, czyli była to detekcja błędów. Konkretna karta, która została odwrócona, znajdowała się na przecięciu wiersza i kolumny z nieparzystą liczbą białych kart, a ponieważ byłeś w stanie dokładnie określić, która karta została odwrócona, byłeś w stanie poprawić błąd. Tym samym to też algorytm korekcji błędów.
Gdybyś nie dodał bitów parzystości, nie byłbyś w stanie nawet stwierdzić, że wystąpił błąd, chyba że zapamiętałeś cały układ kart! A co by było, gdyby odwrócono więcej niż jedną kartę? Rozważymy to później.
-
Projekt. Bycie magikiem, czyli używanie sztuczki z parzystością jako sztuczki magicznej!
Teraz gdy już nauczyłeś się, jak działa sztuczka z parzystością, możesz wypróbować ją z fizycznym zestawem kart, jak magik w filmie, albo możesz użyć dowolnych obiektów z dwoma różnymi stronami, takimi jak monety lub kubki. Możesz używać kart do gry, ale oznaczenia mogą rozpraszać, a karty z dwoma kolorami są najłatwiejsze (możesz je wykonać, tnąc dwukolorowe arkusze tektury, albo jednokolorowy arkusz z naklejkami, albo zamalowany na jednej stronie).
Możesz znaleźć szczegóły i wiele pomysłów związanych ze sztuczką na stronie CS Unplugged (w języku angielskim) lub postępować zgodnie z tymi instrukcjami:
- Poproś przyjaciela, aby rozłożył 25 kart w siatce 5 na 5, starając się mieć w miarę losową mieszankę czarnych i białych (to mniej niż w aplikacji, ale łatwiej jest zaczynać z mniejszą liczbą kart, aby uniknąć błędów w następnym kroku!).
- Weź wszystkie pozostałe karty, a następnie powiedz, że w sumie 5 na 5 jest zbyt łatwe, więc zamierzasz przerobić je na 6 na 6. Zamiast dodawać losowo nowy wiersz i kolumnę, dodajesz je w taki sposób, w jaki robiłeś to w aplikacji (z parzystością). Zrób to tak szybko, jak tylko potrafisz, nie popełniając błędów (może to wyglądać bardzo naturalnie, jeśli to poćwiczysz, mimo że karty są starannie dobierane).
- Powiedz swojemu przyjacielowi, że się odwrócisz i chciałbyś, aby odwrócił jedną kartę, kiedy nie będziesz patrzył. Upewnij się, że odwrócił dokładnie jedną kartę.
- Odwróć się ponownie po odwróceniu karty, przejrzyj wiersze i kolumny, identyfikując wiersz, a następnie kolumnę zawierającą nieparzystą liczbę czarnych kart. Odwrócona karta będzie na przecięciu tego rzędu i kolumny. Odwróć tę kartę z powrotem.
Trzeba trochę ćwiczeń żeby móc dodać więcej kart i zidentyfikować odwróconą kartę tak, żeby obserwator nie zauważył, że się zastanawiasz. Przy odrobinie praktyki możesz to robić, swobodnie prowadząc rozmowę. Kiedy już dojdziesz do wprawy, będziesz mieć świetną sztuczkę na imprezy.
Aby uczynić ją bardziej efektowną, możesz udawać, że czytasz w myślach, machając rękami nad kartami. Szczególnie imponujące może być wprowadzenie asystenta do pokoju po odwróceniu karty; nawet jeśli nie widział wcześniej konfiguracji kart, i tak będzie w stanie wykryć błąd.
-
Dla nauczyciela. Ten podrozdział zawiera materiał rozszerzony
Ten podrozdział jest rozszerzeniem skierowanym do ciekawych uczniów. Dzieci w szkole podstawowej były w stanie zrozumieć wiele z tych pomysłów, choć tak naprawdę zależy to od zaangażowania uczniów w materiał.
W tym momencie powinieneś umieć wykonać sztuczkę z parzystością na tyle dobrze, że widać, że ją rozumiesz. Pozostała część tego rozdziału skupia się na dalszym badaniu pomysłów dotyczących korekcji błędów, związanych ze sztuczką z parzystością.
Najlepszym rozwiązaniem byłoby posiadanie fizycznych kart parzystości, które można rozmieścić przed sobą i przestawiać w trakcie rozważania postawionych pytań.
Algorytm korekcji błędów często łatwiej wykrywa błędy, niż je poprawia. Błędy na wielu bitach mogą czasami nawet pozostać zupełnie niewykryte. Co się stanie, jeśli komputer (lub twój przyjaciel, jeśli byłeś magikiem z prawdziwymi kartami parzystości), był sprytny i odwrócił dwie karty zamiast jednej? Możesz zacząć od namówienia przyjaciela lub kolegi z klasy, aby to zrobił. Powtórz to kilka razy. Czy zawsze potrafisz poprawić błędy, czy też czasem źle zgadujesz?
Pamiętaj, że aby wykryć błędy za pomocą tego algorytmu, wystarczy zauważyć że jeden lub więcej wierszy i / lub kolumn ma nieparzystą liczbę czerni i bieli -- wtedy musi istnieć co najmniej jeden błąd. Aby poprawić błędy, trzeba wskazać konkretne karty, które zostały odwrócone.
Czy zawsze jesteś w stanie wykryć, kiedy wystąpił błąd, jeśli zostały odwrócone 2 karty? Czemu? Czy zawsze jesteś w stanie poprawić błąd? A co gdyby były to 3 karty?
Okazuje się, że zawsze można wykryć błąd po odwróceniu 2 kart (tj. błąd 2-bitowy), ale system nie może naprawić błędu większego niż 1-bitowy. Kiedy dwie karty są odwrócone, będą co najmniej dwie opcje jak odwrócić dwie karty w celu przywrócenia parzystości, a ty nie będziesz wiedział, która z nich jest właściwa. Przy 3-bitowym błędzie (odwrócone 3 karty) zawsze będzie można wykryć błąd (nieparzystą liczbę białych bitów w co najmniej jednym rzędzie lub kolumnie), ale nie zawsze będzie można dokonać korekty. Przy odwracaniu 4 kart jest możliwe (choć niezbyt prawdopodobne), że błąd może pozostać niewykryty.
Rzeczywiście istnieje sposób na odwrócenie 4 kart tak, by błąd pozostał niewykryty, to znaczy żaden algorytm nie wykryje błędu inaczej niż przez przypadek. Czy potrafisz znaleźć znaleźć ten sposób?
Dzięki większej liczbie kart parzystości możemy wykryć i ewentualnie poprawić więcej błędów. Przyjrzyjmy się bardzo prostemu systemowi z minimalnymi liczbą kart parzystości. Możemy mieć tablicę 7x7 z danymi i tylko jedną kartę parzystości. Ta karta parzystości sprawia, że w całym układzie znajduje się parzysta liczba białych kart (w tym karta parzystości). Jak można tego użyć do wykrywania błędów? Czy jesteś w stanie kiedykolwiek poprawić błędy w tym systemie? W jakich sytuacjach błędy pozostają niezauważone? Rozważ sytuacje z różną liczbą błedów (tzn. odwróconych kart).
Przy użyciu tylko jednej dodatkowej karty do sprawdzania parzystości można wykryć błąd pojedynczego bitu (całkowita liczba czarnych kart stanie się nieparzysta), ale 2-bitowy błąd nie zostanie wykryty, ponieważ liczba białych kart będzie ponownie parzysta. Zostanie wykryty 3-bitowy błąd, ale ogólnie rzecz biorąc, ten system jest dość zawodny.
Wracając do powyższej sztuczki z parzystością, w której była tablica 7x7 i 15 kart parzystości rozszerzających tablicę do wymiaru 8x8, warto zauważyć, że potrzebna była tylko jedna dodatkowa karta do wykrycia, że wystąpił błąd, ale aż 15 dodatkowych do poprawienia błędu. Można powiedzieć, że w algorytmie znacznie więcej miejsca kosztuje poprawianie błędów, niż po prostu ich wykrywanie!
Co się dzieje, gdy używamy tablicy o innych rozmiarach? Wiersz czy kolumna nie musi mieć parzystej liczby białych kart i parzystej liczby czarnych kart, po prostu tak akurat jest w przypadku tablicy o parzystym boku (np. o najczęściej w tym podrozdziale używanym rozmiarze 8x8).
Rozszerz tablicę 6x6 za pomocą kart parzystości do tablicy 7x7. Karty parzystości muszą sprawić, że każdy rząd i kolumna ma parzystą liczbę białych kart (w tym przypadku zawsze będzie nieparzysta liczba czarnych kart w każdym rzędzie i kolumnie). Wykrywanie błędów polega na szukaniu wierszy i kolumn zawierających nieparzystą liczbę białych kart (ale parzysta liczbę czarnych). Co ciekawe, tablica nie musi nawet być kwadratowa! Możesz użyć 4x7 i też będzie działać!
Nie ma również ograniczeń rozmiaru. Możesz utworzyć tablicę 10x10 (100 kart) i nadal możesz wykryć, która karta została przewrócona. Większe tablice czynią magiczną sztuczkę jeszcze bardziej imponującą.
Prawdopodobnie nie byłbyś zadowolony, gdybyś kupił książkę przez Internet, wpisując numer ISBN (International Standard Book Number), i wysłano by Ci niewłaściwą książkę, lub jeśli kilka dni po jej zamówieniu otrzymałbyś email z informacją, że podany numer karty kredytowej nie należał do Ciebie, tylko miał jedną zmienioną cyfrę, a inny posiadacz karty kredytowej poskarżył się na bezprawne obciążenie jego karty. Albo gdybyś poszedł do sklepu kupić puszkę napoju, a skaner odczytał ją jako droższy produkt. Czasami skaner nawet nie odczytuje kodu kreskowego, a operator kasy ręcznie musi wprowadzić numer do komputera -- ale jeśli nie wprowadzi go dokładnie tak, jak widnieje na kodzie kreskowym, może się okazać, że zostanie naliczona opłata za niewłaściwy produkt. Wszystko to są przykłady sytuacji, którym korekcja błędów może zapobiec.
Numery kodów kreskowych, numery kart kredytowych, numery kont bankowych, numery ISBN, numery PESEL, etykiety wysyłkowe (kody kontenerów wysyłkowych -- SSCC) i numery podatkowe zawierają kody korekcji błędów, aby zmniejszyć ryzyko ich wystąpienia. Niektóre cyfry w takich numerach to cyfry kontrolne, które uzyskuje się, wykonując specjalne obliczenia na wszystkich pozostałych cyfrach w numerze. Jeśli na przykład wpiszesz numer karty kredytowej w formularzu internetowym, aby coś kupić, zostanie obliczone, jaka powinna być 16. cyfra, przy użyciu pierwszych 15 cyfr i specjalnego sposobu (w numerach kart kredytowych jest 16 cyfr). Jeśli oczekiwana 16. cyfra nie jest cyfrą, którą wprowadziłeś, można stwierdzić, że wystąpił błąd przy wprowadzeniu numeru i zostaniesz powiadomiony, że numer karty kredytowej jest nieprawidłowy.
W następnym podrozdziale najpierw przyjrzymy się jednemu z najczęściej używanych formatów kodów kreskowych, używanych w większości produktów kupowanych w sklepach. Później rozpatrzymy numery kart kredytowych. Nie musisz rozumieć dlaczego obliczenia działają tak dobrze (jest to zaawansowana matematyka i nie jest to ważne dla zrozumienia ogólnej idei) i chociaż dobrze jest wiedzieć, jakie są obliczenia, nie jest to niezbędne. Więc jeśli matematyka jest dla ciebie wyzwaniem i cię niepokoi, nie panikuj za bardzo, ponieważ to, co oglądamy w tym podrozdziale, nie jest wcale tak trudne, jak mogłoby się początkowo wydawać!
Większość produktów, które można kupić w sklepie, ma kod kreskowy z 13-cyfrowym ,,globalnym numerem handlowym'' (zwanym GTIN-13). Pierwsze 12 cyfr to rzeczywisty numer identyfikacyjny produktu, 13. to cyfra kontrolna wyliczana z pozostałych 12. Nie wszystkie kody kreskowe to GTIN-13, istnieje kilka innych typów. Jeśli jednak kod kreskowy zawiera 13 liczb, to prawie na pewno jest to GTIN-13.
Ostatnia cyfra tych liczb jest wyliczana z pierwszych 12. Jest to bardzo ściśle związane z bitem parzystości, który rozważaliśmy powyżej, gdzie ostatni bit rzędu jest ,,wyliczany'' z wcześniejszych bitów. Kod GTIN-13 pozwala nam wykryć, czy jedna z cyfr nie została wprowadzona niepoprawnie.
Następująca aplikacja sprawdza kody kreskowe GTIN-13. Wprowadź pierwsze 12 cyfr kodu kreskowego, a aplikacja powie ci, jaka powinna być ostatnia cyfra! Możesz zacząć używając numeru kodu kreskowego 9 300675 036009.
-
Dla nauczyciela. Pozyskiwanie większej ilości kodów kreskowych
Możesz przynieść różne opakowania, które mają kody kreskowe, żeby klasa mogła je ocenić, albo przynieść zdjęcia kodów kreskowych.
Co się stanie, jeśli popełnisz błąd podczas wpisywania 12 cyfr (spróbuj zmienić jedną cyfrę)? Czy można wykryć, że popełniono błąd?
-
Dla nauczyciela. Rozwiązanie
Jeśli zmieni się tylko jedna cyfra, cyfra kontrolna będzie zawsze nieprawidłowa, a błąd zostanie wykryty.
Znajdź inny produkt z kodem kreskowym, np. artykuł spożywczy lub przedmiot papierniczy. Zauważ, że niektóre kody kreskowe są trochę inne -- upewnij się, że kody kreskowe, których używasz, mają 13 cyfr (chociaż możesz też dowiedzieć się, jak działa cyfra kontrolna na innych kodach). Czy aplikacja zawsze jest w stanie określić, czy poprawnie wpisałeś kod kreskowy?
Jeden z następujących numerów produktów zawiera jedną niepoprawną cyfrę. Czy możesz stwierdzić, przy pomocy aplikacji, który z produktów miał nieprawidłowo wpisany numer?
- 9 400550 619775
- 9 400559 001014
- 9 300617 013199
-
Dla nauczyciela. Rozwiązanie
Ostatni kod zawiera literówkę; powinno być 9 300617 003199. Uczniowie powinni być w stanie wykryć, że jest nieprawidłowy, ale nie da się ustalić, jaka jest właściwa wartość.
Gdybyś skanował powyższe kody kreskowe w sklepie, niepoprawny musiałby zostać ponownie przeskanowany, a system może stwierdzić, że jest to zła liczba, bez konieczności wyszukiwania w spisie. Zwykle błędy są spowodowane uszkodzeniem samego kodu kreskowego (np. trochę lodu na zamrożonym produkcie, powodujące nieprawidłowy odczyt). Jeśli zostanie wykryty błąd, skaner zwykle wydaje dźwięk ostrzegawczy, aby ostrzec kasjera.
Możesz spróbować wymienić się numerami kodów kreskowych z kolegami z klasy, ale przed podaniem numeru rzuć monetą i jeśli wyjdzie orzeł, zmień jedną z cyfr kodu kreskowego, zanim go podasz. Czy uda im się ustalić, że dostali błędny kod kreskowy?
Jeśli jedna cyfra jest niepoprawna, to wyliczona cyfra kontrolna da inną wartość niż ma cyfra w kodzie, co zasygnalizuje błąd. Tak więc błędy jednocyfrowe zawsze zostaną wykryte, ale co jeśli dwie cyfry ulegną zmianie -- czy zawsze błąd zostanie wykryty?
-
Dla nauczyciela. Rozwiązanie
Jeśli zostaną zmienione dwie cyfry, błąd może pozostać niewykryty; na przykład zmiana 9 400559 001014 na 6 500559 001014 nadal będzie generować sumę kontrolną 4, która wydaje się być zgodna. Jednak jest mało prawdopodobne, że dwa błędy tak się zniosą (uczniowie mogą zbadać, jak często to się dzieje).
Co jeśli błąd występuje w samej sumie kontrolnej, ale nie w innych cyfrach -- czy zostanie wykryty?
-
Dla nauczyciela. Rozwiązanie
Niektórzy uczniowie mogą się martwić, że wystąpi problem, jeśli to suma kontrolna zostanie zmieniona, ale oczywiście jeśli zostanie ona wpisana niepoprawnie, to nie będzie ona pasować do sumy innych cyfr, a błąd zostanie wykryty.
Ludzie mogą popełniać błędy, przy wprowadzaniu liczb do komputerów i nawet skanery kodów kreskowych mogą błędnie odczytać jakąś cyfrę. Cyfry kontrolne starają się wykryć, że wystąpił błąd i powiadamiają o tym komputer i / lub osobę. Załóżmy, że podajesz numer telefonu komórkowego znajomemu, aby mógł się z tobą później skontaktować. Aby upewnić się, że prawidłowo podałeś numer, możesz poprosić go o natychmiastowe wysłanie SMSa, żeby to potwierdzić (i żebyś też zaraz miał jego numer). Jeśli nie dostaniesz tego SMSa, prawdopodobnie ponownie sprawdzisz numer i odkryjesz, że twój znajomy popełnił błąd, na przykład źle wpisał cyfrę lub odwrócił dwie cyfry leżące obok siebie. Błędy się zdarzają, a dobre systemy zapobiegają irytującym lub nawet poważnym konsekwencjom tych błędów. Jeśli używana jest cyfra kontrolna, istnieje duża szansa, że błąd zostanie wykryty, gdy cyfra kontrolna nie jest zgodna z oczekiwaniami komputera.
Niektóre z ludzkich, typowych błędów to:
- nieprawidłowa jedna cyfra (podstawienie),
- zamiana miejscami dwóch sąsiadujących cyfr (transpozycja),
- brakująca cyfra,
- dodana cyfra.
Dwa ostatnie zostaną zauważone przez niezgodność z oczekiwaną długością liczby; na przykład GTIN-13 ma 13 cyfr, więc jeśli wprowadzono 12 lub 14, komputer natychmiast wie, że coś jest nie w porządku. Wykrycie pierwszych dwóch polega na cyfrze kontrolnej. Co ciekawe, wszystkie jednocyfrowe błędy zostaną wykryte przez popularne systemy sum kontrolnych, a większość transpozycji też zostanie wykryta (czy możesz znaleźć przykłady transpozycji, które nie zostały wykryte, korzystając z powyższej aplikacji?).
Istnieją również mniej powszechne błędy, popełniane przez ludzi:
- nieprawidłowa cyfra w dwóch lub więcej miejscach,
- podwojenie błędnej cyfry, np. umieszczenie 3481120 zamiast 3481220,
- pomieszanie 3 cyfr, np. 14829 zamiast 12489,
- błędy fonetyczne są możliwe, gdy numer został odczytany i wpisany przez kogoś słuchającego (lub czytającego sobie głośno ten numer podczas wpisywania); na przykład ,,trzydzieści'' (30) może być usłyszane jako ,,trzynaście'' (13).
Eksperymentuj dalej. Jakie błędy zostały wykryte? Jakie znajdziesz błędy, które nie zostaną wykryte? Czy typowe błędy prawie zawsze zostają wykryte? Czy potrafisz znaleźć sytuacje, w których nie zostają? Spróbuj znaleźć przykłady tylu różnych rodzajów wykrywalnych i niewykrywalnych błędów, ile tylko możesz.
-
Dla nauczyciela. Częste błędy
Uczniowie mogą próbować odwrócić wszystkie cyfry lub całkowicie je zmienić i pokazać, że cyfra kontrolna pozostaje taka sama, a następnie twierdzić, że jest to ograniczenie algorytmu, ale nie jest to dobra ocena. Muszą myśleć o tym, jak algorytm jest normalnie używany, np. przez kasjera wprowadzającego numer kodu kreskowego do komputera, pielęgniarkę wprowadzającą numer identyfikacyjny pacjenta lub kogoś, kto kupuje coś online i podaje numer karty kredytowej, czyli rozważyć błędy, których realistycznie można się spodziewać. Błędy wymienione powyżej dobrze obejmują możliwe rodzaje błędów, chociaż uczniowie mogą wymyślić więcej. Oczywiście ważniejsze jest, żeby wykrywać błędy naprawdę powszechne, ale miło byłoby, gdyby wykrywane były też mniej popularne, choć nadal mogące wystąpić. Należy jednak pamiętać, że dla algorytmu byłoby większym problemem, gdyby nie mógł wykryć zmiany 1 cyfry, niż gdyby na przykład nie można było wykryć zmiany 3 cyfr.
Główne błędy, które ten system najlepiej wykryje, to jednocyfrowe literówki i zamiana dwóch sąsiednich cyfr. Dla innych rodzajów błędów to bardziej kwestia przypadku.
Dysleksja i związane z nią problemy mogą być interesującą kwestią do rozważenia, chociaż należy zachować odpowiednie proporcje, ponieważ większość ludzi nie ma dysleksji.
-
Dla nauczyciela. Pisanie programu wykrywania błędów
Skłonienie uczniów do napisania programu do obliczania sum kontrolnych jest dobrym ćwiczeniem programistycznym. Można zadanie uprościć poprzez założenie, że użytkownik będzie wpisywał każdą cyfrę osobno, lub można rozdzielenie cyfr we wpisanym ciągu uczynić częścią ćwiczenia. Utworzenie arkusza kalkulacyjnego do tych obliczeń również nie jest trudne.
Pierwsze 12 cyfr kodu kreskowego przedstawia informacje takie jak kraj pochodzenia, producent i identyfikator produktu. 13. cyfra to cyfra kontrolna, wyliczana z pierwszych 12 cyfr. Jest obliczana przy użyciu następującego algorytmu (zobacz także przykład poniżej).
- Pomnóż co drugą cyfrę (począwszy od drugiej) przez 3, a resztę przez 1 (czyli pozostają bez zmian).
- Dodaj wszystkie pomnożone liczby, otrzymując sumę.
- Cyfra kontrolna to ta liczba, którą należałoby dodać do sumy żeby uczynić ją wielokrotnością 10 (tj. ostatnia cyfra sumy powinna wynosić 0). Albo, bardziej formalnie, weź ostatnią cyfrę sumy i jeśli jest 0, to cyfra kontrolna wynosi 0. W przeciwnym razie odejmij ostatnią cyfrę od 10, aby uzyskać cyfrę kontrolną.
Spójrzmy na przykład ilustrujący ten algorytm. Chcemy potwierdzić, że cyfra kontrolna umieszczona na kodzie kreskowym butelki soku była poprawna. Numer kodu kreskowego to 9300675032247. Ostatnia cyfra, 7, to cyfra kontrolna. Bierzemy więc pierwsze 12 cyfr i mnożymy je przez 1 lub 3, w zależności od ich pozycji (9x1+3x3+0x1+0x3+6x1+7x3+5x1+0x3+3x1+2x3+2x1+4x3). Następnie sumujemy wszystkie pomnożone liczby, otrzymując sumę 73. Chcemy dodać taką cyfrę kontrolną, która doprowadzi sumę do najbliższej wielokrotności 10, która wynosi 80. Ta liczba to 7, która jest rzeczywiście cyfrą kontrolną na kodzie kreskowym butelki soku.
Poniższa aplikacja może być używana do wykonywania za ciebie obliczeń. Aby upewnić się, że rozumiesz proces, sam musisz wykonać niektóre czynności; aplikacji możesz użyć do szerokiej gamy systemów z cyfrą kontrolną. Aby sprawdzić numer GTIN-13, wprowadź pierwsze 12 cyfr w miejsce przy którym jest napisane ,,Enter the number here''. Mnożniki dla GTIN-13 można wprowadzić jako 131313131313 (co druga cyfra pomnożona przez 3). To da iloczyny każdej z 12 cyfr pomnożonych przez odpowiednią liczbę. Powinieneś samodzielnie obliczyć sumę iloczynów (liczb w okienkach) i ją wpisać. Następnie otrzymasz resztę z dzielenia przez 10. Aby obliczyć cyfrę kontrolną, należy obliczyć cyfrę potrzebną do dopełnienia tej liczby do 10 (na przykład, jeśli reszta to 8, cyfra kontrolna to 2). Jeśli reszta to 0, to cyfra kontrolna również wynosi 0.
Spróbuj z innymi kodami kreskowymi. Teraz popatrz, co dzieje się w obliczeniach, gdy zmieni się cyfrę, lub dwie cyfry zamieni się miejscami.
Algorytm sprawdzania, czy numer kodu kreskowego został poprawnie wprowadzony, jest bardzo podobny. Można obliczyć cyfrę kontrolną i porównać ją z 13. cyfrą, ale prościej jest liczyć na wszystkich 13 cyfrach.
Pomnóż co drugą cyfrę (począwszy od drugiej) przez 3, a pozostałe przez 1. Łącznie z 13. cyfrą, która jest mnożona przez 1. Dodaj wszystkie pomnożone liczby, aby otrzymać sumę. Jeśli ostatnia cyfra sumy wynosi 0, numer został wprowadzony poprawnie. (To oznacza, że reszta z dzielenia przez 10 wynosi 0).
-
Ciekawostka. Wyliczanie sumy kontrolnej w pamięci
W przypadku 13-cyfrowych kodów kreskowych szybkim sposobem otrzymania sumy kontrolnej, dającym się wyliczyć w pamięci (przy pewnej wprawie), jest wzięcie osobno liczb, które mają być pomnożone przez 3, dodanie ich, a następnie pomnożenie przez 3. Dla przykładu powyżej (9300675032247) dwie grupy liczb to 9+0+6+5+3+2+7=32 i 3+0+7+0+2+4=16. Więc dodajemy 32 + 16x3, co daje sumę 80 łącznie z cyfrą kontrolną.
Aby było jeszcze łatwiej, przy każdym dodawaniu wystarczy pamiętać ostatnią cyfrę, ponieważ pozostałe cyfry nigdy nie wpłyną na końcowy wynik. Na przykład pierwsze dodawanie powyżej zaczyna się od 9+0+6, więc możesz powiedzieć, że daje to 5 (zamiast 15). Następna cyfra (5) zmienia sumę na 0 i tak dalej. Oznacza to również, że możesz grupować cyfry, które razem dają 10 (jak 1 i 9 lub 5 i 5) i je zignorować. Na przykład w drugiej grupie 3+0+7 na początku sumuje się do 0, a jedyną sumą, która się będzie liczyć, jest 2+4, co daje w wyniku 6.
Nawet mnożenie będzie w porządku, jeśli po prostu weźmiesz ostatnią cyfrę. W powyższym przykładzie oznacza to, że kończymy wyliczając 6x3, co daje 8 (nie 18); w nieuproszczonym mnożeniu było 16x3, co daje 48, ale jedyną liczącą się cyfrą będzie ostatnie 8.
Wszystkie te skróty mogą bardzo ułatwić liczenie sumy w pamięci.
-
Dla nauczyciela. Sprawdzanie a obliczanie
Uczniowie powinni być w stanie dostrzec związek między tymi dwoma algorytmami (wyznaczaniem cyfry kontrolnej w porównaniu z dodawaniem wszystkich 13 cyfr żeby je sprawdzić). Ponieważ 13. cyfra znajduje się na pozycji o nieparzystym numerze, zostaje pomnożona przez 1 w drugim algorytmie, zanim zostanie dodana do sumy. Ponieważ cyfra kontrolna została wybrana tak, aby ostatnia cyfra sumowała się do wielokrotności 10 (która zawsze kończy się na 0), to jeśli liczba w drugim algorytmie została poprawnie wprowadzona, suma też będzie kończyła się na 0.
-
Dla ekspertów. Dlaczego ten algorytm działa tak dobrze?
Aby być skutecznym, algorytm musi zapewnić, że pomnożone cyfry nie zsumują się do wielokrotności 10, gdyby zostały tylko nieznacznie zmienione. Wybór mnożników wpływa na prawdopodobieństwo wykrycia niewielkich zmian w danych wejściowych. Możliwe jest matematyczne przeanalizowanie tego, jakie rodzaje błędów da się wykryć.
Zasadniczo co druga cyfra jest mnożona przez 3, a suma tych wielokrotności jest dodawana do pozostałych cyfr. Spójrzmy na kilka mniejszych przykładów z 5 cyframi (4 cyfry normalne i cyfra kontrolna), ponieważ te same pomysły będą miały zastosowanie do 13 cyfr.
Jeśli potrzebujemy cyfry kontrolnej dla 8954, obliczalibyśmy (8x1)+(9x3)+(5x1)+(4x3)=52, a aby zwiększyć tę wartość do 60, musimy dodać 8. Czyli pełnym numerem będzie 89548.
Pierwszą rzeczą, którą powinniśmy zauważyć jest to, że tylko cyfra jedności (ostatnia cyfra) każdej dodanej liczby ma wpływ na cyfrę kontrolną. 8+27+5+12=52 i 8+7+5+2=22 (patrzymy tylko na ostatnią cyfrę każdej dodawanej liczby). Obie liczby kończą się na 2, a zatem potrzebują 8, aby utworzyły najbliższą wielokrotność 10. Możesz dostrzec, dlaczego tak jest, jeśli zauważysz, że ,,2'' i ,,1'', które zostały wycięte z kolumny dziesiątek, dają 10+20=30, co jest wielokrotnością 10. Odejmowanie ich wpływa tylko na kolumnę dziesiątek i wyżej. Tak jest zawsze i dlatego możemy uprościć problem, dodając do sumy tylko cyfrę jedności każdej liczby. (Może to również służyć jako skrót do obliczania sumy kontrolnej w pamięci).
Ochrona przed pojedynczymi błędami
Przyjrzyjmy się teraz, dlaczego zmiana jednej cyfry w liczbie na inną cyfrę zawsze zostanie wykryta za pomocą tego algorytmu. Każda cyfra będzie dodawać liczbę od 0 do 9 do sumy (pamiętajmy, że teraz zależy nam tylko na kolumnie jedności). Skoro zmiana cyfry spowoduje, że doda ona inną liczbę do sumy, niemożliwe będzie żeby suma ciągle dawała wielokrotność 10. Pamiętaj, że każda cyfra jest pomnożona przez 1 lub 3, zanim jej kolumna jedności zostaje dodana do sumy.
Liczba pomnożona przez 1 zawsze będzie w całości dodana do sumy. Jeżeli na przykład którąś taką cyfrą była 9, to żadna inna cyfra nie może dodać 9 do sumy. Więc cyfry pomnożone przez 1 są w porządku.
Ale co z liczbami pomnożonymi przez 3? Aby odpowiedzieć na to pytanie, musimy spojrzeć na to, jaki wkład każda inna cyfra wnosi do sumy kiedy się ją pomnoży przez 3.
- 1 -> 3
- 2 -> 6
- 3 -> 9
- 4 -> 2 (od 12)
- 5 -> 5 (od 15)
- 6 -> 8 (od 18)
- 7 -> 1 (od 21)
- 8 -> 4 (od 24)
- 9 -> 7 (od 27)
- 0 -> 0
Patrząc na kolumnę po prawej stronie, widać, że żadna liczba się nie powtarza. Oznacza to, że nie ma takich cyfr, które wnosiłyby do sumy tę samą wartość, gdy się je pomnoży przez 3.
Stąd właśnie wiemy, że wszystkie jednocyfrowe błędy zostaną wykryte.
Zabezpieczenie przed zamianą sąsiednich cyfr
Znacznie trudniej dostrzec dlaczego algorytm chroni przed większością błędów zamiany cyfr.
Jeśli dwie cyfry są obok siebie, jedna z nich musi być pomnożona przez 1, a druga przez 3. Jeśli są zamienione -- to na odwrót. Na przykład, jeśli poprzednio wymieniony numer 89548 zostanie zmieniony na 85948, wówczas do sumy dodaje się (5x3)+(9x1)=24 zamiast (9x3)+(5x1)=32. Ponieważ cyfry jedności 24 i 32 są inne, liczba dodana do sumy jest inna, a zatem błąd zostanie wykryty.
Ale czy są przypadki, w których cyfry jedności sum będą takie same? Innym sposobem spojrzenia na problem jest pobranie pary wierszy z powyższej listy, na przykład:
- 8 -> 4
- 2 -> 6
Pamiętaj, że pierwsza kolumna określa, ile wniosą do sumy cyfry pomnożone przez 1, a druga kolumna -- cyfry pomnożone przez 3. Ponieważ sąsiednie cyfry są pomnożone przez inną wartość (jedna przez 3, a druga przez 1), zostaną dodane liczby leżące po przekątnej w wybranej parze.
Jeśli na przykład pierwsze 2 cyfry w liczbie to ,,28'', dodamy 2+4=6 do sumy. Jeśli zostaną zamienione miejscami, dodamy 8+6=14, co odpowiada 4, ponieważ wielokrotności ,,10'' nie mają wpływu na sumę. 8+6 i 2+4 leżą na przekątnej pary!
- 8 -> 4
- 2 -> 6
Zatem pytanie brzmi: czy widzisz jakieś pary, w których suma przekątnych dawałaby tę samą wartość? Jest taka para!
Ochrona przed błędami podwojenia
Błąd podwojenia polega na tym, że cyfra, która powtarza się dwukrotnie w liczbie, zmienia się na inną cyfrę, która powtarza się dwukrotnie. Na przykład, jeśli mamy liczbę ,,22'' w numerze, ktoś może jakoś ją zmienić na ,,88''.
Gdy dwie liczby są obok siebie, jedna jest pomnożona przez 3, a druga przez 1. Wartość wniesiona do sumy jest sumą wiersza danej liczby na powyższej liście. Na przykład 2 ma wiersz ,,2->6''. Oznacza to, że 2+6=8 zostanie dodane do sumy z powodu tych dwóch cyfr.
Jeśli jakieś wiersze sumują się do tej samej liczby, może to stanowić problem. Gdy suma przekracza 10, kolumna dziesiątek została usunięta.
- 1 -> 3 sumuje się do ,,4''
- 2 -> 6 sumuje się do ,,8''
- 3 -> 9 sumuje się do ,,2''
- 4 -> 2 sumuje się do ,,6''
- 5 -> 5 sumuje się do ,,0''
- 6 -> 8 sumuje się do ,,4''
- 7 -> 1 sumuje się do ,,8''
- 8 -> 4 sumuje się do ,,2''
- 9 -> 7 sumuje się do ,,6''
- 0 -> 0 sumuje się do ,,0''
Niektóre wiersze sumują się do tej samej liczby! Ponieważ zarówno czwarty, jak i dziewiąty wiersz dają sumę 6, błąd nie zostanie wykryty, jeśli w badanym numerze ,,44'' zostanie zamienione na ,,99''!
Błędy dotyczące wierszy, które nie sumują się do tej samej liczby, zostaną wykryte. Z powyższego przykładu wynika, że jeśli 22 zmieni się na 88, zostanie to wykryte, ponieważ 22 sumuje się do 8, a 88 sumuje się do 2.
Błąd, który nigdy nie zostanie wykryty
Innym błędem, czasem przez ludzi popełnianym, jest błąd transpozycji ze skokiem. Polega on na tym, że zostają zamienione dwie cyfry, które mają jedną cyfrę między nimi, na przykład 812 zamienia się w 218.
Para cyfr, które są od siebie oddzielone jedną cyfrą, będzie zawsze mnożona przez te same wartości -- 1 lub 3. Oznacza to, że zmiana pozycji liczb nie wpływa na to, przez co są pomnożone, a więc nie wpływa na sumę. Tak więc tego rodzaju błąd nigdy nie zostanie wykryty.
-
Projekt. Projekt z sumą kontrolną
Poniższa aplikacja wygeneruje losowe numery wybranego typu (np. numery ISBN dla książek). Te numery są losowe i nie są oparte na numerach rzeczywistych książek (ani kont bankowych!). Oznacza to, że możesz wykonać ten projekt bez konieczności proszenia kogokolwiek o podanie swoich danych osobowych, takich jak numery kart kredytowych (w rzeczywistości nie powinni podawać ci tych informacji!).
Chociaż numery z tej aplikacji są losowe, ich cyfry kontrolne są obliczane przy użyciu odpowiedniej metody, więc możesz użyć ich jako przykładów w twoim projekcie. Program czasem celowo popełnia błąd i nie zawsze cyfra kontrolna będzie poprawna, więc jednym z twoich zadań jest ustalenie, które są w porządku!
Generator liczb
Niektóre z poniższych kodów są poprawne, a niektóre nie.
Kody są generowane bez kresek, spacji itp.
Twój projekt polega na wybraniu innych numerów niż 13-cyfrowe kody kreskowe i sprawdzeniu, w jaki sposób jest obliczana suma kontrolna (wszystkie używają nieco różnych mnożników). Powinieneś pokazać, jak działa obliczanie sumy kontrolnej (używając aplikacji, jeśli chcesz) i odkryć, które z wygenerowanych numerów są nieprawidłowe.
ISBN-10 jest szczególnie skuteczny i możesz spróbować sprawdzić, dlaczego tak jest.
Kody omówione w tym rozdziale są szeroko stosowane, ale kody najczęściej używane do przechowywania danych są bardziej wyrafinowane, ponieważ muszą radzić sobie z bardziej złożonymi błędami niż zmiana pojedynczego bitu. Na przykład, jeśli płyta CD jest porysowana, albo dysk twardy ma małe uszkodzenie, prawdopodobnie wpłynie to na wiele sąsiednich bitów. Systemy te wykorzystują kody oparte na bardziej zaawansowanej matematyce. Najczęściej używanymi kodami do przechowywania i przesyłania danych są kody Reeda-Solomona i cykliczny kod nadmiarowy (CRC). W przypadku numerów czytelnych dla człowieka, takich jak kody kreskowe, numery bankowe, numery podatkowe, numery PESEL itd., najpowszechniejsze są sumy kontrolne, a algorytm Luhna jest jednym z najczęściej używanych. Większe sumy kontrolne są również używane do sprawdzania, czy pliki zostały pobrane poprawnie. Metoda parzystości jest rodzajem kodu Hamminga.
Wszystkie poniższe materiały są w języku angielskim.
- materiały multimedialne na temat sztuczki z parzystością na stronie CS Unplugged;
- CS4FN udostępnia darmową książkę ze sztuczką z parzystością i kilkoma innymi sztuczkami związanymi z informatyką.
- Techradar zawiera sporo informacji na temat wykrywania i korekcji błędów.
- o kodach korekcji błędów;
- kalkulator wyliczający cyfry kontrolne w popularnych kodach kreskowych.