8. Kodowanie -- szyfrowanie

Szyfrowanie służy do zachowania poufności danych. Najprościej rzecz ujmując, plik lub przesyłane dane są zniekształcane tak, że tylko właściwe osoby posiadające tajny ,,klucz'' mogą odtworzyć oryginalny tekst. Gdy korzystasz z urządzeń cyfrowych, cały czas używasz systemów opartych na szyfrowaniu: kiedy korzystasz z bankowości internetowej, łączysz się z siecią Wi-Fi, płacisz kartą płatniczą (wkładając ją do czytnika, przesuwając pasek magnetyczny, albo dotykając czytnika); naprawdę wokół prawie każdej czynności pojawi się szyfrowanie. Bez szyfrowania twoje informacje byłyby dostępne dla całego świata - każdy mógłby podjechać pod Twój dom i odczytać wszystkie dane przechodzące przez Twoją sieć Wi-Fi, a skradzione laptopy, dyski twarde i karty SIM byłyby źródłem wielu informacji o Tobie - więc szyfrowanie ma kluczowe znaczenie dla użyteczności systemów komputerowych.

System szyfrowania często składa się z dwóch programów komputerowych: pierwszy służy do zaszyfrowania danych (nazywanych tekstem jawnym), przekształcając je w coś przypominającego bzdury (szyfrogram), a drugi program służy do odszyfrowania szyfrogramu, zmieniając go z powrotem w tekst jawny. Szyfrowanie i deszyfrowanie polegają na użyciu bardzo sprytnych operacji matematycznych na tekście za pomocą wybranego klucza. Wkrótce dowiesz się więcej o tych pojęciach.

Oczywiście nie potrzebowalibyśmy szyfrowania, gdybyśmy żyli w świecie, w którym wszyscy byliby uczciwi i moglibyśmy im ufać -- wtedy każdy mógłby mieć dostęp do wszystkich Twoich danych osobowych, na przykład dokumentacji medycznej, wszystkiego co pisałeś w sieci, kont bankowych itd. i wiedzielibyśmy, że nikt by nie ingerował w takie rzeczy jak systemy kontroli samolotów i broń sterowana komputerowo. Jednak informacje są cenne, ludzie cenią sobie prywatność, a bezpieczeństwo jest ważne, dlatego szyfrowanie jest podstawą przy projektowaniu systemów komputerowych. Nawet złamanie zabezpieczeń systemu sygnalizacji świetlnej może być wykorzystane dla osiągnięcia osobistej korzyści.

Dużym problemem związanym z systemami szyfrowania są ludzie, którzy chcą się do nich włamać i odszyfrować wiadomości bez klucza (który jest jakąś tajną wartością, która może być użyta do odblokowania zaszyfrowanego pliku). Niektóre systemy, używane wiele lat temu, okazały się być niewystarczająco zabezpieczone przed takimi atakami, więc nie można ich już używać. Możliwe, że ktoś kiedyś znajdzie skuteczny sposób włamywania się do systemów powszechnie używanych obecnie, co spowodowałoby wiele problemów.

Jak każdą technologię, szyfrowanie można wykorzystać do dobrych i złych celów. Organizacja broniąca praw człowieka może użyć szyfrowania, aby potajemnie wysłać zdjęcia nadużyć w zakresie praw człowieka do mediów, a handlarze narkotyków mogą go użyć, aby zabezpieczyć swoje plany przed śledczymi. Zrozumienie w jaki sposób szyfrowanie działa i co jest możliwe przy jego użyciu, może pomóc w podejmowaniu świadomych decyzji dotyczących takich rzeczy jak wolność słowa, prawa człowieka, śledzenie działalności przestępczej, prywatność, kradzież tożsamości, bankowość i płatności internetowe oraz bezpieczeństwo systemów, które mogą zostać przejęte, jeśli zostały ,,zhakowane''.

Przyjrzymy się teraz prostemu szyfrowi podstawieniowemu nazywanemu szyfrem Cezara. Szyfr Cezara ma ponad 2000 lat i został wynaleziony przez Juliusza Cezara. Zanim przejdziemy dalej, spróbuj złamać ten prosty kod. Jeśli utkniesz, spróbuj popracować w małej grupie z przyjaciółmi i kolegami z klasy, aby móc wspólnie omawiać pomysły. Do wykonania tego ćwiczenia przyda się tablica lub długopis i papier.

TEDBY YN ZYVENXSK NY ZYVXYMI 
MJOUKT XK WSCTO BKDEXUYGK. 
EJITOWI ROVSUYZDOBK, MSOJKBYGOU S MJYVQYG.
LKNJ QYDYGI NY EMSOMJUS QNI DIVUY 
BYJVOQXK CSO DBJI QVYCXO CIQXKVI QGSJNUK. 
LONO WSKV MJOBGYXK YZKCUO XK BOMO.

Gdy już zorientujesz się, co mówi tekst, ułóż tabelę z literami alfabetu w kolejności, a następnie wpisz literę, którą każda z nich reprezentuje w szyfrogramie. Powinieneś zauważyć ciekawy wzór.

Biorąc pod uwagę, jak łatwo można złamać ten szyfr, prawdopodobnie nie chciałbyś, aby Twoje dane bankowe były nim zaszyfrowane. W praktyce używa się znacznie silniejszych szyfrów, choć na razie będziemy dalej analizować szyfrowanie szyfrem Cezara, ponieważ jest to znakomite wprowadzenie do wielu pojęć związanych z szyfrowaniem.

Kiedy poznałeś szyfr Cezara w poprzednim podrozdziale i (miejmy nadzieję) złamałeś go, i odkryłeś, co mówi wiadomość, prawdopodobnie zauważyłeś jakie było powiązanie liter pierwotnej wiadomości z literami w odszyfrowanej wiadomości. Każda litera w pierwotnej wiadomości została zdekodowana do litery, która znajdowała się 10 miejsc przed nią w alfabecie. Sporządzona tabela powinna to pokazać. Oto tabela powiązań liter, w której litera K jest przyporządkowana literze A. Jeśli Twoja tabela jest odwrotna, czyli pokazuje zmianę A na K zamiast K na A, to też wszystko w porządku. Jeśli nie byłeś w stanie złamać szyfru Cezara w poprzednim podrozdziale, wróć do niego teraz i zdekoduj przy użyciu tabeli.

W tym przykładzie mówimy, że kluczem jest 10, ponieważ klucze w szyfrze Cezara są liczbami od 1 do 25 (zastanów się, dlaczego nie chcemy liczby 26 jako klucza), które określają, jak daleko należy przesunąć alfabet. Gdybyśmy zamiast tego użyli klucza 8, tabela konwersji będzie następująca.

Spróbuj eksperymentować z następującą aplikacją dla szyfru Cezara. Być może przyda ci się też później, podczas ćwiczeń w dalszych podrozdziałach dotyczących szyfru Cezara.

Wcześniej przyjrzeliśmy się łamaniu szyfru Cezara -- otrzymywaniu tekstu jawnego z zaszyfrowanego tekstu bez posiadania klucza. Jest jeszcze łatwiej odszyfrować szyfr Cezara, gdy mamy klucz. W praktyce dobry system szyfrowania zapewnia, że ​​tekst jawny nie może być uzyskany z zaszyfrowanego tekstu bez klucza, tj. może być odszyfrowany, ale nie złamany.

Jako przykład deszyfrowania za pomocą szyfru Cezara, załóżmy, że mamy następujący zaszyfrowany tekst i że klucz to 6.

GRG SG QUZG O JAFKMU VYG

Ponieważ wiemy, że klucz to 6, możemy odjąć 6 miejsc od każdej litery w zaszyfrowanym tekście. Na przykład litera o sześć miejsc przed G to A, 6 miejsc przed R to L, a 6 miejsc przed S to M. Z tego wiemy, że pierwsze słowa to ALA MA. Przechodząc przez cały tekst zaszyfrowany, uzyskamy w ten sposób tekst jawny:

ALA MA KOTA I DUZEGO PSA

Powyższa aplikacja może wykonać ten proces za Ciebie. Wystarczy umieścić tekst zaszyfrowany w polu po prawej stronie, wpisać klucz i nakazać odszyfrowanie. Powinieneś jednak wiedzieć jak samemu szyfrować wiadomości!

Szyfrowanie jest równie proste. Zamiast obracać się do tyłu (odejmowanie), tak jak zrobiliśmy przy odszyfrowywaniu, obracamy do przodu (dodajemy) każdą literę w tekście o tyle miejsc, ile wynosi klucz. Załóżmy na przykład, że chcemy zaszyfrować poniższy tekst kluczem 7.

JAK SIE MASZ

Zaczęlibyśmy od ustalenia, że literą o 7 miejsc za J jest Q, 7 miejsc za A znajduje się H, a 7 miejsc za K mamy R. Oznacza to, że pierwsze słowo tekstu jawnego zaszyfrujemy do QHR w zaszyfrowanym tekście. Przechodząc przez cały tekst jawny, uzyskamy w ten sposób tekst zaszyfrowany:

QHR ZPL THZG

Do tej pory rozważaliśmy jeden sposób złamania szyfru Cezara: używanie wzorców w tekście. Poszukując charakterystycznych wzorców, takich jak jednoliterowe słowa, inne krótkie słowa, podwójne litery i znając reguły, takie jak to, że wszystkie słowa muszą zawierać co najmniej jedną samogłoskę (z wyjątkiem niektórych skrótów czy słów pisanych ,,po SMSowemu''), łatwo złamać szyfr Cezara. Żadnego dobrego kryptosystemu nie powinno dać się analizować w ten sposób, tzn. system powinien być semantycznie bezpieczny.

Istnieje wiele innych sposobów na złamanie szyfru Cezara, którym przyjrzymy się w tej sekcji. Zrozumienie różnych prostych ataków na szyfry będzie ważne, gdy będziemy patrzeć na wyszukane, używane w praktyce kryptosystemy.

Analiza częstotliwościowa polega na sprawdzaniu, ile razy każda litera pojawia się w zaszyfrowanej wiadomości, i wykorzystaniu tej informacji do złamania kodu. Jeśli litera pojawia się wiele razy w wiadomości, to jest o wiele bardziej prawdopodobne, że jest to A niż na przykład F.

Poniższa aplikacja ułatwia analizę fragmentu tekstu poprzez zliczanie częstotliwości liter. Możesz wkleić tekst, aby zobaczyć, które litery występują najczęściej i najrzadziej.

Następujący tekst został zakodowany przy użyciu szyfru Cezara. Aby spróbować go zrozumieć, wklej go do analizatora statystycznego powyżej.

IQZLF BNFITRTXH EFBNJWF BNJQJ 
XYFYDXYDHESDHM BXPFETBJP PYTWDHM 
RTESF ZEDH IT FSFQNED PYTWJ QNYJWD 
BDXYJUZOF SFOHEJXHNJO, F B 
QFRFSNZ XEDKWZ RTLF SFBJY UTRTH 
SFOHEJXYXEJ UFWD QZG YWTOPN QNYJW

A jest najczęstszą literą alfabetu polskiego. Rozsądne byłoby więc przypuszczenie, że F w zaszyfrowanym tekście odpowiada A w tekście jawnym. Ponieważ F jest o 5 liter po literze A w alfabecie, możemy się domyślić, że kluczem jest 5. Jeśli umieścisz tekst zaszyfrowany w poniższej aplikacji i ustawisz klucz o wartości 5, przekonasz się, że jest to rzeczywiście poprawny klucz. Możesz dla jasności obrazu powiększyc okienko tekstowe za pomocą prawego, dolnego trójkącika w okienku.

Jak głosi komunikat, długie wiadomości zawierają wiele wskazówek statystycznych. Bardzo krótkie wiadomości (np. tylko kilka słów) prawdopodobnie nie będą miały oczywistych trendów statystycznych. W bardzo długich wiadomościach (np. w całych książkach) prawie zawsze litera A występuje najczęściej. Wikipedia ma listę częstotliwości liter, które mogą ci się przydać.

Innym rodzajem ataku jest atak ze znanym tekstem jawnym, w którym znasz część lub całe rozwiązanie. Na przykład, jeśli wiesz, że wszystkie moje wiadomości zaczynam od DZIEN DOBRY, możesz łatwo znaleźć klucz dla następującej wiadomości.

WSBXG WHUKR MTCGX LIHMDTGBX HWUXWSBX LBX P LHUHMX H ZHWSBGBX WKNZBXC

Nawet jeśli nie wiesz, że kluczem jest proste przesunięcie (nie wszystkie szyfry podstawieniowe takie są), to wiesz że D->W, Z->S, I->B, E->X, N->G, O->H, B->U, R->K, Y->R. To znacznie ułatwia rozszyfrowanie wiadomości. Wypisując znane litery, otrzymasz:

WSBXG WHUKR MTCGX LIHMDTGBX HWUXWSBX LBX P LHUHMX H ZHWSBGBX WKNZBXC
DZIEN DOBRY ___NE __O___NIE ODBEDZIE _IE _ _OBO_E O _ODZINIE DR__IE_

Znając wyżej podane sztuczki, wiemy że istnieje bardzo ograniczona liczba możliwości dla pozostałych liter. Spróbuj odszyfrować powyższy tekst.

Atak ze znanym tekstem jawnym od razu łamie szyfr Cezara, ale dobry kryptosystem nie powinien mieć takiej luki, ponieważ ktoś może zaskakująco łatwo domyślić się, że dana wiadomość została wysłana. Na przykład typową wiadomością może być ,,nic do zgłoszenia''. W bankowości internetowej najprawdopodobniej pojawią się typowe komunikaty, takie jak nagłówki na rachunku bankowym lub części strony internetowej, które zawsze są wyświetlane. Jeszcze gorszy jest atak z wybranym tekstem jawnym, w którym ktoś skłania użytkownika, żeby wysłał wybraną wiadomość za pośrednictwem swojego systemu, żeby atakujący mógł zobaczyć, jaki jest odpowiadający jej szyfrogram.

Z tego powodu istotne jest, aby dobry kryptosystem nie był możliwy do złamania, nawet jeśli atakujący posiada fragmenty tekstu jawnego wraz z odpowiadającym im szyfrogramem. W tym celu kryptosystem powinien dawać inny zaszyfrowany tekst za każdym razem, gdy zaszyfrowana jest ta sama wiadomość. Początkowo może wydawać się to niemożliwe, chociaż istnieje kilka sprytnych technik stosowanych w prawdziwych systemach kryptograficznych.

Innym podejściem do łamania szyfrogramu jest atak brutalny, który polega na wypróbowaniu wszystkich możliwych kluczy i sprawdzeniu, czy któryś z nich nie tworzy zrozumiałego tekstu. Jest to łatwe dla szyfru Cezara, ponieważ istnieje tylko 25 możliwych kluczy. Na przykład poniższy szyfrogram to pojedyncze słowo, ale jest zbyt krótkie, by przeprowadzić statystyczny atak. Umieść go w powyższym dekoderze i próbuj różne klucze, aż odszyfrujesz.

EIJUDJQSOZDYU

W obecnie stosowanych szyfrach, klucze szyfrowania są zwykle liczbami o długości 128 bitów lub więcej. Można obliczyć, ile czasu zajęłoby wypróbowanie wszystkich możliwych 128-bitowych liczb, jeśli komputer mógłby przetestować milion na sekundę (w tym testując, czy każdy zdekodowany tekst zawiera polskie słowa). W końcu to odkryje wiadomość, ale po upływie czasu, którego to będzie wymagało, będzie mało prawdopodobne, aby jeszcze się to do czegokolwiek przydało -- a użytkownik klucza prawdopodobnie go zmienił!

Jeśli to policzymy, testowanie 128-bitowy klucza w tempie 1 000 000 na sekundę zajmie 10 790 283 070 000 000 000 000 000 lat. Oczywiście można znaleźć coś już w pierwszym roku, ale szanse na to są absurdalnie niskie i bardziej realistyczne byłoby mieć nadzieję na zdobycie najwyższej nagrody w Lotto trzy razy z rzędu (a prawdopodobnie zapewniłoby to więcej pieniędzy). Średnio będzie to zajmować około połowę tego czasu, czyli nieco ponad 5 000 000 000 000 000 000 000 000 lat. Nawet jeśli masz naprawdę szybki komputer, który może sprawdzić jeden bilion kluczy na sekundę (w praktyce jest to mało realne), zajmie to około 5 000 000 000 000 000 lat. Nawet gdybyś mógł zdobyć milion takich komputerów (jeszcze mniej realne w praktyce), to wymagałoby to 5 000 000 lat.

A nawet gdybyś miał sprzęt, który rozważaliśmy powyżej, ludzie zaczęliby używać większych kluczy. Każdy bit dodany do klucza podwoi liczbę lat potrzebnych do jego odgadnięcia. Wystarczy dodać 15 lub 20 bitów więcej do klucza w powyższym przykładzie, aby zwiększyć wymagany czas do wartości znacznie dłużej niż oczekiwany czas życia Ziemi i Słońca! W ten sposób prawdziwe kryptosystemy chronią się przed atakami brutalnymi. Kryptografia w wielu przypadkach opiera się na niskich prawdopodobieństwach sukcesu.

Poniższy kalkulator potrafi dokonywać obliczeń na naprawdę wielkich liczbach. Jeśli chcesz, możesz sprawdzić nasze powyższe obliczenia! Sprawdź również, co by się stało, gdyby rozmiar klucza był podwójny (tj. 256 bitów) lub gdyby został użyty klucz 1024 lub 2048 bitowy (co jest w dzisiejszych czasach powszechne).

Opisane powyżej systemy podstawieniowe nie zapewniają żadnego zabezpieczenia w nowoczesnych systemach komputerowych. W dalszej części tego rozdziału przyjrzymy się systemom szyfrowania, które są używane w praktyce. Pierwszym wyzwaniem jest znalezienie sposobu na wymianę kluczy -- jeśli komunikujesz się z kimś przez Internet, jak zamierzasz wysłać mu klucz do swojej tajnej wiadomości?

Kryptosystemy są również wykorzystywane do celów takich jak uwierzytelnianie (sprawdzanie hasła). Wydaje się to łatwe, ale jak sprawdzić, czy ktoś się loguje, bez konieczności przechowywania hasła (w końcu, jeśli ktoś uzyskał listę haseł, może to zrujnować twoją reputację i firmę, więc bezpieczniej jest ich w ogóle nie przechowywać.)

Istnieją dobre rozwiązania tych problemów, które są powszechnie używane -- w rzeczywistości prawdopodobnie używasz ich już online, być może nawet o tym nie wiedząc! Zaczniemy od spojrzenia na systemy, które umożliwiają odkodowywanie tajnych wiadomości bez konieczności wysyłania klucza.

Jeśli Alicja wysyła zaszyfrowaną wiadomość do Boba, powoduje to interesujący problem w szyfrowaniu. Sam szyfrogram może być bezpiecznie wysłany przez ,,niebezpieczną'' sieć (podsłuchiwaną przez Ewę), ale klucz -- nie. Jak Alicja może dostarczyć klucz Bobowi? Pamiętaj, że klucz to jest to, co mówi Bobowi, jak przekształcić szyfrogram z powrotem w tekst jawny. Zatem Alicja nie może umieścić go w zaszyfrowanej wiadomości, ponieważ wtedy Bob nie mógłby uzyskać do niego dostępu. Alicja nie może po prostu włączyć go do wiadomości jako zwykły tekst, ponieważ wtedy Ewa będzie mogła go pobrać i użyć go do odszyfrowania wiadomości, które będą nim zaszyfrowane. Możesz zapytać, dlaczego Alicja nie zaszyfruje klucza za pomocą innego schematu szyfrowania, ale skąd Bob miałby znać ten nowy klucz? Alicja musiałaby przekazać Bobowi klucz, który został użyty do jego zaszyfrowania... i tak dalej... Ten pomysł nie zadziała!

Pamiętaj, że Alicja i Bob mogą być w różnych krajach i mogą komunikować się tylko przez Internet. To również wyklucza przekazanie klucza Bobowi osobiście przez Alicję.

Fizyczna dystrybucja kluczy jest bardzo kosztowna, a do lat 70. XX wieku wydawano duże sumy na fizyczne wysyłanie kluczy za granicę. Takie systemy są nazywane szyfrowaniem symetrycznym, ponieważ Alicja i Bob potrzebują identycznej kopii klucza. Przełomem było odkrycie, że można stworzyć system wykorzystujący różne klucze do kodowania i dekodowania. Przyjrzymy się temu bliżej w następnym podrozdziale.

Jednym z niezwykłych odkryć w dziedzinie informatyki w latach 70. była metoda zwana szyfrowaniem z kluczem publicznym, w której można powiedzieć wszystkim, co jest kluczem do szyfrowania wiadomości, ale do odszyfrowania potrzebny jest specjalny klucz prywatny. Ponieważ Alicja i Bob używają różnych kluczy, nazywa się to asymetrycznym systemem szyfrowania.

To tak, jakby rozdawać kłódki wszystkim swoim znajomym, aby każdy mógł zamknąć pudełko i wysłać je do ciebie, ale jeśli masz jedyny (prywatny) klucz, to jesteś jedyną osobą, która może otworzyć pudełka. Gdy znajomy zamknie pudełko, nawet on nie będzie mógł go otworzyć. Dystrybucja kłódek jest bardzo łatwa. Klucze publiczne są takie same -- możesz je upublicznić -- często ludzie umieszczają je na swojej stronie internetowej lub dołączają do wszystkich emaili, które wysyłają. To zupełnie inna jakość niż konieczność wynajęcia firmy ochroniarskiej, która dostarczy je twoim kolegom.

Szyfrowanie z kluczem publicznym jest bardzo często wykorzystywane w handlu elektronicznym (takim jak bankowość internetowa i płatność kartą kredytową), ponieważ komputer może nawiązać połączenie z firmą lub bankiem automatycznie, korzystając z publicznego klucza, bez konieczności wcześniejszego spotkania w celu uzgodnienia klucza. Systemy klucza publicznego są zwykle wolniejsze od systemów symetrycznych, dlatego system kluczy publicznych jest często używany do wysyłania nowego klucza dla systemu symetrycznego tylko raz na sesję, a od tego momentu klucz symetryczny może już być używany do szybszego, symetrycznego systemu szyfrowania.

Bardzo popularnym systemem klucza publicznego jest RSA. W tym podrozdziale dotyczącym systemów z kluczem publicznym użyjemy RSA jako przykładu.

Po pierwsze, musisz wygenerować parę kluczy za pomocą interaktywnego generatora kluczy. Powinieneś zachować klucz prywatny w tajemnicy i publicznie ogłaszać klucz publiczny, aby twoi znajomi mogli wysyłać ci wiadomości (np. umieść je na tablicy lub wyślij je pocztą elektroniczną do znajomych). Upewnij się, że masz gdzieś zapisane klucze, żeby ich nie zapomnieć -- najlepiej w pliku tekstowym.

Poniższa aplikacja jest szyfratorem i służy do szyfrowania wiadomości za pomocą klucza publicznego. Twoi przyjaciele powinni użyć go do zaszyfrowania wiadomości.

Aby się upewnić, że rozumiesz, spróbuj zaszyfrować krótką wiadomość za pomocą klucza publicznego. W następnym podrozdziale znajduje się narzędzie do odszyfrowania wiadomości za pomocą klucza prywatnego.

Poniższa aplikacja jest deszyfratorem. Służy do odszyfrowywania wiadomości zaszyfrowanych za pomocą klucza publicznego. Aby odszyfrować wiadomości, potrzebujesz klucza prywatnego.

Nawet gdy twoi wrogowie znają twój klucz publiczny (skoro go publicznie ogłosiłeś), nie mogą go użyć do odszyfrowania wiadomości, które zostały zaszyfrowane przy jego użyciu. Jesteś jedyną osobą, która może odszyfrować wiadomości, ponieważ wymaga to klucza prywatnego, do którego, miejmy nadzieję, tylko ty masz dostęp.

Zauważ, że implementacja RSA w tej aplikacji jest po prostu demonstracją koncepcji i nie jest zupełnie taka sama jak implementacje używane w systemach szyfrowania wykorzystywanych w rzeczywistości.

Naprawdę interesującym zagadnieniem w szyfrowaniu jest przechowywanie haseł w taki sposób, że nawet jeśli baza danych z hasłami zostanie ujawniona, hasła nie będą miały użytecznej postaci. Taki system ma wiele pozornie sprzecznych wymagań.

• Kiedy użytkownik się loguje, musi być możliwe sprawdzenie, czy wprowadzono poprawne hasło.
• Nawet jeśli baza danych wycieknie, a atakujący ma ogromną moc obliczeniową...
• Baza danych nie powinna zdradzać oczywistych informacji, takich jak długości haseł, użytkowników, którzy wybierali te same hasła, częstotliwości liter w hasłach lub wzorców w hasłach.
• Użytkownicy powinni mieć co najmniej kilka dni / tygodni, aby móc zmienić hasło, zanim napastnik je złamie. Najlepiej byłoby, gdyby nigdy nie uzyskał hasła.
• Nie powinno być możliwości odzyskania zapomnianego hasła. Jeśli użytkownik zapomni hasła, musi ono zostać zmienione. Nawet administratorzy systemu nie powinni mieć dostępu do hasła użytkownika.

Większość systemów logowania ma limit, ile razy można zgadywać hasło. Chroni to wszystkie hasła, oprócz najgorzej wybranych, przed odgadnięciem przez dobrze zaprojektowany formularz logowania. Wykrywanie podejrzanego logowania przez sprawdzanie adresu IP i kraju pochodzenia również staje się coraz częstsze. Jednak żadne z tych wymuszonych zabezpieczeń nie działa, gdy atakujący ma kopię bazy danych i może użyć tyle mocy obliczeniowej, ile chce, bez ograniczeń nakładanych przez aplikację. Jest to często nazywane atakiem offline, ponieważ atakujący może zaatakować bazę danych u siebie.

W tym podrozdziale przyjrzymy się kilku szeroko stosowanym algorytmom bezpiecznego przechowywania haseł. Następnie przyjrzymy się kilku przypadkom, w których wyciekły duże bazy danych. Bezpieczne przechowywanie haseł sprowadza się do używania sprytnych algorytmów i technik szyfrowania oraz sprawienia, by użytkownicy wybierali skuteczne hasła. Wiedza na temat przechowywania haseł może również pomóc w zrozumieniu znaczenia wyboru dobrych haseł i nieużywania tego samego hasła w wielu różnych, ważnych stronach WWW.

Algorytm haszowania to algorytm, który przyjmuje hasło i wykonuje na nim złożone obliczenia, a następnie zwraca pozornie losowy ciąg znaków zwany skrótem lub haszem. Ten proces nazywa się haszowaniem. Dobre algorytmy haszowania mają następujące właściwości:

• Za każdym razem, gdy dane hasło jest haszowane, powinno ono dawać ten sam skrót.
• Mając dany konkretny hasz, nie powinno być możliwe szybkie wyliczenie oryginalnego hasła.

Matematycznie algorytm skrótu nazywany jest funkcją jednokierunkową. Oznacza to po prostu, że bardzo łatwo jest obliczyć hasz danego hasła, ale próba odzyskania hasła z danego hasza może być wykonana tylko przez atak brutalny. Innymi słowy, łatwo jest robić w jedną stronę, ale prawie niemożliwe jest odwrócenie. Popularny algorytm haszowania nazywa się SHA-256. Pozostała część tego rozdziału skupi się na SHA-256.

Jest to świetne rozwiązanie problemu haseł. Zamiast przechowywać hasła w naszej bazie danych, możemy przechowywać skróty. Gdy użytkownik zarejestruje się lub zmieni swoje hasło, musimy po prostu przetworzyć hasło za pomocą algorytmu SHA-256, a następnie zapisać wynikowy skrót zamiast hasła. Gdy użytkownik chce się zalogować, musimy ponownie wprowadzić hasło do algorytmu SHA-256. Jeśli wyjściowy skrót jest zgodny z przechowywanym w bazie danych, to użytkownik musiał wprowadzić poprawne hasło. Jeśli atakujący zdoła uzyskać dostęp do bazy danych z hasłami, nie będzie w stanie ustalić rzeczywistych haseł. Same skróty nie są atakującemu przydatne.

Poniższa aplikacja umożliwia haszowanie słów, takich jak hasła (ale nie należy umieszczać w nich prawdziwego hasła, ponieważ nigdy nie należy wpisywać hasła w losowych witrynach). Jeśli wprowadzisz dobrze dobrane hasło (np. losowy ciąg cyfr i liter) i będzie ono miało wystarczającą długość, będziesz mógł bez obaw umieścić skrót na publicznej stronie internetowej, a nikt nie będzie w stanie określić, jakie było twoje hasło.

Na przykład poniższa tabela bazy danych pokazuje czterech użytkowników fikcyjnego systemu i skróty ich haseł. Możesz wyznaczyć ich hasła, wprowadzając różne możliwości do algorytmu SHA-256 i sprawdzając, czy dane wyjściowe są takie same jak któreś hasło w bazie danych.

To może początkowo brzmieć tak, jakbyśmy mieli doskonały system. Ale niestety nadal istnieje duży problem. Możesz znaleźć w sieci tęczowe tablice, które są zawczasu przeliczonymi listami popularnych haseł z wartościami, do których się haszują. Nie jest trudno wygenerować tęczowe tabele zawierające wszystkie hasła do określonej wielkości (jest to jeden z powodów, dla których zdecydowanie zaleca się używanie długich haseł!). Tego problemu można uniknąć, wybierając hasło, które nie jest często spotykanym słowem lub kombinacją słów.

Haszowanie to dobry początek, ale musimy jeszcze ulepszyć nasz system, żeby dwaj użytkownicy wybierający to samo hasło mieli różne hasze, zapewniając jednocześnie możliwość sprawdzenia, czy użytkownik wprowadził poprawne hasło. Następny pomysł, ,,solenie'', rozwiązuje ten problem.

Naprawdę sprytną techniką, która rozwiązuje niektóre problemy z używaniem zwykłego skrótu, jest solenie. Solenie oznacza po prostu dołączenie dodatkowych danych, zwanych solą, na końcu hasła, a następnie haszowanie hasła i soli. Zwykle sól jest dość duża (na przykład 128 bitów). Kiedy użytkownik próbuje się zalogować, musimy znać sól jego hasła, aby można było ją dodać do hasła przed haszowaniem i sprawdzeniem. Początkowo może się to wydawać trudne, ale sól nie powinna być trzymana w sekrecie. Znajomość soli nie pomaga atakującemu w matematycznym odwróceniu hasza i odzyskaniu hasła. Dlatego powszechnie praktykuje się przechowywanie jej w postaci tekstu jawnego w bazie danych.

Gdy użytkownik się rejestruje, generowana jest duża losowa wartość soli, dodawana na koniec hasła, a połączone hasło i sól są haszowane. Tekst jawny soli jest przechowywany obok skrótu.

Jeśli hasła są solone i mieszane, wtedy tęczowa tablica jest bezużyteczna dla atakującego. Przy obecnej mocy obliczeniowej i pamięci nie można generować tabel tęczowych dla wszystkich popularnych haseł ze wszystkimi możliwymi solami. Powoduje to znaczne spowolnienie atakującego, jednak wciąż może on próbować odgadnąć każde hasło, jedno po drugim. Po prostu musi odgadnąć hasła, dodać sól do nich, a następnie sprawdzić, czy hasz jest gdzieś w bazie danych.

Typowym atakiem brutalnym jest atak słownikowy. Atakujący pisze prosty program, który przechodzi długą listę słów ze słownika, innych popularnych haseł i wszystkich kombinacji znaków poniżej pewnej długości. Do każdego wpisu na liście program dodaje sól, a następnie haszuje, aby sprawdzić, czy pasuje to do skrótu, dla którego próbuje ustalić hasło. Dobry sprzęt może sprawdzać miliony, a nawet miliardy wpisów na sekundę. Wiele haseł wybieranych przez użytkowników można odzyskać w czasie krótszym niż sekunda przy użyciu ataku słownikowego.

Niestety, ze szkodą dla użytkowników, wiele firm stara się wyciszyć wycieki baz danych, ponieważ jest to ogromna afera, która może negatywnie wpłynąć na firmę. Czasami firma nie wie, że jej baza danych wyciekła, lub ma podejrzenia, że tak było, ale z powodów wizerunkowych temu zaprzecza. W najlepszym wypadku może cię poprosić o wybranie nowego hasła, jako powód podając niejasne ogólniki. Z tego powodu ważne jest, aby w każdym miejscu używać różnych haseł, aby napastnik nie włamał się na twoje konta w innych witrynach. Prawdopodobnie krążą gdzieś po świecie twoje hasła, o których myślisz, że nikt ich nie zna, ale gdzieś jakiś atakujący uzyskał je z bazy danych do której której się włamał.

Choć w teorii szyfrowanie soli wygląda na dobry sposób na zwiększenie bezpieczeństwa, w praktyce wcale nie jest tak dobrze. Nie możemy użyć jednokierunkowej funkcji skrótu (ponieważ potrzebujemy soli do sprawdzenia hasła), więc zamiast tego musielibyśmy użyć jednej z metod szyfrowania, które poznaliśmy wcześniej, które do deszyfrowania używają tajnego klucza. Ten tajny klucz musiałby być znany programowi który sprawdza hasło (w przeciwnym razie nie mógłby on poznać soli potrzebnych do sprawdzenia haseł!), i musimy założyć, że atakujący również by go zdobył. Najlepszym zabezpieczeniem przed atakami brutalnymi wykonywanymi offline są dobrze wybrane przez użytkowników hasła.

To dlatego strony internetowe wymuszają minimalną długość hasła i często wymagają kombinacji małych i wielkich liter, symboli i cyfr. Istnieje 96 standardowych znaków, których możesz użyć w haśle: 26 wielkich liter, 26 małych liter, 10 cyfr i 34 symboli. Jeśli wybrane hasło jest całkowicie losowe (np. nie są to słowa ani żadne wzorce), każdy dodany znak powoduje, że twoje hasło jest 96 razy trudniejsze do odgadnięcia. 8 do 16 znaków może zapewnić bardzo wysoki poziom bezpieczeństwa, o ile hasło jest naprawdę losowe. Takich właśnie haseł powinieneś używać (i upewnij się, że używasz innego hasła dla każdej witryny!).

Niestety te wymagania nie powodują, że użytkownicy wybierają dobre hasła. Atakujący znają sztuczki, których używają użytkownicy do tworzenia haseł, żeby spełniały wszystkie wymagania, ale żeby było je łatwo zapamiętać. Na przykład P@$$w0rd zawiera 8 znaków (powszechnie używane minimum) i zawiera mieszankę różnych typów znaków. Jednak atakujący wiedzą, że użytkownicy lubią zastępować S za pomocą $, zamieniać o i 0, i na !, itd. Właściwie mogą po prostu dodać te sztuczki do listy, której używają do ataków słownikowych. W przypadku stron internetowych, które wymagają od haseł posiadania co najmniej jednej cyfry, wynik jest jeszcze gorszy. Wielu użytkowników wybiera standardowe polskie słowo, a następnie dodaje jedną cyfrę na końcu. To znowu łatwizna dla ataku słownikowego!

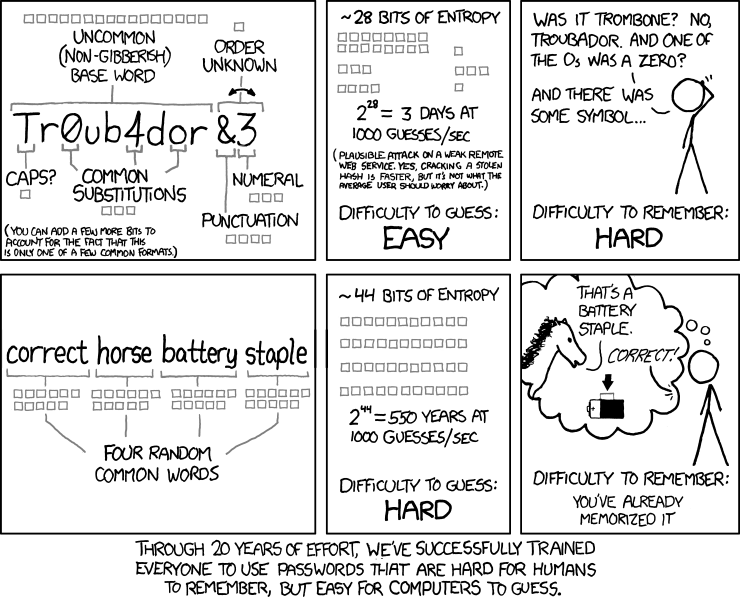
Jak wskazuje ten komiks xkcd, większość porad dotyczących haseł nie ma większego sensu.

Plik źródłowy

Być może nie wiesz, co oznaczają niektóre ze słów. W uproszczeniu, komiks mówi, że jest znacznie mniej modyfikacji popularnych słów słownikowych niż losowych wyborów czterech spośród 2000 najpopularniejszych słów słownikowych. Zauważ, że szacunki szybkości opierają się na próbach odgadnięcia przez system logowania. W przypadku wycieku bazy danych atakujący może przetestować miliardy haseł na sekundę, a nie tylko kilka tysięcy.

Pierwsze przykłady w tym rozdziale wykorzystują bardzo słabe metody szyfrowania, które zostały wybrane w celu zilustrowania pojęć, ale nigdy nie zostałyby użyte w systemach komercyjnych czy wojskowych.

Istnieje wiele aspektów bezpieczeństwa komputera poza szyfrowaniem. Na przykład kontrola dostępu (m.in. systemy haseł i bezpieczeństwo kart inteligentnych) ma kluczowe znaczenie dla zabezpieczenia systemu. Innym poważnym problemem jest pisanie bezpiecznego oprogramowania, które nie daje użytkownikowi możliwości uzyskania dostępu do informacji, których nie powinien poznać (np. przez wpisanie polecenia bazy danych do kwerendy w witrynie, które system przypadkiem uruchomi lub przepełnienie bufora dużą ilością danych wejściowych, które mogą przypadkowo zastąpić części programu). Ponadto, systemy muszą być chronione przed atakami typu ,,zablokowanie usługi'' ("Denial Of Service" -- DOS), gdzie są tak przeładowane żądaniami (np. prośbami o wysłanie strony internetowej, jak przy przeglądaniu), że serwer nie może sobie z nimi poradzić, a uprawnieni użytkownicy otrzymują odpowiedzi bardzo powoli, albo system może nawet całkowicie zawieść.

Jeśli chodzi o inne rodzaje ataków związanych z bezpieczeństwem komputerowym, patrz wpis w angielskiej Wikipedii na temat hakerów.

Nad bezpieczeństwem wszystkich obecnych metod szyfrowania wiszą ciemne chmury: komputery kwantowe. Komputery kwantowe są w powijakach, ale jeśli to podejście do obliczeń okaże się udane, może umożliwić działanie bardzo szybkich algorytmy atakowania naszych najbezpieczniejszych systemów szyfrujących (na przykład mogłoby być użyte do bardzo szybkiego wyznaczania dzielników liczb). W rzeczywistości algorytmy kwantowe zostały już wynalezione, ale nie wiemy, czy można zbudować komputery kwantowe, na których mogłyby one działać. Takie komputery najprawdopodobniej nie pojawią się z dnia na dzień, a jeśli ich budowa stanie się możliwa, otworzą również możliwość stosowania nowych algorytmów szyfrowania. Jest to kolejna zagadka w informatyce -- nie wiemy, co przyniesie przyszłość i gdzie mogą nastąpić poważne zmiany. Ale będziemy potrzebować bardzo zdolnych informatyków do radzenia sobie z takimi zmianami!

Ale jest też dobra strona -- kwantowe protokoły dystrybucji kluczy i są one stosowane w praktyce (przy użyciu specjalistycznego sprzętu do generowania bitów kwantowych); zapewniają one teoretycznie doskonały system szyfrowania i nie polegają na tym, że atakujący nie jest w stanie rozwiązać określonego problemu obliczeniowego. Ze względu na konieczność użycia specjalistycznego sprzętu są one wykorzystywane tylko w środowiskach o wysokim poziomie bezpieczeństwa, takich jak bankowość.

Oczywiście szyfrowanie nie rozwiązuje wszystkich naszych problemów związanych z bezpieczeństwem, a ponieważ są dostępne dobre systemy szyfrowania, złodzieje informacji muszą zastosować inne podejścia, w szczególności inżynierię społeczną. Najłatwiejszym sposobem uzyskania hasła użytkownika jest spytanie go o nie! Atak phishingowy robi właśnie coś takiego, a istnieją szacunki, że aż 1 na 20 użytkowników komputera zdradził kiedyś w ten sposób tajne informacje.

Inne stosowane metody inżynierii społecznej, to przekupywanie lub szantażowanie osób mających dostęp do systemu lub po prostu szukanie hasła zapisanego na karteczce przyklejonej do czyjegoś monitora! Uzyskanie dostępu do czyjegoś konta email jest szczególnie łatwym sposobem na uzyskanie wielu haseł, ponieważ wiele systemów przywracania ,,zgubionego hasła'' wysyła nowe hasło na konto email.

Artykuł o kryptologii w Wikipedii dość przystępnie wyjaśnia terminologię użytą w tym rozdziale.

Obecnie stosowane metody szyfrowania opierają się na dość zaawansowanej matematyce; z tego powodu książki o szyfrowaniu zwykle albo wymagają większej wiedzy niż na poziomie liceum, albo opisują kody, które nie są używane w praktyce.

Istnieje wiele intrygujących historii dotyczących szyfrowania, w tym jego wykorzystania w czasie wojny i do szpiegowania. Oto kilka książek na ten temat:

• David Kahn How I Discovered World War II's Greatest Spy and Other Stories of Intelligence and Code, Auerbach Publications Boston 2014;

• Friedrich L. Bauer Sekrety kryptografii, Helion 2003;

• Craig Bauer Secret History: The Story of Cryptology, CRC Press 2013;

• David Kahn Łamacze kodów. Historia kryptologii, WNT 2004;

• Marek Grajek Enigma. Bliżej prawdy, Rebis 2010;

• Simon Singh Księga Szyfrów, Albatros 2001.

Poniższe ćwiczenia na stronie CS Unplugged pozwalają pobawić się protokołami kryptograficznymi. Są po angielsku, ale posiadają polską instrukcję. Metody szyfrowania w nich użyte nie są wystarczająco mocne, aby można je było wykorzystać w praktyce, ale zapewniają pewien wgląd w to, co jest możliwe:

• Ukrywanie informacji;

• Protokoły kryptograficzne;

• Szyfrowanie z kluczem publicznym.

Artykuł War in the fifth domain o wojnie w cyberprzestrzeni opowiada o tym, jak szyfrowanie i bezpieczeństwo są kluczowe dla naszej obrony.

Istnieje wiele artykułów w CS4FN na temat kryptografii, w tym o ataku statystycznym który doprowadził do... ścięcia głowy.

Książka Hacking Secret Ciphers with Python: A beginner's guide to cryptography and computer programming with Python Ala Sweigarta (CreateSpace Independent Publishing Platform 2013) omawia niektóre proste szyfry, w tym te omówione w tym rozdziale, a także jak można je programować (i atakować) za pomocą programów w języku Python.

• How Stuff Works -- o szyfrowaniu (po angielsku);
• Cryptool to darmowy system pozwalający wypróbowywać klasyczne i nowoczesne metody szyfrowania. Niektóre z nich wykraczają poza zakres tego rozdziału, ale wiele z nich może się przydać do eksperymentowania z kryptografią i prowadzenia demonstracji.
• Wikipedia -- klucze kryptograficzne;
• Wikipedia -- szyfr Cezara;
• filmy o nowoczesnych metodach szyfrowania (po angielsku);
• programy interaktywne z prostymi szyframi (po angielsku).