Kompresja danych zmniejsza miejsce potrzebne do zapisu plików. Jeżeli możesz zmniejszyć o połowę rozmiar pliku, to oznacza, że możesz przechowywać dwa razy więcej plików przy tych samych kosztach, lub możesz ściągać pliki dwa razy szybciej (płacąc dwa razy mniej za transfer). Pomimo tego, iż dyski twarde zwiększają objętość oraz wysoka przepustowość łączy staje się powszechna, to nadal dobrze jest osiągnąć przynajmniej to samo, pracując na mniejszym, skompresowanym pliku. Dla dużych magazynów danych, takich jakie posiadają Google lub Facebook, zmniejszenie o połowę przestrzeni potrzebnej do zapisu oznacza olbrzymie oszczędności w przestrzeni dyskowej, mocy obliczeniowej, a w konsekwencji oszczędności w zużyciu energii, chłodzeniu oraz niepożądanym wpływie na środowisko.
Częste formy kompresji będące aktualnie w użyciu to JPEG (dla zdjęć), MP3 (dla plików audio), MPEG (dla wideo w tym DVD), oraz ZIP (dla dowolnych typów danych). Przykładowo, metoda kompresji JPEG redukuje rozmiar zdjęcia do jednej dziesiątej lub mniejszej części początkowego rozmiaru, co oznacza, iż aparat może przechowywać 10 razy więcej zdjęć, a obrazki w sieci mogą być ściągane 10 razy szybciej.
Na czym polega haczyk? Okazuje się, że może być problem z jakością danych -- np. mocno skompresowany obraz w JPEG może nie być tak ostry jak nieskompresowany oryginał. Poza tym, kompresowanie i dekompresowanie wymaga mocy obliczeniowej procesora. W większości przypadków ten narzut się jednak opłaca.
Przesuń by porównać oba obrazki


55 Kb JPEG
139 Kb JPEG
W tym rozdziale przyjrzymy się temu, jak można uzyskać kompresję, jakie są korzyści i jakie koszty związane z używaniem skompresowanych danych. Będzie to przydatne podczas podejmowania decyzji, czy opłaca się kompresować dane.
Zaczniemy od prostego przykładu – kodowania długości serii (RLE od ang. Run Length Encoding) – które daje pewien wgląd w zalety i wady kompresji.
-
Dla nauczyciela. Zadanie: uwięziony w ciele
Przykładem intrygującego zadania związanego z kompresją jest zadanie „uwięziony w ciele” z CS4FN (po angielsku). W tym zadaniu uczniowie symulują pisanie tekstu metodą używaną przez Jeana-Dominique’a Bauby, który był całkowicie sparaliżowany i mógł poruszać jedynie powieką. Przy pomocy prostego binarnego interfejsu (miga lub nie miga) był w stanie podyktować całą książkę. Warto dobrać uczniów w pary i kazać im spróbować porozumiewać się jedynie mrugając. Zadanie to sprowokuje uczniów do zastanowienia się, jak robić to w najkrótszym czasie i przy najmniejszym wysiłku. Oczywiście, w pierwszym kroku będą musieli ustalić jak przekazać jakąkolwiek treść w ten sposób.
Kodowanie długości serii (RLE od ang. Run Length Encoding) nie jest techniką często używaną współcześnie, ale nadaje się świetnie jako wprowadzenie do problemów związanych z kompresją.
-
Dla nauczyciela. Kto korzysta z kodowania długości serii?
Kodowanie długości serii było w powszechnym użyciu kiedy normą były czarno-białe obrazy. To właśnie ten typ kompresji umożliwił standaryzację w 1980 r. transmisji danych za pomocą faksu. Piksele w przesyłanym faksem obrazie był jedynie czarne lub białe charakteryzowały się przeważnie długimi ciągami białych pikseli na marginesach, co sprawiało, że RLE było wyjątkowo skuteczne. Poza tym metoda ta była bardzo prosta, co było ważne w roku 1980, gdyż pozwoliło znacznie obniżyć koszt elektroniki w urządzeniu.
Kodowanie długości serii jest nadal używane jako część kompresji JPEG, jednakże nie do kodowania ciągu pikseli (w fotografii rzadko występują ciągi pikseli o dokładnie takim samym kolorze).
Opowiadamy o RLE, gdyż ilustruje praktycznye podejście do kompresji i, co ważniejsze pokazuje kluczowe zalety i problemy związane z kompresją.
Wyobraźmy sobie, że mamy do czynienia z zamieszczonym poniżej prostym obrazkiem.
Komputer może w prosty sposób zapisać taki obrazek stosując format, w którym zero oznacza piksel w kolorze białym, a jedynka -- piksel w kolorze czarnym (jest to „mapa bitowa”, gdyż przypisaliśmy pikselom wartości bitów). Używając tej metody powyższy obrazek przedstawimy w następujący sposób:
011000010000110
100000111000001
000001111100000
000011111110000
000111111111000
001111101111100
011111000111110
111110000011111
011111000111110
001111101111100
000111111111000
000011111110000
000001111100000
100000111000001
011000010000110
-
Ciekawostka. Format pliku PBM
Istnieje format obrazu, który wykorzystuje prostą reprezentację, w której jeden symbol odpowiada jednemu bitowi. Ten format nazywa się przenośnym formatem mapy bitowej PBM (ang. portable bitmap format). Pliki PBM są zapisywane z rozszerzeniem .pbm, i zawierają prosty nagłówek, za którym zapisane są dane obrazu. Dane w tym pliku można obejrzeć otwierając go w edytorze tekstowym, podobnie jak plik .txt, a sam obrazek możemy zobaczyć otwierając w programie graficznym, który wspiera format PBM (format ten nie jest szeroko wspierany, ale istnieje kilka programów go obsługujących) Plik pbm dla obrazu zawierającego wcześniej przywołany kształt diamentu wygląda następująco:
P1 15 15 011000010000110 100000111000001 000001111100000 000011111110000 000111111111000 001111101111100 011111000111110 111110000011111 011111000111110 001111101111100 000111111111000 000011111110000 000001111100000 100000111000001 011000010000110Pierwsze dwa wiersze stanowią nagłówek. Pierwszy wiersz określa format danych w pliku (P1 oznacza, że plik zawiera znaki zer i jedynek w formacie ASCII). Drugi wiersz wyznacza szerokość i wysokość obrazu w pikselach. Dzięki temu komputer zna wymiary obrazu nawet wtedy, gdy brakuje znaków nowego wiersza. Resztę danych stanowi po prostu obraz (patrz powyżej). Można skopiować i wkleić tę reprezentację (wraz z nagłówkiem) do pliku tekstowego, a następnie zapisać z rozszerzeniem .pbm. Jeśli posiadasz program, który obsługuje pliki PBM, może zobaczyć obraz. Mógłbyś również napisać program, który będzie pozwalał tworzyć tego typu pliki oraz wyświetlać je jako obrazy.
Z tego względu, iż cyfry są reprezentowane przez znaki ASCII, nie jest to najbardziej efektywny sposób zapisu. Jednakże możemy przeczytać zawartość pliku. Istnieją inne warianty tego formatu, które zapisują kolory w pojedynczych bitach zamiast w znakach ASCII, oraz takie, które umożliwiają zapis odcieni szarości lub kolorów. Więcej informacji na temat tego formatu dostępnych jest w angielskiej Wikipedii.
Kluczowym pytaniem w przypadku kompresji jest: Czy możemy zapisać obraz przy pomocy mniejszej ilości bitów i nadal być w stanie go odtworzyć?
Okazuje się, że możemy. Jest wiele sposobów na osiągnięcie tego celu, ale w tym podrozdziale skupimy się na metodzie zwanej kodowaniem długości serii.
Wyobraź sobie, że masz za zadanie przeczytać powyższe bity komuś, kto z kolei ma je zapisać. Po pewnej chwili będziesz mówił „pięć zer” zamiast „zero zero zero zero zero”. To usprawnienie jest podstawą kodowania długości serii (RLE), które pozwala zaoszczędzić przestrzeń potrzebną do przechowywania cyfrowych obrazów. W kodowaniu długości serii zastępujemy każdy wiersz liczbą kolejnych pikseli tego samego koloru, zawsze zaczynając od liczby pikseli białych. W omówiony wyżej przykładzie pierwszy wiersz zawiera jeden biały, dwa czarne, cztery białe, jedne czarny, cztery białe, dwa czarne i jeden biały piksel.
011000010000110
Możemy to przedstawić w następujący sposób.
1, 2, 4, 1, 4, 2, 1
W przypadku drugiego wiersza, który zaczyna się pikselem czarnym, mówimy, że jest zero białych na początku.
100000111000001
0, 1, 5, 3, 5, 1
Może to wydawać się dziwne, że musimy podać zawsze liczbę białych na początku, która w tym wypadku wynosi zero. Powodem tego jest fakt, iż komputer potrzebuje ścisłych reguł odnośnie tego, od którego koloru pikseli zaczynać.
Trzeci wiersz zawiera pięć białych, pięć czarnych, oraz pięć białych pikseli.
000001111100000
To jest kodowane jako:
5, 5, 5
Zatem mamy następującą reprezentacją dla pierwszych trzech wierszy pikseli obrazu.
1, 2, 4, 1, 4, 2, 1
0, 1, 5, 3, 5, 1
5, 5, 5
Łatwo można się domyślić jak będą wyglądać kolejne wiersze w tym systemie reprezentacji.
-
Spojler. Reprezentacja pozostałych wierszy
Pozostałe wiersze to:
4, 7, 4 3, 9, 3 2, 5, 1, 5, 2 1, 5, 3, 5, 1 0, 5, 5, 5 1, 5, 3, 5, 1 2, 5, 1, 5, 2 3, 9, 3 4, 7, 4 5, 5, 5 0, 1, 5, 3, 5, 1 1, 2, 4, 1, 4, 2, 1
-
Ciekawostka. Kodowanie długości serii w programie „Informatyka bez komputera”
W poniższym materiale wideo z programu „Informatyka bez komputera” zakodowany przy pomocy długości serii obraz jest odkodowany i zaprezentowany przez bardzo duże piksele (drukarką jest farba w sprayu!).
Aby upewnić się, że możemy odwrócić proces kompresji, spróbuj znaleźć oryginalną reprezentację (zera i jedynki) skompresowanego obrazu.
4, 11, 3
4, 9, 2, 1, 2
4, 9, 2, 1, 2
4, 11, 3
4, 9, 5
4, 9, 5
5, 7, 6
0, 17, 1
1, 15, 2
Co zawiera obraz? Z jak wielu pikseli się składa? Ile liczb użyto do reprezentacji tego obrazu?
-
Spojler. Odpowiedź dla powyższego obrazu
Rozwiązaniem jest filiżanka i talerzyk. Obrazek pochodzi z ćwiczenia interaktywnego Reprezentacja obrazów. Strona jest po angielsku, ale jest polska instrukcja do ćwiczenia.
Poniższa aplikacja umożliwia dalsze eksperymentowanie z kodowaniem długości serii.
Jak wiele przestrzeni zaoszczędziliśmy wykorzystując alternatywną reprezentację, i jak możemy to zmierzyć? W tym celu możemy policzyć ile razy musieliśmy nacisnąć przycisk na klawiaturze zapisując każdą z reprezentacji, zakładając, że każdy bit to jeden znak oraz, że każda cyfra i przecinek kodu RLE wymagają również znaku przy zapisie (to zgrubne oszacowanie na początek wystarczy).
Aby opisać obraz z naszego przykładu w postaci nieskompresowanej potrzebnych jest 225 cyfr (zer i jedynek). Policz ile potrzeba przecinków i cyfr (pomiń spacje i znaki nowego wiersza) w nowej reprezentacji. Innymi słowy, policz znaki potrzebne do zapisania skompresowanej reprezentacji (abyś miał pewność, że wiesz o co chodzi, podajemy ci liczbę znaków w każdym z trzech pierwszych wierszy: 29).
Powinieneś otrzymać wynik 119 znaków (sprawdź, czy wszystko się zgadza). Oznacza to, że skompresowana postać wymaga jedynie 53% znaków reprezentacji oryginalnej (wynika to z proporcji 119/225). To znacząca redukcja w wielkości przestrzeni potrzebnej do zapisania obrazu -- to prawie połowa rozmiaru. Nowa reprezentacja jest skompresowaną postacią poprzedniej.
-
Dla ciekawych. Kodowanie długości serii w praktyce
W praktyce metoda ta (z pewnymi modyfikacjami) może być użyta do osiągnięcia kompresji na poziomie 15% oryginalnego rozmiaru. W rzeczywistych systemach tylko jeden bit jest wykorzystywany do przechowywania wartości czarno/białe (w przeciwieństwie do jednego znaku z naszych obliczeń). Jednakże długości kodowanych serii są również przechowywane bardziej efektywnie, również przy pomocy bitów, których stosunkowo krótkie ciągi mogą reprezentować liczby. Wykorzystywane ciągi bitów są tworzone przy pomocy techniki zwanej kodowaniem Huffmana, lecz zagadnienie to wykracza poza zakres tego materiału.
Współcześnie głównym zastosowaniem dla skanowanych czarno-białych obrazów są faksy, które wykorzystują RLE. Jednym z powodów, dla których działa to tak skutecznie dla skanowanych stron dokumentów jest fakt, iż w tym przypadku liczba kolejnych białych pikseli jest olbrzymia. Typowa strona przesyłana faksem ma 200 pikseli szerokości, więc zastąpienie tych 200 bitów liczbą jest znaczącą oszczędnością. Z kolei liczbę tę możemy wyrazić przy pomocy zaledwie kilku bitów. Choć może się zdarzyć, że liczbą zastępujemy krótką serię pikseli, to i tak w ostatecznym rozrachunku oszczędności są znaczące. W praktyce faksy, które nie korzystają z kompresji, przesyłają dokumenty 7 razy wolniej.
-
Projekt. Zastosuj kodowanie długości serii
Teraz, gdy już znasz kodowanie długości serii, możesz sam stworzyć obraz czarno-biały, a następnie go skompresować, oraz zdekompresować obraz otrzymany od kogoś innego.
Zacznij od narysowania obrazu przy pomocy zer i jedynek. (Upewnij się, że jest prostokątny, tzn. wszystkie wiersze mają tę samą długość.) Możesz go narysować na papierze lub przygotować na komputerze (korzystaj z czcionki o stałej szerokości, w przeciwnym wypadku może to okazać się frustrujące i kłopotliwe!) Ułatwieniem może być skorzystanie z kartki w kratkę (takiej jak w zeszycie do matematyki), zakreślenie kratek mających być czarnymi pikselami i pozostawienie pustych kratek jako pikseli białych. Po zakończeniu tej czynności możesz spisać zera i jedynki reprezentujące obraz.
Stwórz skompresowaną reprezentację twojego obrazu stosując metodę kodowania długości serii, tzn. długości serii oddzielone przecinkami jak zostało przestawione powyżej.
Przekaż kopię skompresowanej reprezentacji (długości serii, nie oryginalną reprezentację zerojedynkową) koledze oraz wytłumacz mu na czym polegała kompresja. Poproś go o narysowanie obrazu na kartce w kratkę. Następnie porównaj otrzymany obrazek z twoim oryginałem.
Wyobraź sobie, że ty i twój kolega, oboje jesteście komputerami. Wykonując powyższe zadanie pokazałeś, że obrazy mogą zostać skompresowane na jednym komputerze i zdekompresowane na innym, tak długo jak istnieje uzgodniony standard (np. to, że każdy wiersz zaczyna się od liczby białych pikseli). W przypadku algorytmów kompresji bardzo istotne jest trzymanie się standardów, tak aby po skompresowaniu na jednym komputerze możliwa była dekompresja na innym. Przykładowo, utwory muzyczne zapisywane są w formacie MP3, aby po pobraniu z sieci mogły być odtworzone przez szeroką gamę urządzeń.
O kompresji bezstratnej mówimy, jeżeli skompresowana reprezentacja może zostać przekonwertowana podczas dekompresji do dokładnie takiej samej postaci jak reprezentacja oryginalna, innymi słowy żadna informacja nie została stracona podczas kompresji i proces ten może być w pełni odwrócony.
Nie wszystkie algorytmy kompresji są jednak bezstratne. Dla niektórych typów plików takich jak zdjęcia, utwory muzyczne i materiały wideo, możemy poświęcić nieco jakości (ilości informacji o zdjęciu), jeśli pozwoli to zmniejszyć znacząco rozmiar pliku. Zmniejszenie rozmiaru plików może mieć olbrzymie znaczenie przy pobieraniu plików tak dużych jak pliki wideo, które mogą być zbyt duże, aby dało się je ściągnąć! Te metody kompresji nazywa się stratnymi. Jeśli tracimy informacje w procesie kompresji, to niemożliwe jest odtworzenie dokładnie takiej samej postaci, jaką miał plik przed kompresją. Jednocześnie osoba, która ogląda plik wideo lub słucha muzyki może zaakceptować nieco pogorszoną jakość jeśli pliki są względnie małe. W dalszej części tego rozdziału zbadamy jaki wpływ na obraz i dźwięk może mieć stratna kompresja.
Co ciekawe, może się wyjątkowo zdarzyć, że skompresowany stratnie plik będzie miał większy rozmiar niż nieskompresowany! Co więcej, naukowcy zajmujący się kompresją udowodnili, iż niemożliwe jest stworzenie metody kompresji bezstratnej, która zmniejsza każdy plik. W zdecydowanej większości przypadków nie jest to problemem, gdyż stratne metody kompresji dostosowane są do pewnych rodzajów danych, posiadających pewną charakterystykę, dla których nieskuteczna kompresja jest wysoce nieprawdopodobna.
-
Wyzwanie. Najlepsze i najgorsze przypadki dla kodowania długości serii
Jaki obraz będzie miał największy stopień kompresji przy kodowaniu długości serii (chodzi o obraz, którego rozmiar po skompresowaniu będzie najmniejszy w stosunku do rozmiaru początkowego)? Jest to przypadek, w którym wydajność algorytmu jest najwyższa.
Kiedy kompresja jest najgorsza? Czy potrafisz znaleźć obraz, który ma większą reprezentację skompresowaną? (Pamiętaj o przecinkach, którymi oddzielamy długości serii!) Jest to przypadek, w którym wydajność algorytmu jest najgorsza.
-
Spojler. Rozwiązanie zadania
Najlepszy przypadek jest wtedy, gdy obraz jest całkowicie biały (wystarczy jedna liczba na wiersz). Najgorszy przypadek ma miejsce, gdy na zmianę występują piksele białe i czarne.
-
Ciekawostka. Kompresja może powiększać pliki
W najgorszym przypadku (na zmianę piksele białe i czarne) kodowanie długości serii da nam plik skompresowany o rozmiarze większym niż plik oryginalny! Jak został wspomniane wcześniej, każdy bezstratny algorytm kompresji, który przynajmniej jeden plik zmniejsza, musi mieć kilka plików, które powiększa -- nie jest matematycznie możliwe, aby stworzyć algorytm kompresji bezstratnej, który zmniejsza każdy plik. Jako trywialny przykład posłuży nam pewna kompresja plików z 3-bitowych do 2-bitowych. Ile jest plików 3-bitowych? (Jest ich 8.) Ile jest plików 2-bitowych (Są ich 4.) Czy widzisz problem? Mamy 8 plików, które możemy chcieć skompresować, ale jednocześnie tylko 4 sposoby na ich reprezentację. Zatem niektóre z nich będą miały taką samą reprezentację, a przez to nie mogą zostać odkodowane dokładnie.
Na przestrzeni lat było kilka oszustw opartych na twierdzeniach o bezstratnej metodzie kompresji, która kompresuje każdy plik. Skompresować każdy plik do mniejszego można tylko metodą stratną (czyli tracąc informacje); wszystkie metody bezstratne muszą powiększać niektóre pliki. Dobrze byłoby mieć metodę, która kompresuje wszystkie pliki bez strat; można by wtedy skompresować duży plik, a następnie zastosować kompresję do skompresowanego pliku i zmniejszyć go ponownie, powtarzając aż do uzyskanie jednego bajtu -- lub jednego bitu! Niestety nie jest to możliwe.
Obrazy mogą zajmować dużo miejsca, dlatego najczęściej obrazy są przechowywane na komputerze w postaci skompresowanej. Pozwala to zaoszczędzić miejsce na dysku. Najczęściej, zwłaszcza w przypadku zdjęć, nie ma potrzeby przechowywania obrazu dokładnie tak, jak wyglądał on pierwotnie. Wynika to z faktu, iż zawiera on więcej szczegółów niż ktokolwiek może zobaczyć. W rezultacie możemy zaoszczędzić przestrzeń dyskową, zwłaszcza jeśli utracone szczegóły są trudno dostrzegalne dla ludzkiego oka. Istnieją inne sytuacje, w których obrazy muszą być przechowywane w dokładnie takiej samej postaci jak oryginał, na przykład w przypadku skanów medycznych lub przetwarzania zdjęć o bardzo wysokiej jakości. W takich przypadkach stosuje się metody bezstratne lub obrazy nie są w ogóle kompresowane (np. w formacie RAW na aparatach).
W podrozdziale o reprezentacji danych sprawdziliśmy, jak można zmniejszyć rozmiar pliku obrazu, używając mniejszej liczby bitów do opisania koloru każdego piksela. Jednak metody kompresji obrazu, takie jak JPEG, wykorzystują wzorce w obrazie, aby zmniejszyć przestrzeń potrzebną do jego przedstawienia, bez niekorzystnego wpływu na obraz.
Poniższe trzy obrazy pokazują różnicę między zmniejszeniem głębi bitowej a użyciem wyspecjalizowanego systemu kompresji obrazu. Obraz po lewej stronie jest oryginałem, który używa 24 bity na piksel. Środkowy obraz został skompresowany do jednej trzeciej oryginalnego rozmiaru za pomocą JPEG; pomimo, iż jest to „stratna” wersja oryginału, różnica nie jest widoczna. Obraz po prawej stronie ma liczbę kolorów zmniejszoną do 256, a więc używa 8 bitów na piksel zamiast 24, co oznacza, że zajmuje jedną trzecią pierwotnego rozmiaru. Mimo że stracił tyle samo bitów, usunięte informacje miały znacznie większy wpływ na to, jak wygląda. Na tym polega zaleta formatu JPEG: usuwa informacje z obrazu, które nie mają dużego wpływu na postrzeganą jakość. Ponadto w przypadku formatu JPEG można ustalić kompromis między jakością a rozmiarem pliku.
Zmniejszenie liczby bitów (głębia kolorów) jest na tyle istotną zmianą, że nie uważamy tego za metodę kompresji, lecz po prostu za reprezentację niskiej jakości. Metody kompresji obrazu, takie jak JPEG, GIF i PNG, zostały zaprojektowane tak, aby wykorzystać wzorce w obrazie, w celu uzyskania znacznej redukcji rozmiaru pliku bez znaczącej utraty jakości.
Na przykład poniższy obraz pokazuje powiększone piksele, które są fragmentem oka z powyższego obrazu (wysokiej jakości).
Zauważmy, że kolory sąsiednich pikseli są często bardzo podobne, nawet w tej części obrazu, która ma dużo szczegółów. Na przykład piksele pokazane w czerwonym polu poniżej zmieniają się stopniowo z bardzo ciemnego na bardzo jasny.
Kodowanie długości serii nie działa w tym przypadku. Można by skorzystać z wariantu, który określa kolor piksela, a następnie mówi, ile kolejnych pikseli ma ten sam kolor. Chociaż większość sąsiednich pikseli jest prawie taka sama, to szanse na to, że są identyczne, są bardzo niskie, a serie identycznych kolorów prawie nie występują.
Istnieje jednak sposób, aby wykorzystać stopniowo zmieniające się kolory. W przypadku pikseli w czerwonym polu powyżej, możesz wygenerować przybliżoną wersję tych kolorów, określając tylko pierwszy i ostatni w serii. Na tej podstawie komputer będzie obliczać pośrednie, zakładając, że kolor zmienia się stopniowo. Zamiast zapisywania wartości dla 5 pikseli otoczonych na powyższym rysunku czerwoną ramką, wystarczy zapisać tylko dwie wartości, aby oglądający nie zauważył żadnej różnicy. Jest to stratne, ponieważ nie można dokładnie odtworzyć oryginału, ale wystarczająco dobre dla wielu zastosowań i pozwalające zaoszczędzić dużo miejsca.
-
Co to jest?. Interpolacja
Proces zgadywania kolorów pikseli między dwoma, które są znane, jest przykładem interpolacji. Interpolacja liniowa zakłada, że wartości rosną o stałą wielkość pomiędzy dwiema podanymi wartościami. Na przykład, dla pięciu powyższych pikseli załóżmy, że pierwszy piksel ma wartość koloru niebieskiego równą 124, a ostatni ma niebieską wartość 136. W takim przypadku interpolacja liniowa domyślałaby się, że niebieskie wartości dla tych pośrednich wynoszą 127, 130 i 133, a dzięki temu nie trzeba ich zapisywać i można zaoszczędzić miejsce. W praktyce stosuje się bardziej złożone podejście do odgadywania pikseli, ale interpolacja liniowa daje dobre wyobrażenie o tym, jak to działa.
System JPEG, który jest szeroko stosowany do zdjęć, wykorzystuje bardziej wyrafinowaną wersję tego pomysłu. Zamiast działać na pięciu kolejnych pikselach, tak jak to zrobiliśmy powyżej, działa na bloku o rozmiarze 8 na 8 pikseli. Zamiast szacować wartości za pomocą funkcji liniowej, wykorzystuje kombinacje funkcji cosinus.
-
Dla ciekawych. Czym są funkcje sinus i consinus
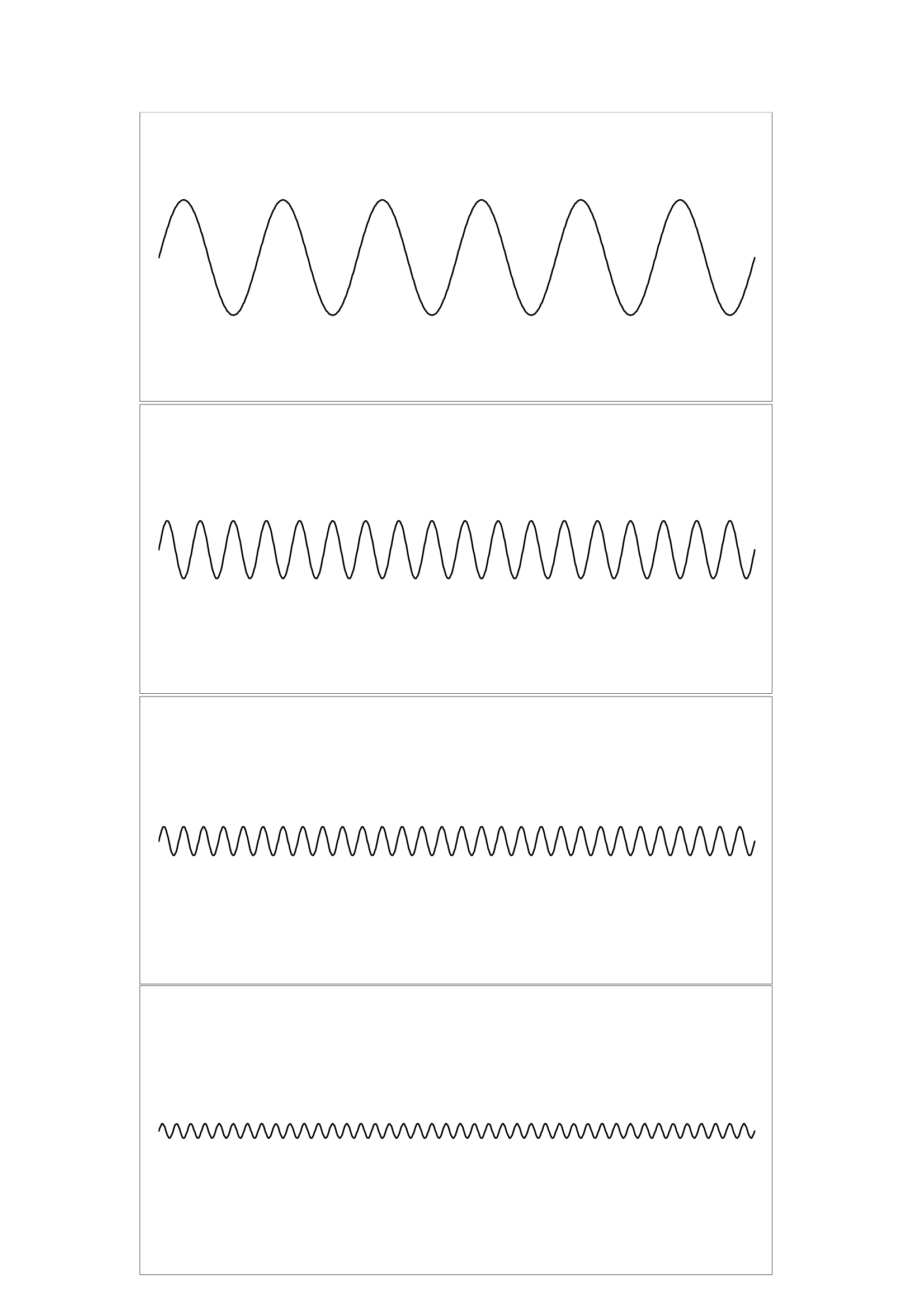
Funkcje sinus i cosinus są funkcjami trygonometrycznymi, które są często używane do obliczania długości boków trójkąta. Wykres wartość sinusa od 0 do 180 stopni jest gładką krzywą o wartościach w przedziale 1 do -1, przypominającą falę (podobnie jak wykres funkcji cosinus, który jest nieco przesunięty). Różne postacie tego wykresu można wykorzystać do przybliżenia wartości pikseli przechodzących z jednego koloru do drugiego. Jeśli dodasz dwie fale cosinusowe o różnych częstotliwościach, to możesz uzyskać interesujące kształty. Teoretycznie każdy wzór złożony z pikseli może zostać utworzony przez dodanie różnych fal cosinusowych!
Poniższy wykres pokazuje wartości funkcji \(\sin(x)\) oraz \(\cos(x)\) dla \(x\) z zakresu od 0 do 180 stopni.
-
Dla ciekawych. Dodawanie fal sinusa i cosinusa w celu uzyskania dowolnego kształtu fali
Metody JPEG (i MP3) bazują na technice, która falę dowolnego kształtu przedstawia jako sumę wielu fal. Przekształcenie kształtu fali dla bloku pikseli lub próbki muzyki w sumę prostych fal można wykonać za pomocą techniki zwanej transformacją Fouriera, która jest powszechnie wykorzystywana przy przetwarzaniu obrazu.
Możesz poeksperymentować z dodawaniem fal, aby uzyskać inne kształty za pomocą udostępnionego arkusza kalkulacyjnego. W arkuszu tym za pomocą żółtego obszaru na pierwszej zakładce możesz wybrać, które fale dodać. Spróbuj ustawić 4 sinusoidy na częstotliwości, które wynoszą odpowiednio 3, 9, 15 i 21 razy częstotliwość podstawowa („podstawowa” to najniższa częstotliwość.) Następnie ustaw „amplitudy” (odpowiednik poziomu głośności) tej czwórki na wartości 0,5, 0,25, 0,125 i 0,0625 (każda z nich jest równa połowie poprzedniej). W rezultacie powinieneś uzyskać poniższe cztery sinusoidy:
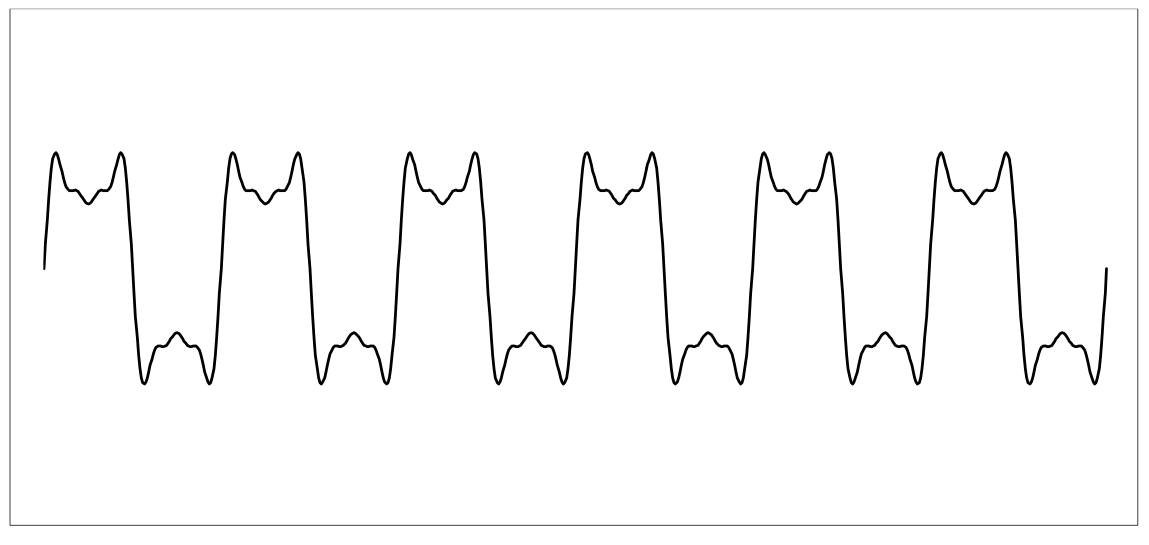
Kiedy powyższe cztery fale są ze sobą dodane, interferują i tworzą kształt, który ma ostrzejsze przejścia:
Okazuje się, że gdyby kontynuować ten wzorzec z większą liczbą sinusoid, kształt wynikowy stałby się „falą prostokątną”, która nagle przechodzi od wartości maksymalnej do minimum. Ta pokazana powyżej jest wyboista, gdyż wykorzystaliśmy tylko 4 fale sinusoidalne, aby ją opisać.
To właśnie dzieje się w algorytmie JPEG, jeśli kompresujesz czarno-biały obraz. „Kolor” pikseli w miarę przesuwania się po obrazie będzie wynosił 0 (czarny) lub pełny poziom intensywności (biały), lecz JPEG będzie przybliżał go za pomocą sumy niewielkiej liczby fal cosinusów (które mają taki sam kształt jak sinusoidy) Daje to „przedobrzenia” widoczne na poniższym obrazku; w obrazie JPEG pojawiają się one jako jasne i ciemne plamy otaczające nagłą zmianę koloru:
Możesz eksperymentować z różnymi kombinacjami fal, uzyskując różne kształty. Być może trzeba mieć więcej niż cztery, aby uzyskać dobre przybliżenia kształtu, który chcesz osiągnąć; to jest właśnie kompromis, z którym stara sobie radzić algorytm JPEG. Na drugiej zakładce arkusza kalkulacyjnego zamieszczone zostały pewne sugestie dotyczące parametrów.
Możesz zapoznać się z przekształceniami Fouriera za pomocą darmowego oprogramowania Wolfram Alpha; będzie to wymagało instalacji wtyczki w przeglądarce. Oto przykładowe prezentacje Wolfram (po ang.): interaktywny pokaz kompresji JPEG, prezentacja związków między sinusoidami a innymi formami falowymi oraz prezentacja tego jak sinusoidy można zsumować, aby otrzymać inne kształty.
Warto przyjrzeć się z bliska mocno skompresowanemu obrazowi JPEG. Na przykład następujący obraz został bardzo mocno skompresowany przy użyciu JPEG (zajmuje jedynie 1,5% pierwotnego rozmiaru).
Jeśli powiększymy obszar oka, wyraźnie widać bloki 8 x 8 pikseli:
Zauważ, iż w każdym bloku występuje bardzo niewielka różnorodność. Na poniższym obrazie blok w czerwonej ramce zmienia się tylko w kierunku pionowym. Prawdopodobnie można go określić, podając tylko dwie wartości brzegowe, pozostałe mogą być wyliczone przez dekoder podobnie jak w przykładzie interpolacyjnym. Zielony kwadrat zmienia się tylko w poziomie i podobnie można go wyrazić przy pomocy dwóch wartości brzegowych zamiast 64 wartości. Niebieski blok ma tylko jeden kolor! Żółty blok jest bardziej skomplikowany, ponieważ w tej części obrazu więcej się dzieje. Pojawiają się tu fale. Od lewej do prawej widzimy zmianę jasności od ciemnej, przez jaśniejszą, do ciemniej, dlatego zmienność tę będzie wygodnie zapisać za pomocą fali. Od góry do dołu żółty zmienia się głównie od jasnego do ciemnego. Dzięki temu możemy przechowywać tylko kilka wartości zamiast wszystkich 64.
Pomimo tego, że jakość jest dość niska, to oszczędność w przestrzeni dyskowej jest ogromna -- plik JPEG jest 60 razy mniejszy (mógłby zostać pobrany 60 razy szybciej). Obrazy JPEG o wyższej jakości przechowują więcej szczegółów dla każdego bloku 8 na 8, co sprawia, że odwzorowują wierniej oryginalny obraz. Zajmują też więcej miejsca, ponieważ zawierają informację o większej liczbie szczegółów. Możesz samemu przetestować jak to wszystko działa, wybierając stopień kompresji w czasie zapisywania pliku w formacie JPEG (większość edytorów graficznych na to pozwala).
-
Co to jest?. Nazwa JPEG
Nazwa jpg jest skrótem od Joint Photographic Experts Group, komitetu utworzonego w latach 80. w celu wypracowania standardów umożliwiających zachowywanie fotografii cyfrowych i wyświetlanie ich na różnych urządzeniach. Ponieważ niektóre systemy operacyjne ograniczają rozszerzenia plików do trzech znaków, pliki skompresowane JPEG mają rozszerzenie .jpg.
-
Dla ciekawych. Więcej na temat fal cosinusowych
Fale cosinusowe wykorzystywane w metodzie JPEG oparte są na dyskretnej transformacji cosinusowej. „Dyskretna” oznacza, że opisujemy ją za pomocą zbioru skończonego. Fale w JPEG są reprezentowane jako wartości dla 8 x 8 punktów (dla kodowanego bloku), a każda z tych wartości pochodzi ze skończonego zbioru liczb binarnych.
Nasuwa się naturalne pytanie, jak metoda JPEG, zaprojektowana do przedstawiania obrazów o płynnie zmieniających się kolorach, działa w sytuacji, gdy kolory zmieniają się nagle? W takim przypadku konieczne jest dodawanie wielu fal, pozwalających uzyskać nagłą zmianę koloru, a tym samym ostrą krawędź. Niestety wtedy fale cosinusowe powodują przesadzone zmiany (zabrudzone krawędzie), takie jak te na drugim z poniższych obrazków, będącym powiększonym fragmentem pierwszego.
Oryginał miał ostre krawędzie, ale na powiększeniu obrazu JPEG widać, że nie tylko krawędzie są rozmyte, ale niektóre ciemniejsze piksele pojawiają się dalej również na białym tle, wyglądając trochę jak cienie lub echa.
Z tego względu JPEG jest używany do kompresji zdjęć i naturalnych obrazów, natomiast inne metody kompresji (takie jak GIF i PNG, które poznamy w dalszej części) będą działać lepiej w przypadku sztucznych obrazów, takich jak ten.
Metody kompresji ogólnego przeznaczenia muszą być bezstratne, ponieważ nie można założyć, że użytkownik zgodzi się na utratę danych. Najbardziej popularne algorytmy tego typu (takie jak ZIP, gzip i rar) oparte są na metodzie zwanej kodowaniem Ziva-Lempela, wymyślonej przez Jacoba Ziva i Abrahama Lempela w latach siedemdziesiątych.
Przyjrzymy się temu zagadnieniu na przykładzie pliku tekstowego. Główną ideą kodowania Ziva-Lempela jest zastępowanie sekwencji znaków często występujących w plikach (na przykład sekwencja znaków „obraz” pojawia się często w tym rozdziale) odnośnikami do miejsca, w którym ostatnio się pojawił. Pod warunkiem, że odniesienie jest mniejsze niż zastępowana fraza, oszczędzamy miejsce. Zwykle systemy oparte na tym podejściu można wykorzystać do zredukowania plików tekstowych do zaledwie jednej czwartej ich oryginalnego rozmiaru, co nie ustepuje prawie żadnej znanej metodzie kompresowania tekstu.
Poniższa aplikacja umożliwia zapoznanie się z tą ideą. Możesz kliknąć pole, aby zobaczyć, dokąd prowadzi odnośnik, a następnie wpisać odpowiednie znaki i w rezultacie odkodować tekst. Co się stanie, jeśli odniesienie wskazuje na inne odniesienie? Jeśli dekodujesz tekst od początku odnośnik będą zawsze wskazywać na odkodowane już znaki i nie będzie problemu z odkodowywaniem.
Możesz wprowadzić własny tekst, klikając zakładkę TEXT. Możesz również wkleić jakiś własny tekst, aby sprawdzić, ile znaków można zastąpić odniesieniami.
Odnośniki są w rzeczywistości dwiema liczbami: pierwsza określa, ile znaków wcześniej zaczyna się sekwencja, a druga -- jaka jest jej długość. Każde takie odwołanie zwykle zajmuje około jednego lub dwóch znaków, więc oszczędzamy miejsce jeżeli zastępowane są co najmniej dwa znaki. Opcje w powyższej aplikacji wymuszają, aby zastępowane sekwencje miały długość większą lub równą 2. Oczywiście bierzemy pod uwagę wszystkie znaki, a nie tylko litery alfabetu, więc system kompresji może również odnosić się do spacji między wyrazami. W praktyce jedną z najczęściej występujących sekwencji jest kropka, po której następuje spacja.
To podejście sprawdzi się również w przypadku obrazów czarno-białych, ponieważ sekwencje takie jak „10 białych pikseli” prawdopodobnie się powtarzają. Oto niektóre fragmenty z wcześniejszego przykładu; możesz wkleić je do powyższej aplikacji, aby zobaczyć, jak działa kompresja.
011000010000110
100000111000001
000001111100000
000011111110000
000111111111000
001111101111100
011111000111110
111110000011111
Powyższy przykład dobrze ilustruje, co dzieje się z obrazami podczas zapisu w formacie GIF lub PNG; wartości pikseli są kompresowane za pomocą algorytmu Ziva-Lempela, który działa dobrze, jeśli wiele kolejnych pikseli ma ten sam kolor. Ale działa bardzo słabo w przypadku zdjęć, w których mało prawdopodobne jest powtórzenie wzorców pikseli.
-
Dla nauczyciela. Ćwiczenie metody Ziva-Lempela
Na stronie CS Unplugged znajduje się ćwiczenie oraz informacje na temat metody Ziva-Lempela, również strona „Computing Science Inside” zawiera ćwiczenia dotyczące tego zagadnienia. Strona CS4FN omawia podobną, nieco prostszą metodę, która nie jest zbyt praktyczna.
-
Ciekawostka. Kompresja ZL lub LZ?
Opisany powyżej algorytm został nazwany kompresją Ziva-Lempela od nazwisk dwóch informatyków, Jacoba Ziva i Abrahama Lempela, którzy wymyślili go w latach siedemdziesiątych. Niestety ktoś pomieszał kolejność autorów, kiedy opisywał ten pomysł i nazwał go kompresją „LZ” zamiast kompresji „ZL”. Wielu naukowców skopiowało błąd, przez co metoda Ziva i Lempela jest obecnie zwana „kompresją LZ”!
Jedną z najczęściej stosowanych metod kompresji muzyki jest MP3, który jest częścią standardu kompresji wideo o nazwie MPEG (Moving Picture Experts Group).
-
Ciekawostka. Nazwa *mp3*
Nazwa mp3 nie jest zbyt oczywista. Pomimo tego, że mp oznacza „ruchomy obraz” (ang. moving picture), a 3 pojawiło się już w pierwszej wersji, to pliki mp3 są używane do zapisu muzyki!
Pełna nazwa standardu, z którego pochodzi MP3, to MPEG, a brakujące „EG” oznacza „grupę ekspertów” (ang. expert group), podobnie jak w skrócie JPEG. Grupę tą stanowiło konsorcjum firm i naukowców, którego celem było ustalenie standardu pozwalającego odtwarzanie materiałów wideo na urządzeniach różnych marek (na przykład ta sama płyta DVD działała na dowolnym odtwarzaczu DVD). Pierwsza wersja wypracowanych przez konsorcjum standardów (zwana MPEG-1) miała trzy metody przechowywania ścieżki dźwiękowej (warstwy 1, 2 i 3). Jedna z tych metod (warstwa 3 MPEG-1) stała się bardzo popularna w kompresowaniu muzyki i jej nazwa została skrócona do MP3.
Standard MPEG-1 nie jest już obecnie używany w przypadku wideo (płyty DVD i telewizja używają głównie MPEG-2), ale jest bardzo ważny w przypadku kodowania audio.
Współczesną wersją MPEG jest MPEG-4 (MPEG-3 przedawnił się, zanim został uznany za standard). MPEG-4 oferuje wideo wyższej jakości i jest powszechnie stosowany do kodowania plików wideo, transmisji strumieniowych, dysków blu-ray i w przypadku niektórych programów telewizyjnych. Metoda kompresji audio AAC, używana między innymi przez Apple, również pochodzi ze standardu MPEG-4. Na komputerach, MPEG-4 part 14 jest powszechnie używany do wideo, a jego skrócona nazwa to MP4.
Podsumowując: MP3 oznacza „MPEG-1 layer 3”, natomiast MP4 jest skrótem od „MPEG-4 part 14”.
Pozostałe metody kompresji dźwięku wykorzystują podobne rozwiązania co algorytm MP3, i niektóre z nich oferują lepszą jakość przy podobnym rozmiarze pliku (lub mniejszy rozmiar przy tej samej jakości). Nie będziemy dokładnie prezentować zasad działania tych algorytmów, ale ogólna idea sprowadza się do rozłożenia dźwięku na pasma o różnych częstotliwościach, a następnie przedstawienie każdego z tych pasm jako sumy fal cosinusowych.
Na stronie CS4FN znajdziesz więcej informacji na temat mp3, jak również w artykule na tej stronie (po angielsku).
Inne dostępne systemy kompresji dźwięku to: AAC, ALAC, Ogg Vorbis i WMA. Każda z tych metod ma pewne zalety w stosunku do innych, niektóre są bardziej kompatybilne z urządzeniami lub nie wymagają licencji.
Jak mały może być plik? Jak czułe jest ludzkie ucho? Oto główne pytania dotyczące skompresowanego dźwięku. (Dodatkowo pojawia się pytanie, ile czasu zajmuje kodowanie pliku, co może być istotne dla praktyczności systemu). Kompromis między jakością a wielkością plików audio może zależeć od sytuacji, w której muzyka jest odtwarzana. Jeśli biegasz i słuchasz muzyki, jakość może nie mieć większego znaczenia, dzięki czemu można ograniczyć przestrzeń potrzebną do jej przechowywania. Z drugiej strony, jeśli słuchamy nagrań w domu na dobrym sprzęcie, jakość może odgrywać o wiele większą rolę niż rozmiaru plików.
Aby ocenić stopień kompresji pliku audio, należy przyjrzeć się oryginalnym nagraniom wysokiej jakości, takim jak płyta CD (lub nieskompresowane pliki WAV lub AIFF). Przygotuj pliki audio z różnymi stylami muzycznymi oraz innymi rodzajami dźwięku, takimi jak mowa lub nawet cisza. Przekowertuj te nagrania do różnych formatów audio. Jednym z narzędzi, które to umożliwia, jest iTunes firmy Apple. Można go użyć do zgrywania płyt CD i zapisu w różnych formatach, po uprzednim ustaleniu jakości i wielkości. Wiele innych programów audio oferuje podobne możliwości.
Skompresuj każde z przygotowanych nagrań przy użyciu różnych metod, po upewnieniu się, że każdy skompresowany plik jest tworzony z oryginału wysokiej jakości. Stwórz tabelę pokazującą, ile czasu zajęło przetwarzanie każdego nagrania, jaki jest rozmiar skompresowanego pliku oraz ocenę jakości dźwięku w porównaniu z oryginałem. Prześledź związki pomiędzy jakością a rozmiarem -- czy potrzebujesz dużo większych plików do przechowywania dobrej jakości dźwięku? Czy istnieje minimum dla rozmiaru pliku, który zachowuje akceptowalną jakość? Czy w przypadku mowy niektóre metody działają lepiej niż inne? Czy 2-minutowe nagranie ciszy zajmuje więcej miejsca niż 1 minuta nagrania ciszy? Czy 1 minuta muzyki zajmuje więcej miejsca niż minuta ciszy?
W rozdziale tym przedstawione zostały podstawowe informacje dotyczące kompresji, wiele szczegółów zostało jedynie wspomnianych. Sporo miejsca zostało poświęcone rozmiarom plików i szybkości algorytmów kompresji. Większość systemów kompresji to warianty pomysłów, które zostały tutaj omówione. Istnieje algorytm, o którym nie wspomnieliśmy, choć jest jednym z najważniejszych algorytmów kompresji. Chodzi o kodowanie Huffmana, które okazuje się przydatne jako ostatni etap wszystkich powyższych metod i często jest jednym z pierwszych tematów wymienionych w podręcznikach omawiających kompresję (krótkie wyjaśnienie (po ang.) tutaj). Nie wspomnieliśmy też o kodowaniu artymetycznym (krótkie wyjaśnienie (po ang.) tutaj). Kompresja wideo została również pominięta, mimo iż to właśnie ten typ kompresji daje największe oszczędności przestrzeni dyskowej. Większość metod kompresji wideo jest oparta na standardzie „MPEG” (ang. Moving Pictures Experts Group). Nieco więcej informacji na ten tamat zawiera artykuł CS4FN o „filmowej magii”.
-
Dla nauczyciela. Podręczniki dla nauczycieli z zasobów Plymouth
Dostęp do podręczników z zasobów Plymouth (odnośniki do nich są w poprzednim akapicie) są dotępne tu.
Zaprezentowana metoda Ziva-Lempela jest odmianą metody zwanej „LZ77”. Wiele algorytmów kompresji bezstratnej bazuje na tych metodach. Innym popularnym algorytmem o podobnym działaniu jest „LZW”. Inną efektywną metodą kompresji ogólnego przeznaczenia jest bzip, oparty na bardzo sprytnej metodzie zwanej transformacją Burrowsa-Wheelera.
Pytania typu „jaki jest najwyższy możliwy stopień kompresji” są przedmiotem badań teorii informacji. Na stronie CS Unplugged zamieszczone jest ćwiczenie poświęcone teorii informacji (po angielsku, ale zawierające polską instrukcję), a na stronie uniwersytetu W San Diego -- ćwiczenie interaktywne ilustrujące teorię informacji. Z tej teorii wynika, że tekst w języku angielskim nie może być skompresowany do mniej niż 12% oryginalnego rozmiaru. Zdjęcia, dźwięki i materiały wideo mogę być kompresowane z większą skutecznością, gdyż możemy stosować kompresję stratną.
- Książka The Data Compression Book Marka Nelsona i Jeana-Loupa Gailly (Press New York, 1995) zawiera solidne omówienie zagadnienia kompresji.
- Listę książek poruszających temat kompresji można znaleźć na stronie The Data Compression Site.
- Książka Jamesa Gleicka Informacja. Bit, wszechświat, rewolucja (Znak, 2012) jest dobrym podręcznikiem na temat kompresji i kodowania.
- obrazy, kodowanie długości serii na stronie CS Unplugged, z polską instrukcją;
- kompresja tekstu na stronie CS Unplugged, z polską instrukcją;
- Wikipedia (po angielsku) zawiera szczegółowy opis metody kodowania JPEG.