Grafika komputerowa kojarzy się z grami, filmami i obrazami oraz niezwykłym oprogramowaniem do tworzenia i przetwarzania obrazów. Warto jednak zapytać: Jak to się dzieje, że to oprogramowanie tak świetnie działa? Jaką rolę odgrywają informatycy? Oni nie są wyłącznie użytkownikami systemów graficznych, ale zajmują się tworzeniem, zwłaszcza obmyślaniem nowych technik.
Rozwój narzędzi do tworzenia grafiki komputerowej jest pochodną przemysłu rozrywkowego. Granice możliwości takiego oprogramowania nieustannie się poszerzają. Na początku były proste filmy animowane, zwane dziś 2D, a dziś na ekranach kin możemy oglądać postaci i obiekty w wersji 3D wygenerowane komputerowo, które momentami trudno odróżnych od tych istniejących w świecie rzeczywistym. Wśród napisów końcowych filmów, w których używano komputerowo wygenerowanych animacji, można by odnaleźć liczne nazwiska informatyków. Kilku z nich otrzymało nawet Oscary (Nagrody Akademii Filmowej)!
Firmy z braży filmowej czy producenci gier komputerowych nie ograniczają się do korzystania z istniejącego oprogrogramowania graficznego. Czasami niezbędni są informatycy, którzy tworzą nowe, lepsze algorytmy i oprogramowanie, dzięki którym uzyskuje się nowatorskie efekty. Możliwości rozwoju w tej dziedzinie wydają się nieskończone!
Grafika komputerowa znajduje zastosowanie w wielu różnych sytuacjach. Tworzenie gier i filmów animowanych to ważne przykłady, ale jest ich znacznie więcej: wizualizacja informacji zawartych w wielkich zbiorach danych (np. dotyczących połączeń telefonicznych w konkretnym dniu albo relacji znajomości użytkowników sieci społecznościowej), graficzna strona interfejsów komunikacji człowieka z komputerem, modelowanie tzw. rzeczywistości wirtualnej czy rozszerzonej oraz wiele innych.
-
Co to znaczy?. Piksele
Obraz cyfrowy wyświetlany na ekranie monitora lub wydrukowany na domowej drukarce jest skończonym zbiorem elementów, które łącznie tworzą jakby siatkę kwadratów bardzo małych rozmiarów, zwanych pikselami. Zazwyczaj nie da się ich dostrzec gołym okiem (inaczej obraz wyglądałby topornie). Na zdjęciach liczba pikseli jest liczona w milionach (megapiksel to milion pikseli; np. ekran o 1080 pikselach w poziomie i 720 w pionie składa się z 777 600 pikseli, czyli ok. 0,78 megepikseli).
Pojęcie piksela jest podstawowe w grafice komputerowej, praca programistów w dziedzinie grafiki komputerowej to w dużej części praca nad abstrakcyjnymi modelami obiektów graficznych złożonych z pikseli i algorytmami działajacymi na nich. Efektem działania aparatu cyfrowego jest zapisanie informacji o zarejestorwanych na elementach światłoczułych kolorach jako zbioru pikseli, które później będą wyświetlone na takim lub innym ekranie.
W tym rozdziale przyjrzymy się wybranym podstawowym technikom, które są używane w grafice komputerowej. Dzięki temu zorientujesz się z grubsza, z jakimi wyzwaniami mierzą się programiści grafiki.
W tym rozdziale będziemy używać systemu o nazwie WebGL, który służy do uzyskanie grafiki 3D w przeglądarce internetowej. Gdyby pojawił się problem z wydajnością lub inny, pomocne mogą być informacje zamieszczone tutaj.
Generowanie obrazów w grafice komputerowej wymaga wykonania wielu obliczeń matematycznych. Kolor każdego z pikseli tworzących obraz oglądany na monitorze jest ustalony w wyniku obliczeń, zwykle składających się z wielu etapów pośrednich.
Zaczniemy od kilku prostych, ale powszechnie stosowanych w programowaniu grafiki, przykładów obliczeń. Poniższa aplikacja pokazuje sześcian, który na trzech ze ścian ma coś napisane. Możesz poruszać sześcianem, używając przekształcenia, które po prostu ustala na nowo położenie sześcianu w przestrzeni. Wpisując współrzędne 3D, możesz oglądać ściany w poszukiwaniu symboli.
W tej zabawie stosowano przekształcenie zwane przesunięciem (translacją), co oznacza przemieszczenie obiektu w trzech wymiarach: w górę i w dół, do tyłu i do przodu oraz na boki.
Następne ćwiczenie wymaga obracania pudełkiem. Ponownie twoim zadaniem jest odnaleźć symbole na ściankach.
Różnych typów przekształceń jest wiele, ale najczęściej stosowane to przesunięcie (translacja), obrót i skalowanie (zmiana rozmiaru). Przekształcenia w grafice komputerowej dotyczą nie tylko obiektów tworzących obraz, ale również położenia tzw. kamery jak i źródeł oświetlenia.
W tym podrozdziale będziesz przekształcać obrazy. Zaczniemy od wprowadzenia zmian ręcznie, po jednym punkcie, ale potem przejdziemy do szybszej metody, która korzysta z matematycznego pojęcia macierzy. Na początek przyjrzymy się działaniu przekształcenia w dwóch wymiarach, by łatwiej było temat zrozumieć.
W aplikacji poniżej widzisz siedmiokąt tworzący jakby strzałkę, umieszczony w centralnej części układu współrzędnych, zwanego kartezjańskim. Po prawej stronie znajduje się m.in. lista par liczb (x,y), współrzędnych wierzchołków siedmiokąta (strzałki). Wartość x określa położenie punktu w poziomie (względem początku układu współrzędnych), a wartość y określa położenie punktu w pionie. Na przykład: pierwszy punkt na liście jest opisany parą liczb (0,2) i jest to punkt położony dwie jednostki powyżej punktu (0,0). Jakiemu punktowi odpowiada para liczb (2,0)? Co się dzieje, gdy wartość współrzędnej x jest liczbą ujemną?
-
Dla nauczyciela. Odpowiedzi
(2,0) to wierzochłek strzałki najbardziej wysunięty na prawo. Ujemna wartość x oznacza, że punkt położony jest po lewej stronie punktu (0,0). Podobnie ujemna wartość y oznacza, że punkt położony jest poniżej punktu (0,0).
Oprócz listy współrzędnych wierzchołków, widzisz jeszcze druga listę, jakby kopię tej pierwszej. Możesz ją edytować, tzn. wpisywać inne od początkowych wartości. W układzie współrzędnych zobaczysz efekt przekształcenia. Innymi kolorami zaznaczono postać początkową i tę po zmianach.
Uwaga: Możesz posługiwać się wyrażeniami arytmetycznymi zapisanymi tak: 2 * (2 + 1)'. Możesz też używać ułamków, zapisując je tak: '1/5'.
-
Dla nauczyciela. Rozwiązanie
Pierwsze przekształcenie w ćwiczeniu przesuwa strzałkę o dwie jednostki w prawo i trzy jednostki w górę. Drugie -- o trzy jednostki w dół i w lewo.
Przekształcenie zwane przesunięciem służy do zmiany położenia punktu (zbioru punktów) w układzie współrzędnych. Ten typ przekształceń jest używany w grafice komputerowej do określenia położenia obiektu, ale również do innych celów, np. animowania przesunięcia obiektu wzdłuż jakiejś ścieżki, czy określenia położenia kamery (punktu obserwacyjnego).
W następnym ćwiczeniu będziesz zmieniać rozmiar obrazu.
Sprawdź, jaki będzie efekt, gdy wartości docelowych współrzędnych x i y ustawisz jako podwojone wartości początkowych. Co się stanie, gdy podwoisz jedynie wartości dla współrzędnych x?
-
Dla nauczyciela. Rozwiązanie
Pomnożenie przez 2 skutkuje dwukrotnym powiększeniem strzałki w każdym z wymiarów. Pomnożenie przez 10 większa rozmiar 10 razy i obiekt nie zmieści się w polu widzenia. Pomnożenie przez 0,5 zmniejszy strzałkę dwukrotnie. Pomnożenie tylko watości x skutkuje wyłącznie zmianą strzałki w poziomie.
To przykształcenie nosi nazwę skalowania i służy do ustalania rozmiaru obiektu. Wykorzystane w odpowiedni sposób tworzy efekty takie jak przybliżanie obiektu lub jego oddalanie (od punktu obserwacyjnego).
W poniższej aplikacji nakładasz strzałki jedna na drugą. Należy zastosować zarówno operację skalowania, jak i przesunięcia.
Co się stanie, gdy zamienimy miejscami wartości x i y współrzędnych punktów?
Efekt wygląda jak obrót wokół punktu (0,0) o 90 stopni w prawo (zgodnie z ruchem wskazówek zegara). [Gdyby nasza figura nie była taka „regularna”, na przykład przypominała literę L, zauważyłbyś, że efekt obrotem nie jest (przyp. tłum.).] Takie przekształcenie może służyć również do symulacji zmiany ustawienia kamery (obserwatora).
Oczywiście ręczna zmiana wartości współrzędnych punktów, jednego po drugim, jest nieefektywna. Na szczęście jest na to sposób. O tym przeczytasz poniżej!
-
Dla nauczyciela. Wymagania co do wiedzy uczniów
Ten podrozdział jest wprowadzeniem do zastosowania macierzy w grafice komputerowej. Nie jest konieczne, aby uczniowie znali pojęcie macierzy wcześniej. Gdyby wyjaśnienia zawarte w tekście były niewystarczające do zrozumienia tematu przez uczniów, to można im wskazać inne zasoby edukacyjne, np. nagrania wideo i zadania pochodzące z Khan academy.
Oto inne odnośniki do materiałów edukacyjnych (w języku angielskim):
- Math is Fun -- Mnożenie macierzy
- Math in Sight -- Mnożenie macierzy
- Math Planet -- Przekształcenia z użyciem macierzy
- Wikipedia -- O przekształceniach macierzowych -- w tym artykule poziom szczegółowości jest już znaczący.
Istnieje o wiele prostszy sposób określenia paramatrów przekształcenia niż zmiana wartości współrzędnych punktów jednego po drugim. W grafice komputerowej używa się zwykle operacji na macierzach, które w istocie są skrótowym zapisem wykonania wielu prostych operacji arytmetycznych naraz. Macierz przekształceń dwuwymiarowych, które wykonaliśmy powyżej, składa się z czterech liczb. W konkretnym przypadku, gdy każdą ze współrzędnych mnożymy przez 2, macierz ma postać:
Aby lepiej to zrozumieć, uruchom poniższą aplikację:
(Na tym etapie czytania przewodnika warto pracować z dwoma oknami przeglądarki: w jednym czytasz tekst, a w drugim pracujesz z narzędziem.)
Zmień liczby w macierzy na takie:
lub
-
Dla nauczyciela. Wyjaśnienie
Efekty powinny być odpowiednio takie: strzałka powiększona trzy razy (w każdym z wymiarów) i strzałka pomniejszona do 1/5 wielkości (w każdym wymiarze).
Wartości wpisane do pola opisanego jako "add translate" są dodawane do współrzędnych x i y; sprawdź, jak to działa. Następnie postaraj się znaleźć takie wartości w tym polu (i w polu macierzy), aby w efekcie nałożyć strzałkę na strzałkę czerwoną.
-
Dla nauczyciela. Wyjaśnienie
Macierz powinna mieć postać \(\begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix}\), a współrzędne x i y odpowiednio 5 i 4 (rozmiar strzałki dwa razy powiększony i przesunięcie 5 w prawo i 4 w górę).
Co stanie się, gdy użyjesz takiej macierzy, jak poniżej?
-
Dla nauczyciela. Wyjaśnienie
Wartość x jest dwa razy większa, ale wartość y jest powiększona cztery razy, więc w efekcie strzałka jest powiększona w pionie dwa razy bardziej niż w poziomie.
Teraz sprawdź efekt dla macierzy:
Teraz strzałka leży na osi X.
Górny wiersz macierzy ma wpływ na zmianę współrzędnych x w taki sposób, że określa udział początkowych wartości x i y w wartości x po przekształceniu. W przykładzie:
Górny wiersz macierzy zawiera następującą informację: w skład wartości x wchodzi podwojona wartość początkowej wartości x, i nic więcej, bo wpływ y jest opisany w macierzy liczbą 0. Krótko mówiąc: wartość x zostaje podwojona. Drugi wiersz macierzy ma wpływ na wartość y: na nową wartość y nie ma wpływu wartość początkowa x (bo w macierzy jest 0), a tylko początkowa wartość y, którą należy pomnożyć przez 4.
W tym momencie jasny powinien być sens macierzy \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}\). Nowa wartość x jest równa początkowej wartości y i vice versa.
Interesująca jest sytuacja, w której przekształcenie opisane jest np. taką macierzą:
Efektem będzie pewien obrót w prawo. Teraz wartość x jest efektem jakby zmieszania 0,7 początkowych wartości x i y.
W ogólnym przypadku do zapisu macierzy obrotu obiektu o kąt \(\theta\) w lewo (przeciwnie do ruchu wskazówek zegara), należy użyć funkcji trygonometrycznych sinus i cosinus:
-
Dla nauczyciela. Wyjaśnienie
Jeśli uczniowie znają funkcji trygnometrycznych, można poprzestać na przedstawieniu koncepcji: kąt mierzymy w stopniach, a wartości funkcji sinus i cosinus przyjmują wartości między −1 i 1.
Poniżej znajduje się ćwiczenie interaktywne nr 6.
Uwaga: W aplikacji możesz wpisywać zarówno wyrażenia typu cos(60), aby obliczyć cosinus 60 stopni, jak i konkretne wartości, np. 0.7 (jako przybliżenie).
Jaką postać ma macierz obrotu o 360 stopni?
-
Dla nauczyciela. Wyjaśnienie
Dla kąta 360 stopni otrzymamy macierz \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\), ponieważ \(\cos(360)=1\) i \(\sin(360)=0\). Taką macierz nazywa się tożsamościową (identycznościową), gdyż przekształcenie nią opisane nie zmienia niczego w położeniu obiektu. Taka macierz opisuje każdy z obrotów o kąt wielokrotności 360 stopni (również 0 stopni).
Macierz dla skalowania w ogólnej postaci jest trochę prostsza niż dla obrotu; jeśli chcesz, aby współczynnik zmiany rozmiaru obiektu był opisany liczbą s, to macierz ma postać:
Przekształcenia, jakim jest przesunięcie (translacja) nie można opisać macierzą tego typu. Dlatego w aplikacji jest dodatkowe pole do określenia wartości x i y przesunięcia obiektu.
Wykonaj kolejne ćwiczenie: przesuń niebieską strzałkę tak, aby pokryła się z czerwoną.
-
Dla nauczyciela. Rozwiązanie
Przesunięcie x o 5, a y o 4 (5 w prawo i 4 w górę). Macierz skalowania ma postać: \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\)
Kolejne narzędzie umożliwia składanie dwóch przekształceń: przesunięcia i skalowania. Co nalezy zrobić, aby niebieska strzałka pokryła się z czerwoną?
-
Dla nauczyciela. Rozwiązanie
Macierz ma postać: \(\begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix}\) (podwojenie rozmiaru). Przesunięcie dla x to 4, a dla y to 3..
Kolejnośc składania przekształceń (przesunięcia i skalowania) ma znaczenie. Sprawdź to, wykonując kolejne ćwiczenie.
-
Dla nauczyciela. Rozwiązanie
Macierz ma postać: \(\begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix}\) (znów podwojenie rozmiaru). Tym razem wartości opisujące przesunięcie są dwa razy mniejsze niż potrzebujemy, ponieważ po przesunięciu będzie jeszcze skalowanie. Dlatego dla x należy wpisać 2,5 a dla y -- wpisać 2.
Moża było zauważyć, że wartości opisujące przekształcenia zależą od odległości obiektu od punktu o współrzędnych (0,0), zwanym początkiem układu współrzędnych. Jeżeli chcesz, by obiekt się powiększył, ale jego środek pozostał w miejscu, najwygodniej zacząć od przesunięcia obiektu tak, by jego środek znalazł się w punkcie (0,0), potem przeskalować obiekt, a na końcu przesunąć z powrotem.
-
Dla nauczyciela. Rozwiązanie
Wartości dla przesunięcia to: 8 dla x i −7 dla y. W efekcie wierzchołek strzałki leży w punkcie 0 i podwojenie rozmiaru nie zmieni położenia tego wierzchołka. Macierz ma postać: \(\begin{bmatrix} 2 & 0 \\ 0 & 2 \\ \end{bmatrix}\). Wartości dla przesunięcia strzałki z powrotem to: −8, 7.
Podobny problem pojawia się w przypadku obrotu. W poniżej aplikacji można poprzedzić skalowanie przesunięciem obiektu.
W kolejne dwóch przykładach można składać trzy rodzaje przekształceń: obroty, skalowania i przesunięcia. Możesz używać wielu macierzy, aby osiągnać cel: wynik działania jednej macierzy staje się danymi wejściowymi dla następnej. Przy okazji: szerokość strzałki jest podwojona, ale wysokość się zmieniła.
-
Dla nauczyciela. Rozwiązanie
Istnieją dwa rozwiązania, w zależności od wyboru pierwszego przekształcenia: skalowania lub obrotu. W pierwszym przypadku macierz skalowania ma postać: \(\begin{bmatrix} 2 & 0 \\ 0 & 1 \\ \end{bmatrix}\). Macierz obrotu to: \(\begin{bmatrix} 0 & 1 \\ -1 & 0 \\ \end{bmatrix}\). Wektor przesunięcia ma współrzedne 4, −2.
W drugim przypadku macierz obrotu ma postać: \(\begin{bmatrix} 0 & 1 \\ -1 & 0 \\ \end{bmatrix}\) (90 stopni zgodnie z ruchem wskazówek zegara), ale macierz skalowanie jest inna: \(\begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}\), gdyż skalowanie musi tym razem być w kierunku y. Wektor przesunięcia ma współrzedne 4, −2.
Istnieje też rozwiązanie z jedną macierzą (opisującą obrót i skalowanie); to może być ciekawe wyzwanie dla zainteresowanych. Macierz będzie mieć postać: \(\begin{bmatrix} 0 & 1 \\ 2 & 0 \\ \end{bmatrix}\). Wektor przesunięcia ma współrzedne 4, −2.
Oto jeszcze jedno ćwiczenie, grupujące wszystkie przekształcenia:
-
Dla nauczyciela. Rozwiązanie
Rozwiązań może być wiele. Najprostsze to: \(\begin{bmatrix} 0{,}7 & -0{,}7 \\ 0{,}7 & 0{,}7 \\ \end{bmatrix}\) jako (przybliżona) macierz obrotu, \(\begin{bmatrix} 0{,}5 & 0 \\ 0 & 0{,}5 \\ \end{bmatrix}\) jako macierz skalowania i −1, −2 jako wartości przesunięcia.
Może się wydawać, że stosowanie wielu przekształceń jest żmudne, bo każdy punkt należący do obiektu należy poddać przekształceniom. Strzałka z przykładu to był wielokąt o 7 wierzchołkach, a złożone obrazy składają się z tysięcy, czy nawet milionów punktów. Na szczęście operacje macierzowe można na początku złożyć w jedną operację i wykonać tylko tę jedną na każdym punkcie obiektu.
Jeśli obraz ma zostać poddany kilku przekształceniom jedno po drugim, to wówczas ten zbiór przekształceń należy opisać jedną macierzą, gdyż prowadzi to zmniejszenia liczby obliczeń. Taką macierz wypadkową uzyskuje się przez „wymnożenie” macierzy opisujących każde ze składowych przekształceń.
Wynikiem mnożenia dwóch macierzy nie jest macierz złożona z iloczynów wartości odpowiadająch sobie nawzajem elementów macierzy; poniżej przedstawiono przykład ilustrujący zasadę mnożenia dwóch macierzy:
To może wydawać się trochę skomplikowane, ale trud zrozumienia opłaca się w praktyce: otrzymujemy jedną macierz, która opisuje złożenie dwóch przekształceń.
Rozważmy prosty przykład. Chcemy złożyć dwa przekształcenia: skalowanie (zmiana rozmiaru) przez 2 i obrót o (prawie) 45 stopni. Jak będzie wyglądać macierz opisująca złożenie tych przekształceń?
Możesz sprawdzić działanie takiej macierzy, korzystając z aplikacji poniżej:
Warto sprawdzić inne przykłady, aby lepiej zrozumieć temat. Możesz posłużyć się narzędziem udostępnionym poniżej. Zwróć uwagę na to, że możesz tu zmieniać kolejność czynników (macierzy). Wystarczy przeciągnąć pola np. myszką.
Systemy grafiki komputerowej zwykle wymagają wykonania złożonych przekształceń, które można przedstawić jako matematyczne złożenie wielu prostych przekształceń. Obliczeń nie wykonuje się etapami (efekt działania poprzedniego przekształcenia stanowi dane do wykonania kolejnego przekształcenia). Projektanci systemu, do opisu przekształcenia złożonego, jeśli to tylko możliwe, używają jednej macierzy, która jest iloczynem macierzy opisujących składowe przekształcenia. Trzeba pamiętać, że złożone przekształcenie stosuje się czasem i dla miliona punktów naraz. Koszt znalezienia macierzy wypadkowej dla grupy przekształceń jest niewielki w porównaniu z kosztem obliczeń dla nieefektywnego rozwiązania.
Poniżej proponujemy projekt, który ma służyć pogłębieniu tego tematu. Podajemy tam odnośnik do interaktywnego narzędzia do ćwiczeń.
Do tej pory wykonywaliśmy tylko przekształcenia w dwóch wymiarach (na płaszczyźnie). Do opisu przekształceń w 3D potrzebujemy współrzędnej z, która opisuje trzeci wymiar, jakby głębość przestrzeni. Macierz dla operacji w 3D, gdzie każdy punkt ma przypisane trzy współrzędne, jest rozmiaru 3 na 3. Oto macierz opisująca podwojenie rozmiaru obiektu; każdą ze współrzędnych x, y i z mnożymy przez 2.
Poniżej narzędzie do ćwiczeń.
Obraz czajniczka składa się z 3644 punktów. Przekształcenie opisane macierzą jest wykonywane na każdym z nich.
Kolejne narzędzie umożliwia przesuwanie obiektu (z użyciem wektora). Zachęcamy do wykonania ćwiczeń.
Obrót jest trudniej opisać, gdyż w przestrzeni są trzy stopnie swobody. Na płaszczyźnie obroty wykonywane są wokół punktu (0,0), a w przestrzeni obroty wykonuje się wokół prostej (albo osi X, albo osi Y, albo osi Z, skierowanej jakby „w głąb” ekranu).
Do obracania w trzech kierunkach używa się takiej macierzy:
Spróbuj zastosować tę macierz do obrazu z ćwiczenia interaktywnego. Ta macierz stanowi opis obrotu wokół osi Z (prostej skierowanej „w głąb” ekranu); w istocie ten przykład to obrót w płaszczyźnie. Ostatni wiersz macierzy (0, 0, 1) pozostawia wartość bez zmian.
Poniżej znajduje się macierz opisującą obrót wokół osi X (współrzędna x pozostaje bez zmian: w pierwszym wierszu macierzy jest 1, 0, 0):
A poniżej macierz dla obrotu wokół osi y:
Poniższa aplikacja umożliwia składanie macierzy dla przekształceń 3D.
W tych przykładach, gdy dla pojedynczego punktu nalezałoby użyć kilku macierzy kolejnych przekształceń, można zaoszczędzić dużo czasu przez zastąpienie kilku macierzy jedną, która opisuje złożenie tych przekształceń. Poniżej znajdziesz narzędzie do ćwiczeń.
Na przykład, zapisz macierz skalowania razy 2, zmieniając 1 na przekątnej na 2, a następnie inną macierz, skalowania razy 3 (na przekątnej liczby 3). Po prawej stronie zobaczysz macierz, będącą opisem złożenia tych dwóch przekształceń. Co można zauważyć?
-
Dla nauczyciela. Wyjaśnienie
Efekt złożenia przekształceń skalowania razy 2 i razy 3 jest identyczny z efektem skalowania razy 6.
Narzędzie umożliwia też dodanie przekształcenia, jakim jest przesunięcie. Sprawdź, jak działa składanie skalowania i przesunięcia. Co będzie, jeśli dodasz obrót -- czy kolejność przekształceń ma znaczenie?
-
Ciekawostka. Mnożenie macierzy w 3D
Ktoś może być ciekaw, jak powstała macierz przekształcenia wypadkowego. Jest ona wynikiem mnożenia macierzy. Sposób, w jaki mnoży się macierze, jest opisany poniżej. Wydaje się skomplikowany, ale takie mnożenie jest bardzo użyteczne w grafice komputerowej, ponieważ dzięki niemu wiele kolejno wykonywanych przekształceń można opisać jedną macierzą, która jest stosowania dla każdego punktu obiektu. To redukuje w znaczący sposób liczbę obliczeń.
\[ \begin{aligned} &\begin{bmatrix} a_{11} & a_{21} & a_{31}\\ a_{12} & a_{22} & a_{32}\\ a_{13} & a_{23} & a_{33}\\ \end{bmatrix} \cdot \begin{bmatrix} b_{11} & b_{21} & b_{31}\\ b_{12} & b_{22} & b_{32}\\ b_{13} & b_{23} & b_{33}\\ \end{bmatrix} =\\ =&\begin{bmatrix} a_{11}b_{11}+a_{21}b_{12}+a_{31}b_{13} & a_{11}b_{21}+a_{21}b_{22}+a_{31}b_{23} & a_{11}b_{31}+a_{21}b_{32}+a_{31}b_{33}\\ a_{12}b_{11}+a_{22}b_{12}+a_{32}b_{13} & a_{12}b_{21}+a_{22}b_{22}+a_{32}b_{23} & a_{12}b_{31}+a_{22}b_{32}+a_{32}b_{33} \\ a_{13}b_{11}+a_{23}b_{12}+a_{33}b_{13} & a_{13}b_{21}+a_{23}b_{22}+a_{33}b_{23}& a_{13}b_{31}+a_{23}b_{32}+a_{33}b_{33} \\ \end{bmatrix} \end{aligned} \]
-
Projekt. Przekształcenia 3D
A teraz proponujemy wykonanie projektu, podsumowującego dotychczasowe ćwiczenia. Zadanie będzie polegać na zaprezentowaniu i opisie przekształceń 3D kilku obiektów. Należy pamiętać o wykonaniu zrzutów ekranu po każdym kroku, bo w aplikacjach, których będziesz używał, nie można zapisać grafiki.
Poniższe narzędzie umożliwia wybór obiektów (i ich kolorów etc.) i zastosowanie jednego z przekształceń. Wyzwaniem będzie zastosowanie całej serii przekształceń (np. skalowanie, potem obrót, a następnie przesunięcie) i w końcu znalezienie „uproszczenia” w postaci jednego wypadkowego przekształcenia.
To narzędzie pomoże znaleźć przekształcenie wypadkowe:
Prezentację wyników swojej pracy poprzedź przykładami obrazów 3D, na przykład pochodzących z filmów nagrodzonych za grafikę. Opowiedz, co w nich innowacyjnego.
Aby wykazać się rozumieniem podstaw grafiki komputerowej, zaplanuj rozmieszczenie kilku obiektów na obrazku (np. czajniczek obok kilku filiżanek) i spróbuj je odzwierciedlić w narzędziu interaktywnym. Wyjaśnij istotę zastosowanych przekształceń, pokazując macierze opisujące przekształcenia.
Podaj proste przykłady różnych przekształceń, również złożenia kilku przekształceń.
Pokaż, jak macierze składowe można zastąpić jedną macierzą wypadkową i objaśnij, używając konkretnych ilustracji, na czym polega efektywność tego rozwiązania.
-
Projekt. WebGL i OpenGL
Biegli w programowaniu, chcący zgłębiać temat przekształceń graficznych w praktyce, mogą wykonać projekt używając jednego z systemów programowania grafiki: WebGL (użyty do przygotowania narzędzi wyżej udostępnionych) lub powszechnie stosowany system OpenGL. Interaktywny samouczek (po angielsku) OpenGL można znaleźć tutaj: JPOT.
Wykonanie projektu w jednym z tych systemów może być bardzo czasochłonne. Trzeba się wiele nauczyć, zanim uda się uzyskać ciekawe efekty.
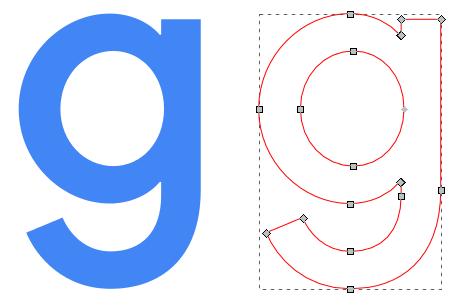
Podstawową operacją w grafice komputerowej jest rysowanie odcinków i okręgów. Na przykład kształt czcionki na ekranie jest opisany m.in. przez odcinki i łuki okręgów. Litera g jest zbiorem odcinków i fragmentów krzywych. Gdy wyświetlamy ją w powiększeniu na ekranie, wtedy kształt litery jest rysowany od nowa. Możemy ją powiększać bez obawy o utratę jakości, gdyż obraz litery nie jest skończonym zbiorem pikseli, nie ma stałej rozdzielczości rozdzielczości, a jest tzw. grafiką wektorową.
W przypadku grafiki 3D kształty obiektow są często zbiorem ocinkow i krzywych, które stanowią krawędzie małych płaskich powierzchni (zwykle trójkątów), zwykle niedostrzegalnych dla oka.
Odcinki i okręgi, które są składowymi obiektów, są zwykle w pamięci komputera zapisane jako liczby (np. dla odcinka zapisuje się punkty będące jego końcami, dla okręgu -- jego środek i promień). Program graficzny musi na tej podstawie określić piksele, które będą reprezentować odcinki i okręgi na ekraniu monitora. Czasem program musi określić położenie odcinka bez rysowania go.
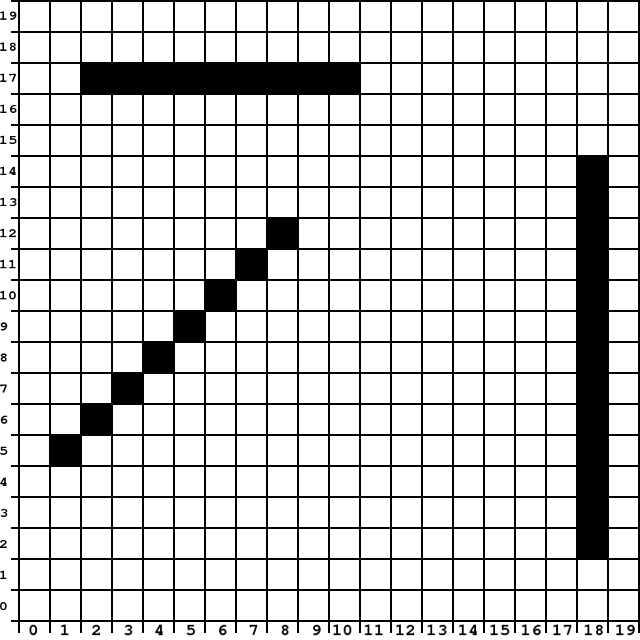
Poniżej widzisz powiększoną siatkę pikseli binarnego obrazu, na której znajduje się 5 odcinków. Wiersze i kolumny są ponumerowane. Odcinek pionowy ma początek w punkcie (2,9) i koniec w punkcie (2,16). Oczywiście taka grafika przedstawia tylko mały fragment ekranu. Monitory komputerowe wyświetlają zwykle ponad 1000 pikseli, zarówno w poziomie, jak i w pionie. Również na ekranach smarfonów odcinki składają się z setek pikseli.
Na papierze, używając linijki i cyrkla, można łatwo rysować figury geometryczne. Wyświetlenie takiej figury na ekranie komputera wymaga wykonania obliczeń dla wyznaczenia współrzędnych każdego z pikseli tworzących obraz figury. Wybór kiepskiej metody do wykonania takich obliczeń wpłynie na czas potrzebny na wyświetlenie zbioru pikseli i będzie miał fatalne skutki np. w przypadku animacji.
W tym podrozdziale przyjrzymy się bardzo prostym, ale sprytnym algorytmom, dzięki którym komputer szybko wykonuje niezbędne obliczenia.
-
Dla nauczyciela. Materiały dla uczniów
Do wykonania ćwiczeń uczniowie będą potrzebować kartek z wydrukowaną siatką kwadratową lub zwykłych kartek ze szkolnego zeszytu w kratkę.
Aby narysować odcinek, komputer musi wybrać piksele tak, aby ich zbiór wyglądał jak fragment linii prostej. Warto wykonać kilka prób samodzielnie, na papierze w kratkę (oczywiście kratki są wielokrotnie większych rozmiarów niż piksel na monitorze czy kropka na wydruku). Wybrany zbiór pikseli będziemy określać za pomocą dwóch wartości (x,y), gdzie x to odległość od lewego brzegu kartki, a y to odległość od dolnego brzegu kartki. Piksel w lewym dolnym rogu ma współrzędne (0,0), a piksel w prawym górnym roku ma współrzędną (19,19).
Na siatce kwadratowej 19 x 19 spróbuj narysować odcinki (jako zbiory zamalowanych kwadratów) łączące punkty:
- (2, 17) i (10, 17)
- (18, 2) i (18, 14)
- (1, 5) i (8, 12)
-
Dla nauczyciela. Rozwiązanie
Rysowanie linii równoległych do krawędzi ekranu lub leżących na głównej przekątnej ekranu jest łatwe; z narysowaniem odcinków, które tworzą z krawędzią ekranu inne kąty jest trudniej, gdyż trzeba wykonać odpowiednie obliczenia.
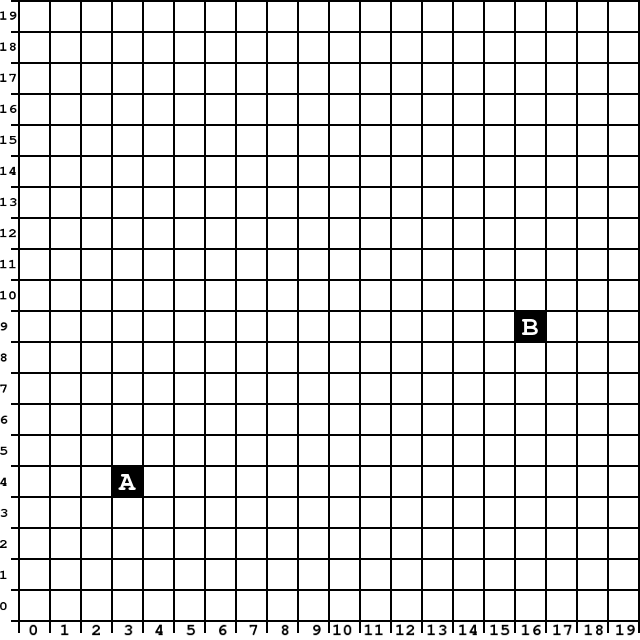
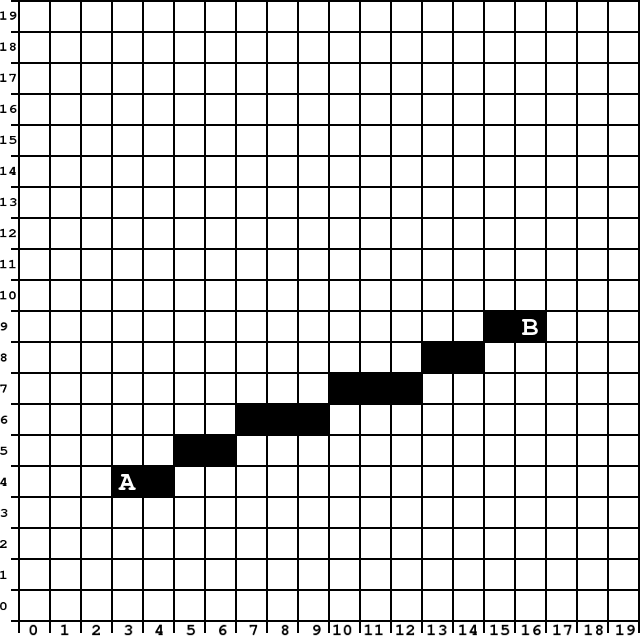
Potrafisz, bez użycia linijki, wybrać i zamalować odpowiednie pliksele tak, aby tworzyły odcinek z A do B? Spróbuj.
Sprawdź efekt, przykładając linijkę do rysunku. Umieść ją tak, aby krawędź linijki przechodziła przez środki małych kwadratów A i B. Czy linijka przechodzi przez wszystkie zamalowane piksele?
Prostą w układzie współrzędnych XY można opisać równaniem y = mx + c. Używając tego równania, możemy wyznaczyć wartość współrzędnej y dla wartości współrzednej x. Wcześniej trzeba określić wartość współczynnika opisującego nachylenie prostej, którym jest m oraz punkt, w którym prosta przecina oś Y, czyli (0, y). Współrzędna y tego punktu w równaniu jest oznaczona jako c. Innymi słowy, rysując linię prostą, wybieramy piksele o współrzędnych (x, mx + c) dla kolejnych wartości x.
Na przykład, wybierając m = 2 i c = 3 otrzymujemy prostą przechodzącą przez punkty (0,3), (1,5), (2,7), (3,9) itd. Zauważ, że dla kolejnych punktów współrzędne x rosną o 1, a współrzędne y rosną o 2 (bo m = 2). Pierwszy piksel jest położony 3 jednostki powyżej brzegu siatki (bo c = 3).
Poćwicz na innych przykładach, dla różnych wartości m i c (na przykład zacznij od c = 0 i sprawdź trzy przypadki m: m = 1, m = 0,5 i m = 0). Jakie są kąty nachylenia prostych?
-
Dla nauczyciela. Rozwiązanie
Wartość m = 0 odpowiada prostej równoległej do dolnej krawędzi, wartość m = 1 to przypadek prostej o kącie nachylenia 45 stopni (przesunięciu o 1 piksel w poziomie odpowiada przesunięcie o jeden piksel w pionie). Wartość m = 0,5 opisuje prostą o kącie nachylenia mniejszym niż 27 stopni. Artykuł Slope of a Line (ang.) może być pomocny w zrozumieniu związku wartości m z kątem nachylenia.
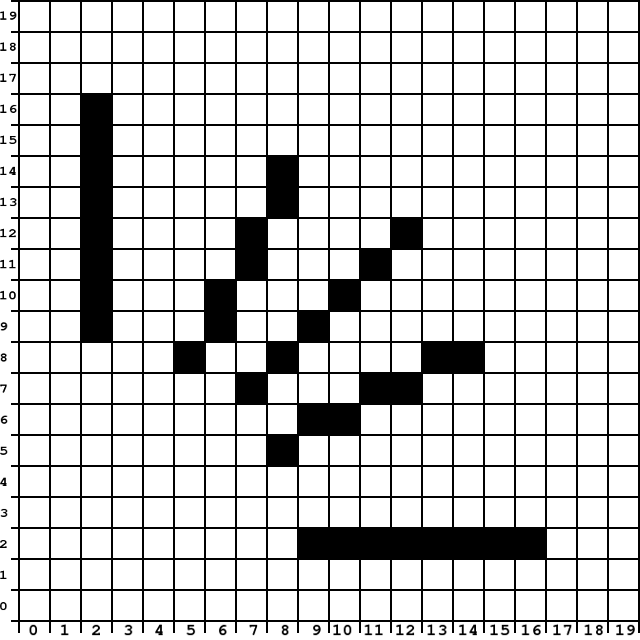
Równanie mx + c może być użyte do wybrania pikseli dla cyfrowej reprezentacji odcinka łączącego punkty \((x_1, y_1)\) i \((x_2, y_2)\). Jakie wartości mają współrzędne \((x_1, y_1)\) i \((x_2, y_2)\) w przykładzie poniżej?
-
Dla nauczyciela. Rozwiązanie
Końce odcinka to punkty: \(A = (3,4)\) i \(B = (16,9)\). To znaczy, że \(x_1 = 3, y_1 = 4, x_2=16\) i \(y_2 = 9\).
Potrafisz wyznaczyć wartości m i b dla równania prostej przechodzącej przez punkty A i B? Możesz użyć następujących wzorów:
-
Dla nauczyciela. Rozwiązanie
Oto wyniki obliczeń:
\[ m = \frac{(9 - 4)}{(16 - 3)} = 5/13 \approx 0,384615\\ b = \frac{(4 \cdot 16 - 9 \cdot 3)}{(16-3)} = 37/13 \approx 2,846154 \]Równanie ma więc postać \(y \approx 0.384615x + 2.846154\).
W kolejnym ćwiczeniu warto użyć arkusza kalkulacyjnego do określenia wartości y.
x y 3 4,000 4 4,385 5 4,769 6 5,154 7 5,538 8 5,923 9 6,308 10 6,692 11 7,077 12 7,462 13 7,846 14 8,231 15 8,615 16 9,000
Aby narysować odcien między punktami A i B (z poprzedniego ćwiczenia) wykonaj obliczenia, używając równania y = mx + c. Wyznacz odpowiednie wartości y dla kolejnych wartości x z zakresu od \(x_1\) do \(x_2\). Dla wskazania (jakby zapalenia na ekranie) odpowiednich pikseli, wartości y trzeba będzie zaokrąglić do najbliższej liczby całkowitej. Wartości y powinny być liczbami pomiędzy \(y_1\) i \(y_2\).
Po wykonaniu ćwiczenia sprawdź linijką, czy wynik jest lepszy od tego z pierwszej próby.
Zastanów się nad tym, ile obliczeń było niezbędnych do wyznaczenia każdego punktu (i wyboru piksela). Może wydawać się, że niewiele. Pamiętaj jednak, że obliczenia mogą w praktyce dotyczyć tysięcy odcinków składających się z setek punktów.
Okazuje się, że rozwiązanie wykorzystujące opisane wyżej równanie nie jest zbyt szybkie i w praktyce może być nieprzydatne (np. dla animacji i w grach komputerowych). W praktyce korzysta się ze znacznie bardziej efektywnej metody.
-
Dla nauczyciela. Rozwiązanie
Wyznaczenie każdego punktu wymaga wykonania mnożenia, dodwawania i także operacji zaokrąglania. Operacja mnożenia jest obliczeniowo dość kosztowną operacją (zwłaszcza gdy obraz składa się z tysięcy czy nawet milionów pikseli!). Co gorsza, metoda opisana wyżej wymaga wykonywania obliczeń w tzw. arytmetyce zmiennopozycyjnej, co jest o wiele bardziej czasochłonne niż operacje wykonywane na liczbach całkowitych.
Szybszym sposobem na wyznaczenie współrzędnych punktów tworzących odcinek na ekranie jest algorytm zaproponowany przez Jacka Bresenhama. Składa się z kilku etapów. Najpierw wyznacza się trzy wartości:
Oto kolejne kroki algorytmu.
- Zapal piksel początkowy.
Następnie dopóki nie napotkasz punktu końcowego, dla kolejnych wartości x, poruszając się wzdłuż osi X wykonuj:
- Jeśli \(P<0\), to zapal piksel położony bezpośrednio po prawej stronie wcześniej zapalonego i dodaj \(A\) do \(P\).
- W przeciwnym przypadku zapal piksel po prawej, położony wiersz wyżej niż wcześniej wybrany i dodaj \(B\) do \(P\).
Sprawdź działanie algorytmu Bresenhama, rysując ponownie odcinek z \(A\) do \(B\):
Sprawdź efekt przy pomocy linijki. Jak wyszło w porównaniu do wcześniejszych prób?
-
Dla nauczyciela. Rozwiązanie
Poniżej zapisano obliczenia wykonane z użyciem algorytmu Bresenhama:
Etap obliczeń Wybór piksela \(A = 10, B = -16\) Zapalenie piksela początkowego. \(P_0 = -3\) Kolejny zapalony piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_1 = 7\) Kolejny piksel to piksel po prawej w wierszu wyżej. \(P_2 = -9\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_3 = 1\) Kolejny piksel to piksel po prawej w wierszu wyżej. \(P_4 = -15\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_5 = -5\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_6 = 5\) Kolejny piksel to piksel po prawej w wierszu wyżej. \(P_7 = -11\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_8 = -1\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_9 = 9\) Kolejny piksel to piksel po prawej w wierszu wyżej. \(P_{10} = -7\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego. \(P_{11} = 3\) Kolejny piksel to piksel po prawej w wierszu wyżej. \(P_{12} = -13\) Kolejny piksel jest bezpośrednio po prawej stronie poprzedniego.
Przedstawiona powyżej wersja algorytmu Bresenhama była wersją niepełną, gdyż działała poprawnie tylko dla odcinków nachylonych do poziomu o kąt między 0 a 45 stopni (co odpowiada wartościom współczynnika nachylenia m od 0 do 1). Aby algorytm był uniwersalny, trzeba listę kroków algorytmu uzupełnić:
- W przypadku, gdy odcinek jest nachylony nie w górę, ale w dół, wówczas, gdy \(P \geq 0\), jako kolejny piksel należy zapalić ten położony po prawej w wierszu niżej.
- Jeśli wartość \(y\) rośnie szybciej niż wartość \(x\) (co odpowiada kątowi nachylenia większemu niż 45 stopni), to podczas obliczania wartości \(A\), \(B\) i początkowej wartości \(P\), zamień w algorytmie rolę osi X i Y rolami. Oznacza to, że zamiast poruszać się wzdłuż osi X, poruszasz się wzdłuż Y, a zamiast zapalać po jednym pikselu w każdej kolumnie, zapalasz po jednym pikselu w każdym wierszu.
Zaznacz na siatce kwadratowej dowolne dwa punkty. Wybierz je tak, aby nie łączył ich odcinek poziomy, pionowy, ani po przekątnej!
Użyj algorytmu Bresenhama do narysowania odcinka. Sprawdź, że w efekcie otrzymujesz te same piksele, które uzyskać można z użyciem linijki lub równania prostej y = mx + b. Ile operacji arytmetycznych (mnożenia i dodawania) było wykonanych przy wyznaczaniu zbioru pikseli metodą Bresenhama? Ile byłoby ich w przypadku posługiwania się równaniem y = mx + b? Który sposób jest szybszy? (Pamiętaj, że w większości przypadków koszt dodawania jest o wiele mniejszy niż koszt mnożenia.)
-
Dla nauczyciela. Szybkość metody Bresenhama
Ta metoda dla wskazania kolejnego piksela wymaga wyłącznie porównania jednej liczby całkowitej z zerem i jednego dodawania. Jest o wiele szybsza od metody z równaniem.
Możesz napisać program komputerowy lub użyć narzędzi arkusza kalkulacyjnego do wykonania obliczeń i narysowania odcinka -- tego wymaga się od programistów zajmujących się grafiką komputerową.
Oprócz odcinków prostej, często komputery muszą rysować okręgi. Algorytm Bresenhama rysowania odcinków przystosowano do rysowania okręgów.
Dany okrąg jest jednoznacznie określony przez jego środek i promień. Przypomnijmy, że okrąg jest zbiorem punków oddalonych o promień od środka.
Spróbuj narysować okrąg „na oko”, bez posługiwania się cyrklem. Dlaczego nie jest to takie proste?
Do określenia pikseli tworzących rysunek okręgu można by użyć twierdzenia Pitagorasa, ale to wymagałoby wielokrotnego obliczania pierwiastka kwadratowego, a tego nie da się zrobić zbyt szybko. Poniżej opisany algorytm jest o wiele szybszy. Poza tym posługuje się wyłącznie prostymi operacjami arytmetycznymi.
Oto kolejne kroki algorytmu dla okręgu o środku (\(c_{x}\), \(c_{y}\)) i promieniu \(R\):
Powtarzaj kolejne kroki aż \(y\) będzie mieć większą wartość niż \(x\):
- Zapal piksel o współrzędnych (\(c_{x} + x\), \(c_{y} + y\)).
- Zwiększ \(E\) o wartość wyrażenia \(2 \cdot y + 1\).
- Zwiększ \(y\) o 1.
- Jeśli \(E \geq 0\), to odejmij wartość \(2 \cdot x - 1\) od \(E\), a następnie odejmij 1 od \(x\).
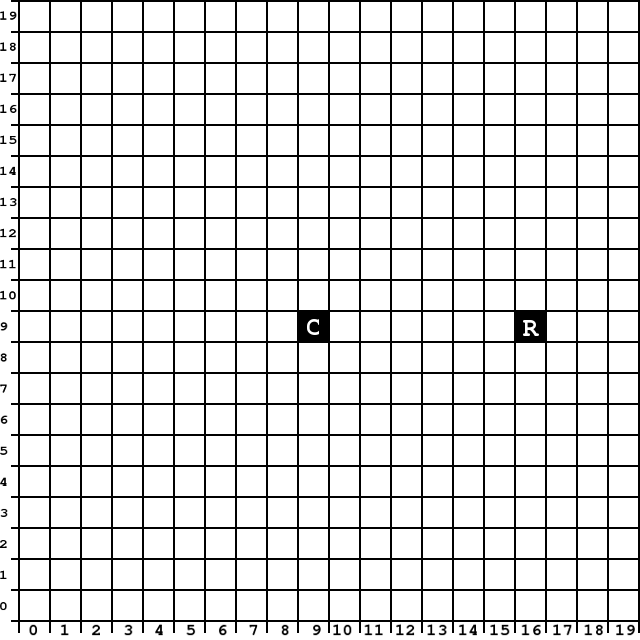
Zastosuj algorytm, by stworzyć rysunek okręgu na siatce kwadratowej. Piksel opisany literą \(C\), o współrzędnych (\(c_{x}\), \(c_{y}\)) niech będzie środkiem okręgu, a piksel \(R\) -- jednym z punktów na okręgu. Zwróć uwagę na to, że zgodnie z algorytmem rysowanie należy przerwać, gdy \(y\) będzie większe niż \(x\).
-
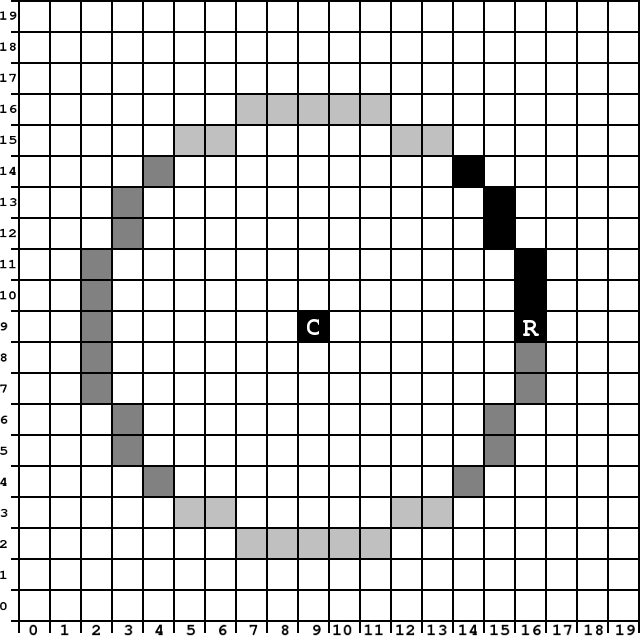
Dla nauczyciela. Rozwiązanie
Na rysunku poniżej zaczerniono piksele uzyskane po wykonaniu algorytmu (jest to ośma część okręgu). Ciemnym szarym kolorem zaznaczono piksele uzyskane kolejno jako efekt symetrii osiowych (odbić lustrzanych) względem prostych równoległych do osi X i osi Y. Jasnym szarym kolorem zaznaczono piksele, które są obrazem pikseli w symetrii względem przekątnej siatki. Warto, aby uczniowie samodzielnie poszukali odpowiednich przekształceń. (Dla symetrii względem przekątnych osiami symetrii są proste o współczynnikach kierunkowych 1 i −1.)
Oto etapy obliczeń:
Etap obliczń Wybrany piksel \(E_0 = -7, X_0 = 7, Y_0 = 0\) Zapalenie piksela (16, 9) \(E_1 = -6, Y_1 = 1\) Zapalenie piksela (16, 10) \(E_2 = -3, Y_2 = 2\) Zapalenie piksela (16, 11) \(E_3 = 2, Y_3 = 3\) - \(E_4 = -11, X_4 = 6\) Zapalenie (15, 12) \(E_5 = -4, Y_5 = 4\) Zapalenie (15, 13) \(E_6 = 5, Y_6 = 5\) - \(E_7 = -6, X_7 = 5\) Zapalenie (14, 14) \(E_8 = 5, Y_8 = 6\) y > x, co oznacza, że mamy ośmą część okręgu narysowaną
-
Co to jest?. Kwadranty i oktanty
Kwadrant to ćwiartka jakiegoś obszaru. Oktant to ośma część jakiegoś obszaru.
W istocie komputer nie wykonuje wielu dodatkowych obliczeń w celu narysowania 7/8 okręgu. Algorytm wyznacza w każdej iteracji dwie liczby \((x, y)\), które określają położenie piksela względem środka okręgu. Z łatwością wówczas wskazać 7 par liczb odpowiadających \((x, y)\) w odpowiedniej symetrii:\((x, -y)\), \((-x, y)\), \((-x, -y)\), \((y, x)\), \((y, -x)\), \((-y, x)\) i \((-y, -x)\). W sumie mamy 8 pikseli w każdej iteracji.
Warto dodać, że algorytm można dostosować do rysowania elips. Wówczas bazą dla rysunku jest 1/4 elipsy.
Komputery rysują odcinki prostych, okręgi i elipsy na potrzeby różnych zastosowań praktycznych: grafiki w grach komputerowych, grafiki w programach dla architektów etc. Nawet kropka nad „i” w dokumencie tekstowym musi być narysowana jako okrąg, gdy jest wyświetlana na ekranie. Przez wzbogacenie metod rysowania odcinków i okręgów różnymi technikami wypełniania krzywych i wygładzania, można uzyskać efektowne gładkie krawędzie obiektów wyświetlanych na ekranie. W przypadku takich grafik nie ma ograniczenia rozdzielczości.
Taką grafikę nazywa się grafiką wektorową. Ma tę własność, że podczas powiększania rysunku unikniemy efektu pikselizacji. Powiększanie oznacza zwiększenie szczęgółowości obrazu, więc element obrazu jest rysowany wówczas na nowo, liczba pikseli tworzących obraz jest dopasowywana do rozmiaru ekranu. Koszt to obliczenia, które trzeba wykonać. Dlatego używa się szybkich algorytmów.
Najbardziej powszechne rysunki wektorowe to rysunki konturów czcionek wyświetlanych na ekranie.
Informatycy zajmują się projektowaniem szybkich algorytmów dla grafiki komputerowej. Nie chodzi tu wyłącznie o szybkość wyświetlania. Dzięki postępowi w tej dziedzinie oszczędza się również na żywotności np. baterii smartfonów, gdyż nie obarcza się ich procesorów zbędnymi obliczeniami.
Jak zwykle, szczegóły są bardziej złożone. Na przykład, wyobraźmy sobie odcinek łączący punkty (0,0) i (10,0), złożony z 11 pikseli. Następnie porównajmy go z odcinkiem pochylonym pod kątem 45 stopni, łączącym punkty (0,0) i (10,10). Jego rysunek składa się z 11 pikseli, ale odcinek jest dłuższy (o ok. 41%).
Jako skutek uboczny otrzymujemy więc różnej grubości odcinki na ekranie. Tak postrzega je nasze oko. Aby zredukować to wrażenie, stosuje się różne techniki, przede wszystkim wygładzanie (ang. anty-aliasing).
-
Projekt. Algorytmy rysowania odcinka
Porównaj dwie metody rysowania odcinka: tę korzystającą ze wzoru y = mx + b oraz algorytm Bresenhama.
Wybierz punkt początkowy odcinka i punkt końcowy odcinka. Zapisz obliczenia, które pozwolą ustalić współrzedne pozostałych punktów odcinka na siatce. Zlicz operacje dodawania, odejmowania, mnożenia i dzielenia w każdym z przypadków.
Operacje dodawania i odejmowania są dla komputera o wiele mniej kosztowne niż operacje mnożenia i dzielenia. Koszt operacji możesz oszacować, pisząc program, który zmierzy czas wykonania tysięcy takich operacji. Na podstawie tych informacji oblicz, ile takich operacji na sekundę wykonuje komputer.
Zamiast porównywać efektywność metod rysowania odcinków, możesz to zrobić dla metod rysowania okręgów. Metoda nieefektywna będzie korzystać z twierdzenia Pitagorasa.
Powyżej ukazany jest tylko mały wycinek dziedziny, jaką jest grafika komputerowa. Informatycy projektują algorytmy dla wielu obszarów grafiki komputerowej:
- oświetlenia (np. w celu uzyskania efektu cienia w scenie 3D),
- teksturowania (np. w celu uzyskania możliwie realistycznego obrazu trawy, skóry, wody, drewana itd.),
- wygładzania (np. w celu zredukowania efektu ostrych krawędzi na obrazie),
- rzutowania (np. w celu odwzorowania obiektów 3D na płaszczyźnie),
- ukrywania obiektów (np. w celu określenia fragmentów obiektu niwidocznych dla obserwatora),
- renderowania fotorealistycznego (przy tworzeniu obrazów, które wyglądają jak obrazy pochodzące z rzeczywistości), jak i renderowania nierealistycznego, taki jak „renderowanie malarskie” (np. w celu uzyskania obrazu na wzór obrazów malarskich, czyli efektu pociągnienia pędzlem),
- symulowania zajwisk takich jak ogień, fale morskie, ruch człowieka itd.
System oparty na mnożeniu macierzy 3 x 3, przedstawiony w tym rozdziale to uproszczona wersja jednego z systemów, który oparty jest o współrzedne jednorodne. Używa się w nim macierzy 4 x 4. Jego zaletą jest to, że wszystkie operacje można realizować wyłącznie przez mnożenie (również przesunięcie). Upraszcza też inne operacje graficzne. Współczesne karty graficzne sprzętowo, a więc bardzo szybko, realizują operacje na współrzędnych jednorodnych.
-
Ciekawostka. Möbius i jego odkrycia
System współrzędnych jednorodnych wprowadził w 1827 roku niemiecki matematyk August Ferdinand Möbius, ponad 100 lat przed erą komputerów. Möbius jest prawodopoodbnie bardziej znany jako odkrywca pewnej matematycznej powierzchni jednostronnej, określanej jako wstęga Möbiusa!
Poniższe materiały są po angielsku.
- Wikipedia -- grafika komputerowa;
- Wikipedia -- macierz przekształcenia;
- Wikipedia -- algorytm Bresenhama;
- Wikipedia -- genrowanie obrazów metodą śledzenia promieni;
- o programie POV-Ray.