2. Algorytmy

Oprogramowanie urządzeń komputerowych, nawet prostego kalkulatora szkolnego jest zapisem odpowiedniego algorytmu. To pojęcie jest bardzo ważnym pojęciem w informatyce. Trudno wyobrazić sobie tworzenie sprawnego, efektywnego i bezbłędnie działającego oprogramowania bez korzystania z algorytmów. Już na początku trzeba podkreślić, że może być wiele algorytmów rozwiązujących dany problem, ale niektóre są o wiele lepsze od pozostałych!

Kliknij obrazek by rozpocząć sortowanie

Sortowanie przez wybór

Sortowanie metodą Quicksort

Animations provided by David Martin from www.sorting-algorithms.com

Komputery z niesamowitą szybkością przetwarzają informacje. Okazuje się, że ich moc może okazać się jednak niewystarczająca, jeśli chcielibyśmy ogromne zbiory danych przetwarzać (choćby przeszukiwać) w sposób mało przemyślany. Czas reakcji komputera na zadanie czy pytanie użytkownika nie może być zbyt długi. To byłoby frustrujące, niezależnie od tego, jak atrakcyjna jest szata graficzna programu. Z pewnością firmy takie jak Google, Facebook czy Twitter nie mogłyby sobie na to pozwolić! Dlatego od informatyków oczekuje się pomysłów na efektywne algorytmy, które w rozsądnym czasie poradzą sobie w przetwarzaniem nawet ogromnych zbiorów danych.

Oto rada pochodząca od Ralfa Gomory'ego, kiedyś szefa działu badawczego w IBM:

Jedynym sposobem przyspieszania komputerów jest obarczanie ich mniejszą liczbą działań.

Być może ktoś myśli, że algorytmy i programy komputerowe to jedno i to samo. Takie twierdzenie jest nieuprawnione. Istnieją różne sposoby opisu instrukcji do wykonania, o bardzo różnych poziomach szczegółowości:

Człowiek zrozumie instrukcję wypowiedzianą w języku naturalnym, np. „Proszę podać mi szklankę wody”. Komputery prawdopodobnie nie!

Pudełka z liczbami. Kliknij, by załadować.

Oto prosty przykład: Masz przed sobą pewną liczbę pudełek. W każdym jest ukryta inna liczba. Chcesz znaleźć największą liczbę. Rozwiązaniem jest sprawdzenie pudełek jedno po drugim i zapamiętywanie w każdym kroku największej znalezionej do tej pory liczby. Co to jednak miałoby znaczyć konkretnie dla komputera? Taki zwięzły opis metody będzie być może zrozumiały dla człowieka, ale bezużyteczny dla maszyny.

Algorytm to opis kolejnych kroków potrzebnych do poprawnego rozwiązania problemu (zadania).

Algorytm przyniesienia szklanki wody z kuchni można by zapisać jako listę kroków:
1) Idź do kuchni.
2) Weź szklankę.
3) Odkręć kran.
4) Podstaw szklankę i nalej wodę.
5) Zakręć kran.
6) Zanieś szklankę osobie, którą prosiła o wodę.
Choć opis jest szczegółowy, to jednak ciągle jest to język naturalny. Informatycy posługują się bardziej sformalizowanymi opisami.

Algorytmy komputerowe w podręcznikach często zapisuje się w postaci pseudokodu, który przypomina kod języka programowania, ale pozbawiony jest szczegółów technicznych, które są istotne wyłącznie dla programisty.

Zbiór pudełek jest ilustracją struktury danych. Informatyk powie, że przedstawia nieuporządkowaną tablicę (listę) liczb.

Algorytm znajdowania największej liczby w takiej nieuporządkowanej tablicy, zapisany w pseudokodzie, może wyglądać tak:

Jeżeli tablica jest pusta,
  to zakończ.
W przeciwnym przypadku zapamiętaj pierwszą wartość w tablicy.
Dla każdej z pozostałych wartości w tablicy wykonaj:
  Jeżeli ta wartość jest większa od zapamiętanej, 
    to zamień wartość pamiętaną na tę wartość.
Wyświetl zapmiętaną wartość.

Algorytmy zapisane w pseudokodzie lub jako lista kroków to ciąg jednoznacznych instrukcji, zrozumiałych dla informatyka; mimo to nie jest to jeszcze ten poziom precyzji sfmormułowań, jaki wymagany jest od instrukcji przeznaczonych do wykonania przez komputer.

Algorytm powinien być tak zapisany, na takim poziomie szczegółowości, żeby można było oszacować jego efektywność. Osoba, która przeanalizuje przedstawiony wyżej algorytm znajdowania największej wartości w tablicy, nie powinna mieć wątpliwości, że podwojenie rozmiaru tablicy skutkowałoby podwojeniem czasu wykonania. Taka wiedza ma ogromne znaczenie: algorytm jest wystarczająco szybki dla małych tablic wyników, ale niepraktyczny dla wielodostępnych (obługujących wielu użytkowników) systemów internetowych przetwarzających ogromne zbiory danych, które potrzebowałyby tablicy o milonach wyników.

Najbardziej precyzjnym sposobem zapisu listy instrukcji algorytmu jest kod źródłowy programu komputerowego, zapisany w konkretnym języku programowania. Taka forma zapisu algorytmu stanowi kod zrozumiały dla komputera.

Algorytm przyniesienia szklanki wody z kuchni można by zapisać w postaci programu komputerowego, który wykonałby robot. Oczywiście programista musiałby użyć języka programowania, który rozumie komputer wbudowany w robota.

Poniżej zapisano algorytm znajdowania największej liczby w tablicy (na liście). Użyto języka Python. Trzeba podkreślić, że nawet w tym jednym konkretnym języku programowania można by na wiele sposobów zapisać ten sam algorytm. Różni programiści mogliby zapisać pewne szczegóły techniczne w trochę inny sposób.

def znajdz_najwieksza(wyniki):
    if len(wyniki) == 0:
        print("Tabela jest pusta.")
        return -1
    else:
        najwiekszy = wyniki[0]
        for wynik in wyniki[1:]:
            if wynik > najwiekszy:
                najwiekszy = wynik
        return najwiekszy

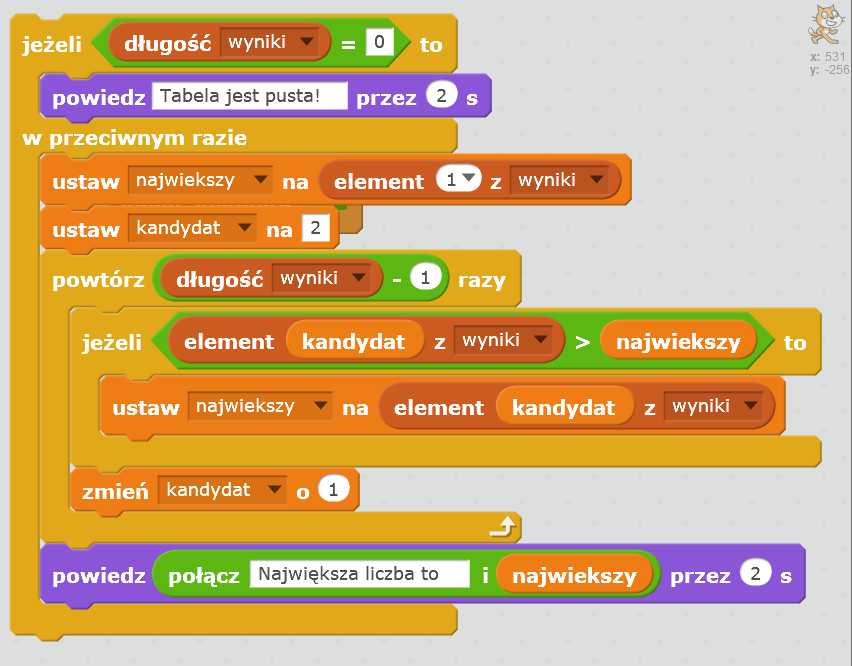
Poniżej ten sam algorytm przedstawiono w języku Scratch.

Oba programy realizują ten sam algorytm.

W tym rozdziale, w dalszej części, zajmiemy się algorytmami bardziej szczegółowo. Pojęcie algorytmu jest fundamentalne w informatyce. Interesować będą nas algorytmy same w sobie, a nie ich konkretne komputerowe realizacje.

Kiedy informatycy porównują dwa algorytmy rozwiązujące ten sam problem, to często używają określenia „koszt algorytmu”. Mówi się o zależności szybkości algorytmu od rozmiaru danych wejściowych (oznaczmy ten rozmiar jako n). W tym rozdziale koszt działania algorytmu będziemy mierzyć albo badając czas wykonania programu (realizującego algorytm), albo zliczając liczbę kroków, operacji podstawowych algorytmu.

Zazwyczaj analizując algorytm, wyróżnia się operacje dominujące, najbardziej kosztowne, tzn. takie dla których koszt wykonania przez komputer jest większy od innych. Szacując koszt algorytmu, zlicza się takie operacje. W przypadku algorytmów wyszukiwania największej liczby w tablicy jest to porównywanie dwóch liczb. Okazuje się, że jeśli tablica składa się z 10 elementów, to takich porównań wykonuje się 10. Podwojenie liczby elementów tablicy prowadzi do podwojenia liczby operacji. Można więc powiedzieć, że liczba operacji jest proporcjonalna do n. Nie wszystkie algorytmy mają tę własność; niektóre algorytmy są o wiele bardziej kosztowne, a niektóre mniej; Warto, aby programista potrafił określić szybkość algorytmu, zanim zdecyduje się nim posłużyć np. w kodzie oprogramowania internetowego, z którego będzie korzystać wielu użytkowników jednocześnie. Gra komputerowa, którą programista stworzył, może okazać się bardzo popularna, więc algorytm znajdowania najlepszego wyniku musi być wystarczająco szybki.

Trzeba podkreślić, że czas potrzebny różnym komputerom do realizacji tego samego algorytmu i tych samych danych może być różny. Zależy to od parametrów komputerów, ilości zasobów przydzielonych do wykonania zadania, ale i od języka programowania, w którym algorytm został zakodowany. Dlatego trzeba być ostrożnym w wyciąganiu pochopnych wniosków o koszcie algorytmu tylko na podstawie czasu wykonania programu.

Znacznie lepszą miarą jest zliczanie operacji (takich jak porównywanie dwóch wartości), które są właściwe danemu algorytmowi.

W tym rozdziale przyjrzymy się dokładniej dwu najważniejszym typom algorytmów: przeszukiwania i porządkowania danych. Prawdopodobnie każdy z nas z jednym z tych typów problemów już się musiał zmierzyć, być może nie do końca świadomie!

Na przykładach tych typów algorytmów można w ciekawy sposób przedstawić kluczowe koncepcje projektowania i analizy algorytmów.

Przeszukiwanie różnych zbiorów danych zajmuje znaczącą część pracy wielu komputerów. Gdy używasz wyszukiwarki Google'a prowadzisz dialog z programem przeszukującym indeksy baz danych na serwerach wyszukiwarki. Komputery często muszą przetwarzać ogromne ilości danych, a to oznacza, że potrzebują szybkich algorytmów.

Zdobywanie wiedzy na ten temat zacznij od poniższej zabawy...

Przeszukiwanie pudełek -- część 1. Kliknij, by załadować.

Cechą charakterystyczną tej gry było losowe rozmieszczenie liczb. Skutek był taki, że sukces zależał od szczęścia! Wyobraź sobie, że pudełek jest 1000, czy nawet 1 000 000! Przeszukiwanie takich zbiorów trwałoby długo.

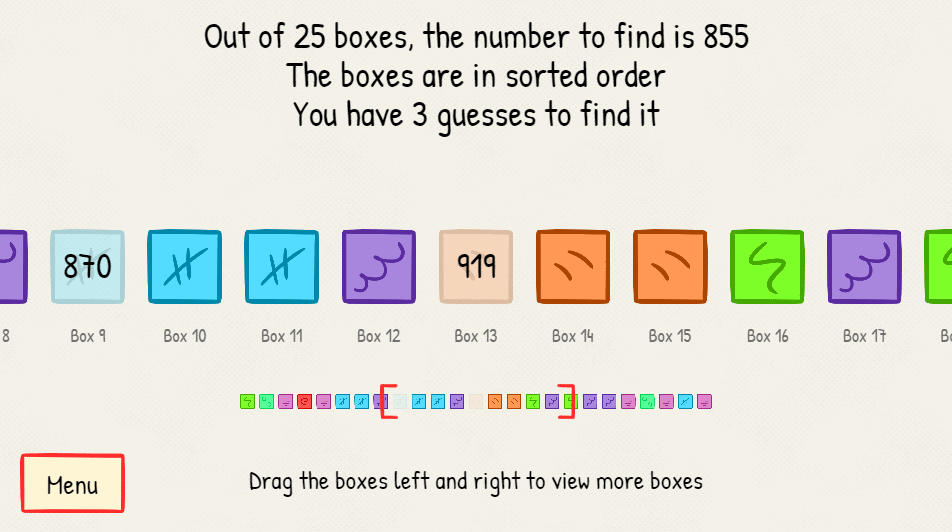
Kolejna wersja ćwiczenia różni się od poprzedniej. Liczba dopuszczalnych prób będzie mniejsza, ale tym razem liczby będą rozmieszczone od najmniejszej (po lewej) do największej (po prawej). Spróbuj się uporać z zadaniem!

Przeszukiwanie pudełek -- część 2. Kliknij, by załadować.

Dlaczego w drugiej wersji zawsze wygrywasz? Na czym opiera się zwycięska strategia?

W pierwszej z gier pudełka ustawione były w przypadkowej kolejności. Trudno więc mówić o stosowaniu jakiejkolwiek strategii przeszukiwania. Konieczne było sprawdzanie pudełek jedno po drugim, aż do skutku. W informatyce mówi się w takim przypadku o przeszukiwaniu liniowym (czasami o przeszukiwaniu sekwencyjnym). Taki algorytm można by opisać listą kroków:

• Sprawdź, czy pierwszy element listy jest tym, który jest poszukiwany. Jeśli tak, to zakończ przeszukiwanie.
• W przeciwnym przypadku sprawdź kolejny element listy.
• Kontynuuj przeszukiwanie, aż znajdziesz element, który jest poszukiwany lub sprawdzisz wszystkie elementy listy.

W przypadku przeszukiwania listy 10 elementów, średnia liczba prób prowadzących do sukcesu to 5. Dla listy 10 000 elementów tych prób będzie średnio 5000. Oczywiście w konkretnym przypadku liczba prób może być mniejsza od średniej, nawet znacznie mniejsza, albo i większa. W najgorszym przypadku przeszukiwania nie można wykonać szybciej niż przez sprawdzenie wszystkich elementów listy. Można uzasadnić, że algorytm opisany jak wyżej jest pod tym względem optymalny.

W drugiej z gier pudełka były uporządkowane, co umożliwiło podejmowanie kolejnych prób w sposób przemyślany. Być może nieświadomie ktoś stosował algorytm zwany w informatyce przeszukiwaniem binarnym (dwudzielnym).

Algorytm przeszukiwania binarnego można opisać listą kroków:

• Sprawdź, czy element znajdujący się w środku listy jest tym, który jest poszukiwany. Jeśli tak, to zakończ przeszukiwanie.
• W przeciwnym przypadku: Jeśli ten środkowy element ma wartość większą od poszukiwanego, to w dalszych przeszukiwaniach pomiń elementy listy po prawej stronie środkowego. (Jeśli lista jest uporządkowana od nawiększego do najmniejszego, to pomiń elementy po lewej.) Jeśli ten środkowy element ma wartość mniejszą od poszukiwanego, to w dalszych poszukiwaniach pomiń elementy mniejsze od środkowego.
• Kontynuuj przeszukiwanie, aż znajdziesz element, który jest poszukiwany.

Trzeba pamiętać, że przeszukiwanie binarne można stosować tylko dla zbiorów uporządkowanych. To oznacza, że algorytmy porządkowania należy uznać za jeszcze ważniejsze!

Komputery często muszą porządkować duże zbiory danych. Kryteria porządkowania mogą być różne, mogą się zmieniać. Użytkownik komputera czasami chce zobaczyć listę plików uporządkowaną według nazw, a czasem według rozmiaru itp. Lista klientów zwykle jest porządkowana według nazwisk. Uporządkowanie danych ułatwia ich przeszukiwanie. Jak zwykle uporządkowane są informacje w spisie pracowników dużej firmy? Według nazwiska, czy według numerów telefonów? Dlaczego?

Wymyślono wiele algorytmów porządkowania. W tym podrozdziale przedstawione będą trzy: dwa mniej efektywne i jeden bardzo szybki.

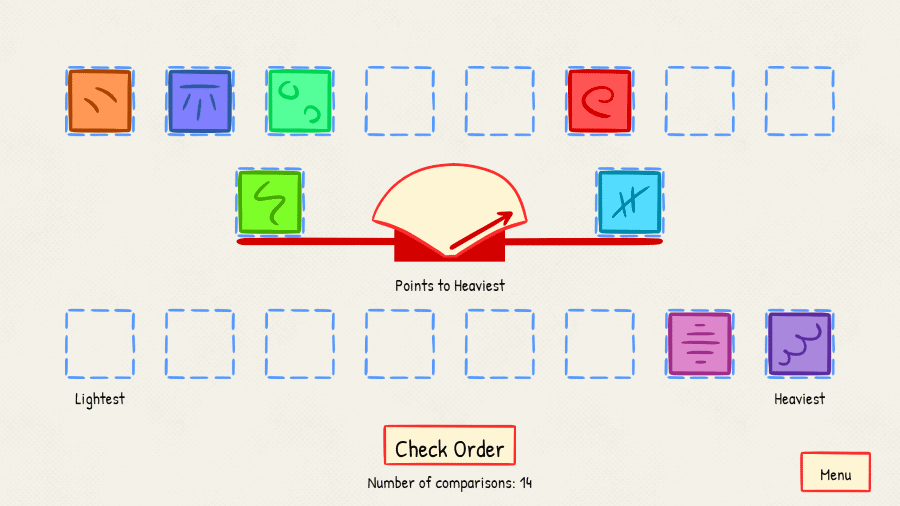
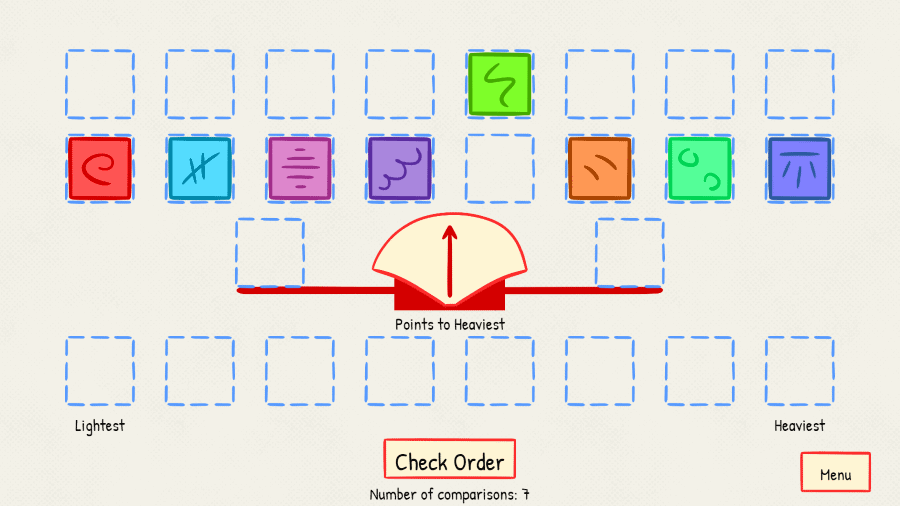
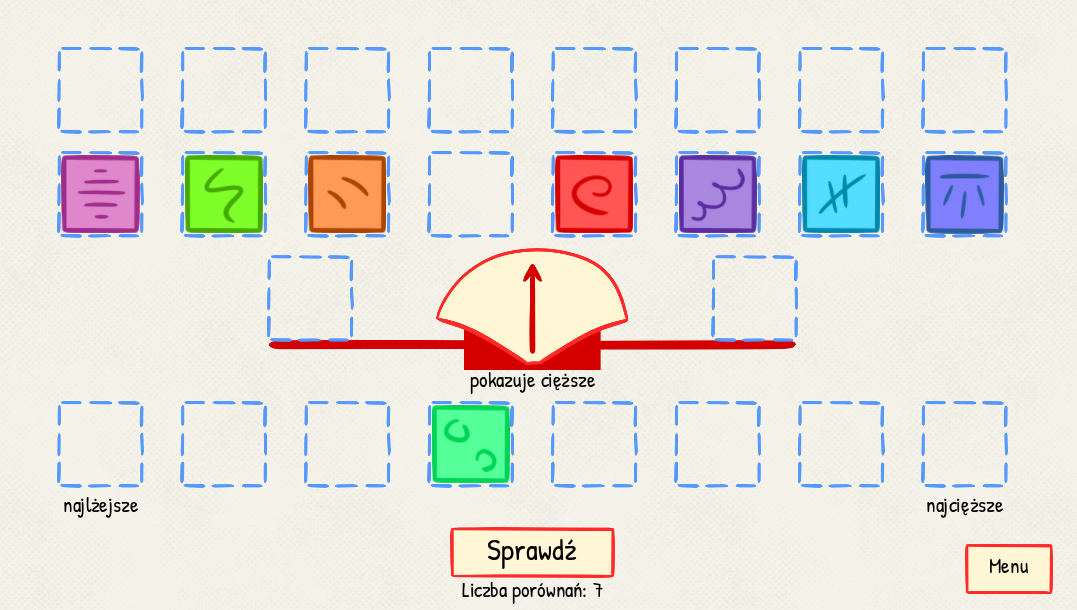
Poniżej udostępniamy aplikację z wirtualną wagą szalkową do testowania algorytmów opisanych poniżej. U dołu ekranu pojawia się informacja o liczbie porównań (ważeń): każde ważenie to jedno porównanie. Koszt algorytmu będzie określony liczbą porównań użytych do uporządkowania 8 pudełek. Zakładamy, że na każdej szalce wagi kładzie się jedno pudełko.

Pudełka należy uporządkować od najlżejszego po lewej do najcięższego po prawej. Do sprawdzenia użyj przycisku SPRAWDŹ.

Możesz posłużyć się prawdziwą wagą szalkową. Odważniki trzeba tak przygotować, żeby żadne dwa nie ważyły tyle samo.

Waga szalkowa. Kliknij, by załadować.

Jednym z najbardziej intuicyjnych sposobów rozpoczęcia porządkowania jest: zacząć od znalezienia najlżejszego (lub najcięższego) pudełka i odłożyć je na bok. Spróbuj to zrobić z użyciem wagi szalkowej. Zapisz liczbę wykonanych porównań.

Po znalezieniu najlżejszego pudełka znajdź drugie najlżejsze pudełko w ten sam sposób i ustaw je obok najlżejszego. Zapisz liczbę porównań. Powtarzaj poszukiwanie kolejnych najlżejszych, na danym etapie, pudełek, aż wszystkie pudełka będą uporządkowane. Zapisuj liczbę porównań. Ile porównań (ważeń) zostało wykonanych?

Wskazówka: Zacznij od przeniesienia wszystkich pudełek na prawą stronę ekranu. (Jeśli szukasz najcięższego, to przenieś pudełka na lewą stronę ekranu.)

Przeanalizuj notatki dotyczące liczby porównań. Dostrzegasz jakąś prawidłowość? Ile porównań było wykonywanych w kolejnych etapach wybierania najlżeszych pudełek? Ile porównań łącznie byłoby wykonanych, gdybyśmy porządkowali zbiór 9 pudełek? Ile dla 20 pudełek? Załóżmy, że wiesz, ile porównań potrzeba do uporządkowania 1000 pudełek tym algorytmem. O ile więcej byłoby potrzebnych, gdyby pudełek było 1001?

Przedstawiony wyżej algorytm nazywa się porządkowaniem przez wybór (selekcję). Ten algorytm można tak opisać listą kroków:

• Znajdź najmniejszy element na liście. Umieść go na początku nowej listy.
• Znajdź najmniejszy element wśród pozostałych na liście. Umieść go na drugiej liście obok elementu ustawionego tam po poprzednim przeszukiwaniu.
• Kontynuuj przeszukiwanie listy, aż wszystkie elementy znajdą się na drugiej liście. Ta lista będzie uporządkowana.

W powyższym opisie można zastąpić słowo „najmniejszy” słowem „największy” i algorytm będzie nadal poprawny. Oczywiście w tym przypadku porządek elementów na liście będzie odwrócony (od największego do najmniejszego).

Algorytm porządkowania przez wybór można by tak zmodyfikować, że działałby w miejscu (z łaciny: in situ), to znaczy bez drugiej listy. Wymaga to zastosowania w algorytmie operacji zamiany dwóch elementów miejscami.

Algorytm działa w oparciu o następujący pomysł: Wybrane pudełko wyjmujemy z zbioru nieuporządkowego i wstawiamy na właściwej pozycji w zbiorze elementów wcześniej uporządkowanych. Podobnie jak porządkowanie przez wybór, algorytm przez wstawienie jest bardzo intuicyjny i ludzie często mniej lub bardziej świadomie stosują go, gdy porządkują jakiś zbiór obiektów lub np. karty do gry trzymane w ręce.

Spróbuj poćwiczyć algorytm z użyciem wagi szalkowej. Rozpocznij od przeniesienia wszystkich pudełek na jedną stronę ekranu. Następnie wybierz pudełko losowo i umieść je po drugiej stronie ekranu.

Aby znaleźć właściwe miejsce do wstawienia kolejnego pudełka, porównaj je z pudełkiem ustawionym wcześniej. W razie potrzeby zmień kolejność pudełek. Kolejne wstawiane pudełka należy umieścić we właściwym miejscu. Jedyną dozwoloną operacją jest porównywanie dwóch pudełek. Zliczaj liczbę wykonanych porównań (ważeń)!

Ten algorytm nazywa się algorytmem porządkowania przez wstawianie. Dla lepszego zrozumienia tematu warto obejrzeć tę animację z Wikipedii.

Ten algorytm można tak opisać listą kroków:

• Wybierz pierwszy element z listy. Umieść go na początku nowej listy.
• Wybierz pierwszy element spośród pozostałych na liście. Umieść go na drugiej liście we właściwym miejscu.
• Powtarzaj krok drugi, aż wszystkie elementy znajdą się na drugiej liście. Ta lista będzie uporządkowana.

Operację umieszczania elementu we właściwym miejscu na liście uporządkowanej można realizować mniej lub bardziej efektywnie: przez przeszukiwanie liniowe lub przeszukiwanie binarne.

Algorytm porządkowania przez wstawianie również można by tak zmodyfikować, że działałby w miejscu.

W praktyce algorytm porządkowania przez wstawianie dla dużych zbiorów danych wymaga zwykle znacznej liczby operacji zamiany dwóch elementów miejscami. Te operacje są kosztowne. Dlatego metoda przez wstawianie nie znajduje zwykle zastosowania w komputerowej realizacji porządkowania danych.

W przypadku dużych zbiorów danych algorytmy porządkowania przedstawione wcześniej wymagają wykonania stosunkowo dużej liczby porównań (wyjątkiem jest porządkowanie przez binarne wstawianie).

W praktycznych zastosowaniach zazwyczaj o wiele lepszym algorytmem porządkowania jest metoda zwana po angielsku Quicksort

Quicksort. Kliknij, by załadować.

Ten algorytm jest trochę bardziej skomplikowany, ale bardzo efektywny. Przekonaj się o tym, wykonując eksperyment z wykorzystaniem wirtualnej lub prawdziwej wagi szalkowej. Wybierz pudełko losowo i umieść je na jednej z szalek wagi. Następnie porównaj je z każdym z pozostałych pudełek; cięższe powinny być odkładane po prawej stronie, a lżejsze po lewej. Na końcu tego etapu wybrane początku pudełko umieść pomiędzy dwa zbiory lżejszych i cięższych, w rzędzie poniżej. Ile było porównań? Zauważ, że to pudełko jest już na właściwym miejscu docelowego zbioru uporządkowanego.

Kolejny etap to powtórzenie opisanej wyżej procedury dla każego z dwóch ustalonych wcześniej zbiorów pudełek (lżejszych i cięższych). Następnie procedurę należy powtarzać wielokrotnie dla nowo ustalonych zbiorów. Aż wszystkie pudełka są we właściwej kolejności!

Warto powtórzyć cały eksperyment z wagą kilkukrotnie. Dlaczego? Dlatego, że wiele zależy od szczęścia, to znaczy od wyboru pierwszego pudełka. W przypadku pecha może się okazać, że to kluczowe pudełko jest najcieższe lub najlżejsze wśród wszystkich. W przypadku szczęścia wybrane pudełko będzie tym, które w zbiorze uporządkowanym znajdzie się pośrodku. Krótko mówiąc: Całkowita liczba porównań może być różna w każdym z eksperymentów.

Ten algorytm można tak opisać listą kroków:

• Wybierz losowo element z listy i porównaj go z wszystkimi pozostałymi elementami (ten element czasami nazywa się osiowym).
• Zgrupuj wszystkie elementy o mniejszej wartości po lewej stronie elementu osiowego, a wszystkie elementy o większej wartości po prawej stronie.
• Wybierz jedną z nieposortowanych podgrup i powtórz proces opisany w krokach powyżej. Proces jest przerywany, gdy wszystkie powstałe podgrupy są już jednoelementowe.

Istnieją krocie różnych algorytmów porządkowania. Większość tych istotnie praktycznych jest oparta na dwóch algorytmach: porządkowaniu szybkim (quicksort) i porządkowaniu przez scalanie (mergesort). Te, oraz wiele innych, możesz zobaczyć na poniższym wideo.

Ten rozdział to tylko wprowadzenie do tematu algorytmów. Istnieją z pewnością tysiące algorytmów dla tysięcy różnych zadań! Algorytmy są podstawą rozwiązywania problemów w wielu dziedzinach informatyki praktycznej (np. sztucznej intelignecji, rozpoznwania obrazów, wyznaczania najkrótszej trasy) i innych dziedzinach. Dzięki zrozumieniu kluczowych pojęć łatwiej będzie zrozumieć trudniejsze pojęcia na studiach.

Warto podkreślić, że istnieją inne metody przeszukiwania (np. z haszowaniem, drzewa przeszukiwań) i porządkowania (np. przez łączenie), które w konkretnej sytuacji mogą być bardziej efektywne od przedstawionych w tym rozdziale. Informatyk powinien je poznać, by szukając rozwiązania rzeczywistego problemu nie „wyważał otwartych drzwi”, a dostosowywał do konkretnej sytuacji algorytmy o utrwalonej renomie.

Na koniec dodajmy, że komputerowe realizacje algorytmów korzystają z rejestrów procesora (pamięci cache), ale też czasem z tzw. wirtualnej pamięci (dysku komputerowego), a więc czas dostępu do konkretnej wartości może być bardzo krótki, ale też bardzo długi. Te różne uwarunkowania wymagają od projektantów systemów komputerowych stosowania algorytmów, które w danej sytuacji są najbardziej efektywne.

• Istnieje metoda przeszukiwania zbiorów danych, lepsza od przeszukiwania binarnego. Nazywa się haszowaniem (ang. to hash oznacza posiekać). Łagodne wprowadzenie do tematu znajdziesz w materiałach Gra w statki, opisanej w scenariuszu 6 w zbiorze scenariuszy lekcji bez komputera.
• Istnieją problemy, dla których nie znaleziono dobrych algorytmów, a nawet takie, których prawdopoodbnie nigdy nie da się rozwiązać w efektywny sposób. Więcej na ten temat piszemy w rozdziale o złożoności obliczenionej algorytmów i praktycznej wykonalności algorymów.

Wszystkie poniższe materiały edukacyjne, poza ostatnim, są po angielsku.

• CS Unplugged i algorytmy przeszukiwania;
• CS Unplugged i algorymy sortowania;
• ćwiczenie na temat przeszukiwania metodą „Dziel i rządź” (w literaturze nazywaną częściej „Dziel i zwyciężaj”, z powodu nazwy angielskiej Divide and Conquer) na stronie CS Unplugged;
• przeszukiwanie liniowe, przeszukiwanie binarne, sortowanie przez wybór, sortowanie przez wstawianie i Quicksort w artykułach Wikipedii;
• sortowanie cegieł (gra) do nauki algorytmów sortowania (wymaga obługi Javy przez przeglądarkę);
• wizualizacja algorytmów sortowania przedstawiająca różne algorytmy sortowania, zapisane w pseudokodzie;
• notacja asymptotyczna.