-
Dla nauczyciela. Duże liczby na horyzoncie!
W tym rozdziale pojawiają się bardzo duże liczby, zwłaszcza w kontekście problemu wykładniczej eksplozji czasu. Wiele zasobów ilustruje te koncepcje. Można pobrać wideo The Power of Exponentials, Big and Small z MIT, które ilustruje wykładniczy wzrost za pomocą zabawnych przykładów.
Czy istnieją problemy, które są zbyt trudne nawet dla komputerów? Okazuje się, że tak. W rozdziale na temat sztucznej inteligencji zobaczymy, że zwykłe prowadzenie rozmowy jest czymś, z czym komputery nie radzą sobie dobrze, nie dlatego, że nie potrafią mówić, ale raczej dlatego, że niczego nie rozumieją ani nie mają niczego rozsądnego do powiedzenia. Jednak nie o takie trudne problemy nam tu jednak chodzi -- to nie tak, że komputery nie mogłyby prowadzić rozmów, tylko sami nie wiemy, jak to robimy, więc nie możemy powiedzieć komputerowi co ma robić.
W tym rozdziale przyjrzymy się problemom, w których łatwo jest powiedzieć komputerowi, co należy zrobić -- pisząc program -- ale komputer nie jest w stanie zrobić tego, czego chcemy, ponieważ zajmuje to zbyt wiele czasu: może nawet miliony wieków. Kupno szybszego komputera też niewiele daje: gdyby był sto razy szybszy, to i tak zajmie miliony lat; nawet milion razy szybszy zająłby setki lat. To się nazywa trudny problem -- taki, w którym znalezienie rozwiązania trwa dłużej niż czas życia najszybszego komputera, jaki można sobie wyobrazić!
Dziedzina wykonalności obliczeniowej bada problemy i algorytmy, które mogą wymagać niemożliwych ilości obliczeń, być może za wyjątkiem bardzo małych instancji problemu.
Zdefiniujemy, co rozumiemy przez praktycznie wykonalny później, a teraz, ujmując to w sposób uproszony, powiemy tylko, że problem praktycznie wykonalny to taki, dla którego potrafimy napisać programy rozwiązujące go w rozsądnym czasie, a problem trudny to taki, gdzie program musiałby działać o wiele za długo.
Wiedza o tym, że problem, który próbujesz rozwiązać, jest jednym z tych trudnych problemów, jest bardzo ważna. W przeciwnym razie łatwo jest zmarnować masę czasu, starając się wymyślić sprytny program, aby go rozwiązać, do niczego nie dochodząc. Informatyk musi być w stanie rozpoznać że problem jest trudny, żeby skorzystać z innych podejść. Bardzo powszechnym podejściem jest rezygnacja z uzyskania dokładnego rozwiązania, a zamiast tego dążenie do uzyskania rozwiązania przybliżonego. Istnieje wiele technik uzyskiwania dobrych przybliżonych rozwiązań dla trudnych problemów; sposób rozwiązywania, który nie gwarantuje otrzymania najlepszego wyniku, jest czasami określany jako heurystyczny.
Jednym z ważnych przykładów trudnego problemu, którym zajmujemy się w tym rozdziale, jest problem komiwojażera (ang. Travelling Salesman Problem, w skrócie TSP). Łatwo go opisać; jeśli masz listę miast, które musisz odwiedzić, i znasz odległość między każdą parą miast, jaka jest najkrótsza trasa, która odwiedza wszystkie miasta dokładnie raz? Jest to bardzo praktyczny problem, który pojawia się, gdy pojazdy kurierskie wybierają trasy dostarczania paczek, zespoły rockowe planują trasy koncertowe, a nawet gdy wyznaczony, trzeźwy kierowca, rozwozi przyjaciół po imprezie. W rzeczywistości miara między miastami nie musi być odległością. Może to być koszt podróży między każdą parą miast. Na przykład, jeśli chcesz odwiedzić Queenstown, Christchurch, Auckland i Wellington, minimalizując koszty biletów lotniczych, a znasz koszt przelotu między każdą parą tych 4 miast, to możesz wyliczyć jak je oblecieć najtaniej. Jest to nadal przykład TSP. Można go również zastosować do problemów, które nie dotyczą podróży; na przykład został użyty do opracowania sposobu wydajnej syntezy DNA (artykuł w języku angielskim).
Poniższa aplikacja rozwiązuje problem dla tylu miast, ile tylko wybierzesz, próbując wszystkich możliwych tras i pamiętając najlepszą do tej pory znalezioną. Możesz poczuć jak wygląda trudny problem, sprawdzając jak długo program rozwiązuje zadanie na mapach o różnych rozmiarach. Spróbuj wygenerować mapę z około 5 miastami i naciśnij ,,Start'', aby rozwiązać zadanie.
Teraz spróbuj 10 miast (dwa razy więcej). Czy trwa to dwa razy dłużej? Co powiesz na jeszcze dwa razy więcej (20 miast)? A co z 50 miastami? Czy wiesz, ile czasu to zajmie? Zaczynasz czuć, co to znaczy, że problem jest trudny.
Oczywiście, w niektórych sytuacjach, trudne problemy są dobre. W szczególności większość algorytmów dotyczących bezpieczeństwa i kryptografii opiera się na trudnych do rozwiązania problemach; kody mogłyby zostać złamane, ale zajęłoby to miliardy lat, a więc to daremny trud. W rzeczywistości, jeśli ktokolwiek znajdzie szybki algorytm rozwiązywania takich problemów, wiele systemów bezpieczeństwa komputerowego z dnia na dzień przestałoby być bezpieczne! Dlatego jednym z zadań informatyków jest upewnienie się, że takie rozwiązania nie istnieją!
W tym rozdziale przyjrzymy się TSP i innym problemom, dla których nie są znane efektywne rozwiązania, problemom, które komputery liczyłyby miliony stuleci. I napotkamy dziś coś, co z pewnością jest największą tajemnicą informatyki: że nikt nie wie czy istnieje skuteczniejszy sposób rozwiązania tych problemów! Możliwe, że nikt jeszcze nie wymyślił dobrego sposobu, a może go nie ma. Nie wiemy jak jest naprawdę.
Zacznijmy jednak od znanego problemu, który możemy rozwiązać.
Złożoność obliczeniowa to ważne pojęcie dotyczące problemów i algorytmów, które je rozwiązują. Zwykle złożoność to po prostu czas potrzebny do rozwiązania problemu, ale istnieje kilka sposobów mierzenia ,,czasu''. Mierzenie rzeczywistego czasu na danym komputerze może być przydatne, ale aby uzyskać przybliżone pojęcie o zachowaniu właściwemu danemu algorytmowi, informatycy często zaczynają od oszacowania liczby kroków, jakie algorytm wykona dla n elementów. Na przykład wyszukiwanie liniowe może wymagać sprawdzania każdego z n elementów, więc algorytm wykona n kroków. Algorytm, który porównuje każdą parę wartości z listy n elementów, będzie musiał dokonać \(n^2\) porównań, więc możemy scharakteryzować go jako wymagającego około \(n^2\) kroków. Daje nam to dużo informacji o tym, jak dobry jest algorytm, bez wchodzenia w szczegóły typu: na jakim komputerze był uruchomiony, w jakim był języku i jak dobrze napisano program. Termin złożoność jest używany w odniesieniu do tych przybliżonych miar.
Zgrubne pojęcie o złożoności problemu pomaga oszacować, ile czasu zajmie jego rozwiązanie. Na przykład, jeśli piszesz program i uruchamiasz go z prostymi danymi wejściowymi, ale jeszcze po 10 minutach się nie zakończył, czy powinieneś przerwać, czy zaraz się skończy? Dobrze, jeśli potrafisz oszacować liczbę kroków, które musi wykonać, a następnie oszacować czas działania na podstawie czasu, w jakim inne programy szukają podobnych rozwiązań.
-
Co to znaczy?. Asymptotyczna złożoność
Gdy będziesz czytać o złożoności, możesz natknąć się na terminologię taką jak np. notacja ,,duże O'' i asymptotyczna złożoność, wedle której algorytm, który zajmuje około \(n^2\) kroków jest określany jako \(O(n^2)\). Nie zajmiemy się nimi w tym rozdziale, ale poniżej jest garść informacji na wypadek, gdybyś zetknął się z tymi pojęciami gdzie indziej. Notacja ,,duże O'' pozwala mówić o złożoności i jest używana z asymptotyczną złożonością, która po prostu oznacza, jak algorytm działa dla dużych wartości n. ,,Asymptotyczna'' oznacza, że n staje się naprawdę duże -- kiedy tak się dzieje, mniej się martwimy drobnymi szczegółami, jeśli chodzi o czas pracy. Jeśli algorytm kończy działanie po siedmiu dniach, to zupełnie nie jest interesujące, że w rzeczywistości jest to 7 dni, 1 godzina, 3 minuty i 4,33 sekundy, i nie warto tracić czasu na dokładne badanie.
Nie użyjemy precyzyjnej notacji asymptotycznej złożoności (która mówi, którą część obliczeń szybkości można bezpiecznie zignorować), ale dokonamy przybliżonych oszacowań liczby operacji, które wykona algorytm. Nie trzeba się zbytnio przejmować precyzją, ponieważ informatykom wystarczy prosta charakterystyka, która daje ogólne pojęcie o szybkości.
Na przykład rozważmy użycie algorytmu sortowania przez wybór, aby posortować rosnąco listę n liczb. (Jest to wyjaśnione w rozdziale dotyczącym algorytmów). Załóżmy, że ktoś powiedział Ci, że sortowanie tysiąca pozycji zajęło 30 sekund. Czy to wygląda na dobry algorytm? Po pierwsze, pewnie chciałbyś wiedzieć, na jakim komputerze działał - jeśli to superkomputer, to nie jest za dobrze; jeśli to maleńkie urządzenie o małej mocy, takie jak smartfon, to może jest nieźle.
Ponadto, ta pojedyncza wartość nie mówi o tym, jak dobrze system będzie sobie radził z większymi zadaniami. Gdyby powyższy algorytm dostał 10 tysięcy elementów do posortowania, prawdopodobnie zajęłoby to około 50 minut (3000 sekund) -- przetworzenie 10 razy więcej danych wejściowych zajmie 100 razy dłużej.
Te zmierzone czasy dla konkretnego komputera są przydatne, żeby nabyć wyczucia co do wydajności (to znaczy złożoności) algorytmu, ale nie dają jasnego obrazu. Okazuje się, że możemy dokładnie określić, ile kroków zajmie algorytm sortowania przez wybór dla n elementów: będzie wymagał około \(\frac{n(n-1)}{2}\) działań, czyli w rozszerzonej formie \(\frac{n^2}{2} - \frac{n}{2}\). Ten wzór ma zastosowanie niezależnie od komputera, na którym działa algorytm, i chociaż nie powie nam, ile czasu zajmie rozwiązanie, to może pomóc nam stwierdzić, czy będzie do przyjęcia.
Z powyższego wzoru wynika, dlaczego przy dużych wartościach n robi się niedobrze: liczba kroków wzrasta wraz z kwadratem wielkości wejścia. Wstawienie wartości 1 tysiąca za n mówi nam, że będzie \(1000000/2 - 1 000/2\), czyli 499 500 kroków.
Zauważ, że druga część (1000/2) daje niewielką różnicę w obliczeniach. Jeśli użyjemy tylko pierwszej części wzoru, czyli \(\frac{n^2}{2}\), to oszacowanie zmieni się tylko o 0,1%, a szczerze mówiąc, użytkownik nie zauważy, czy będzie 20 czy 19,98 sekund. To istota asymptotycznej złożoności -- musimy tylko skupić się na najważniejszej części wzoru, która zawiera \(n^2\).
Ponadto, ponieważ pomiar liczby kroków jest niezależny od komputera, na którym algorytm będzie działać, nie ma znaczenia, czy jest on opisany jako \(\frac{n^2}{2}\) czy \(n^2\). Ilość czasu, jaki zajmie, będzie proporcjonalna do obu tych wielkości, więc równie dobrze możemy go uprościć do \(n^2\). Charakteryzuje to algorytm sortowania przez wybór jedynie w sposób przybliżony, ale to już wiele nam o nim mówi, a ten poziom dokładności jest szeroko stosowany do szybkiego, ale dość dokładnego scharakteryzowania złożoności algorytmów. W tym rozdziale będziemy posługiwać się podobnymi, zgrubnymi charakterystykami, ponieważ zwykle to wystarcza, aby się zorientować czy algorytm zakończy się w rozsądnym czasie, czy też nie.
Jeśli uczyłeś się kiedyś o algorytmach, dowiedziałeś się, że niektóre algorytmy sortowania, takie jak sortowanie przez scalanie i sortowanie szybkie (ang. Quicksort), są z natury szybsze niż inne algorytmy, takie jak sortowanie przez wstawianie, sortowanie przez wybór, czy sortowanie bąbelkowe. Oczywiście lepiej jest używać szybszych.
Zasadniczo konsekwencją zastosowania niewłaściwego algorytmu sortowania będzie to, że użytkownik będzie czekać wiele minut (a może godzin), a nie kilka sekund lub minut.
Tutaj rozważymy inny algorytm sortowania, nazywany sortowaniem przez permutacje. Przebiega on tak: ,,Wymieńmy wszystkie możliwe porządki (,,permutacje'') elementów, które mają zostać posortowane, i sprawdzajmy każdy z nich po kolei, aż znajdziemy ten, w którym elementy są posortowane''. Ten algorytm prosto opisać, ale czy jest on dobry?
-
Dla nauczyciela. Sortowanie przez permutacje nie jest w praktyce użyteczne!
Zauważ, że sortowanie przez permutacje nie jest w ogóle rozsądnym sposobem sortowania; to tylko przykład, który pomaga nam myśleć o wykonalności algorytmu. Dla uczniów powinno być oczywiste, że jest ono rażąco nieefektywne. Najważniejsze jest to, że daje właściwy wynik, więc jest to skrajny przykład algorytmu, który działa poprawnie, ale jest zbyt nieefektywny, by był przydatny.
Na przykład, jeśli sortujesz liczby 45, 21 i 84, wtedy wszystkie możliwe kolejności, w jakich można je ustawić (to znaczy wszystkie permutacje) to:
45, 21, 84
45, 84, 21
21, 45, 84
21, 84, 45
84, 21, 45
84, 45, 21
Patrząc na powyższą listę widzimy, że jedynym uporządkowanym wierszem jest 21, 45, 84, więc to jest rozwiązanie. Jest to bardzo nieefektywne podejście, ale pomoże zilustrować, co rozumiemy pod pojęciem wykonalności.
Aby zrozumieć, jak to działa i jakie są tego konsekwencje, wybierz cztery różne słowa (w poniższym przykładzie użyliśmy kolorów) i wypisz wszystkie możliwe uporządkowania tych czterech słów. Każde słowo powinno pojawić się dokładnie raz w każdym uporządkowaniu. Możesz to zrobić samodzielnie lub użyć internetowego generatora permutacji, takiego jak JavaScriptPermutations lub Text Mechanic.
Na przykład, jeśli wybrałeś czerwony, niebieski, zielony i żółty, pierwsze kilka uporządkowań może mieć taką postać:
- czerwony, niebieski, zielony, żółty
- czerwony, niebieski, żółty, zielony
- czerwony, żółty, niebieski, zielony
- czerwony, żółty, zielony, niebieski
Nie muszą być w żadnej określonej kolejności, chociaż zalecamy podejście systematyczne, żeby o żadnym nie zapomnieć!
-
Dla nauczyciela. Rozwiązanie
Dla czterech różnych słów, będzie 4x3x2x1=24 różnych uporządkowań. Na przykład, sześć z nich zaczyna się od ,,czerwony'', sześć zaczyna się od ,,niebieski'' i tak dalej.
Gdy lista permutacji zostanie utworzona, wyszukaj w niej permutację, która ma słowa posortowane w kolejności alfabetycznej. Proces, który właśnie zakończyłeś, używa sortowania przez permutacje do sortowania słów.
Teraz dodaj kolejne słowo. Ile będzie możliwych uporządkowań pięciu słów? A co w przypadku dwóch i trzech słów -- ile jest ich uporządkowań? Jeśli dasz za wygraną przy wypisywaniu wszystkich uporządkowań pięciu słów, czy możesz wyliczyć ile ich jest? Czy znalazłeś wzór? Jak myślisz, ile może być uporządkowań dziesięciu słów? (Nie musisz ich wypisywać!)
-
Dla nauczyciela. Rozwiązanie
Liczba uporządkowań (permutacji) n słów to n silnia; jest to wyjaśnione poniżej, ale w skrócie: istnieje n opcji dla pierwszego słowa, n − 1 dla następnego, i tak dalej. Na przykład dla 15 słów jest 15 x 14 x 13 x 12 x ... x 1 permutacji, co wynosi 1 307 674 368 000. To duża liczba!
Silnię liczby można obliczyć za pomocą arkusza kalkulacyjnego (w Excelu formuła dla \(15!\) to =FACT(15). Wiele kalkulatorów ma przycisk z silnią ("!"). Można nawet wpisać \(15!\) do wyszukiwarki Google i uzyskać odpowiedź. Ale ten przewodnik ma prosty kalkulator, który działa na wielkich liczbach:
Jeśli chodzi o powyższe pytania, liczba permutacji to:
- 5 słów: 120 permutacji
- 2 słowa: 2 permutacje (tylko oryginalne dwie wartości i odwrotnie)
- 3 słowa: 6 permutacji
- 10 słów: 3 628 800 permutacji
Jeśli nie znalazłeś wzoru liczby uporządkowań, pomyśl o użyciu silni. W przypadku 3 słów istnieje \(3!\) (3 silnia) uporządkowań. Dla 5 słów istnieje \(5!\) uporządkowań. Spójrz na wyjaśnienie poniżej, jeśli nie wiesz, czym jest silnia, lub jeśli zapomniałeś!
-
Co to znaczy?. Silnie
Silnie są bardzo łatwe do obliczenia; po prostu pomnóż wszystkie liczby całkowite od danej liczby w dół do 1. Na przykład, aby obliczyć \(5!\), po prostu mnożysz: 5 x 4 x 3 x 2 x 1 = 120. Dla \(8!\) po prostu mnożysz 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40 320.
Jak wspomniano powyżej, silnia liczby określa, ile permutacji (uporządkowań) byłoby dla tej liczby słów (zakładając, że wszystkie są różne). Oznacza to, że jeśli układasz 8 słów, będzie 40 320 sposobów ich ułożenia (dlatego nie prosiliśmy o wypróbowanie tego w pierwszym ćwiczeniu!!)
Twój kalkulator może mieć przycisk ,,!'' do obliczania silni, a arkusze kalkulacyjne mają zwykle funkcję ,,FACT'', chociaż w przypadku silni poniżej 10 w tym rozdziale, zalecamy obliczyć je ,,na piechotę'', a następnie użyć kalkulatora do sprawdzenia. Zrozumienie sposobu obliczania silni jest niezbędne do zrozumienia reszty tego rozdziału!
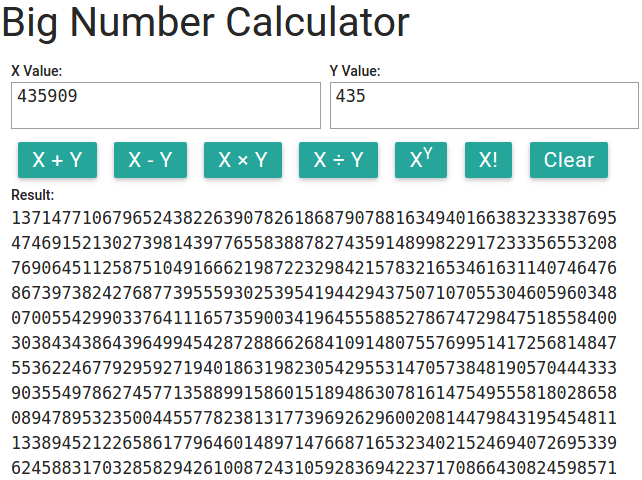
W przypadku silni większych liczb większość kalkulatorów nie działa zbyt dobrze; na przykład 100! ma 158 cyfr. Możesz użyć poniższego kalkulatora do pracy z dużymi liczbami (szczególnie podczas korzystania z silni i wykładników).
Spróbuj obliczyć 100! za pomocą tego kalkulatora -- jest to liczba różnych tras, którymi sprzedawca podróżujący może odwiedzić 100 miejsc (nie licząc miejsca startowego). Za pomocą tego kalkulatora możesz skopiować i wkleić wynik z powrotem do wejścia, jeśli chcesz wykonać dalsze obliczenia na tej liczbie. Jeśli wykonujesz te obliczenia jako zadanie, powinieneś również skopiować każdy krok obliczeń do swojego rozwiązania, aby pokazać, w jaki sposób uzyskałeś wynik.
W Internecie dostępne są inne kalkulatory dużych liczb; na przykład Big Integer Calculator. Można też znaleźć w Internecie wersje do ściągnięcia na komputer lub smartfona.
Jako ostatnie ćwiczenie dotyczące sortowania przez permutacje, oblicz, ile czasu zajmie komputerowi sortowanie 100 liczb przy użyciu sortowania przez permutacje. Pamiętaj, że możesz użyć powyższego kalkulatora. Załóżmy, że nie musisz się martwić, ile czasu zajmie wygenerowanie permutacji, tylko ile czasu zajmie ich sprawdzenie. Załóżmy, że masz komputer, który tworzy i sprawdza jedno uporządkowanie co nanosekundę.
- Ile uporządkowań należy sprawdzić przy sortowaniu 100 liczb?
- Ile uporządkowań można sprawdzić w ciągu sekundy?
- Ile uporządkowań można sprawdzić w ciągu roku?
- Ile lat zajmie sprawdzenie wszystkich uporządkowań?
-
Dla nauczyciela. Rozwiązanie
Liczba uporządkowań 100 liczb to 100!, czyli 93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000.
Nanosekunda to 1/1 000 000 000 sekundy, więc założony system może sprawdzić miliard uporządkowań na sekundę.
Mamy 60x60x24x365 sekund w roku nieprzestępnym, czyli 31 536 000, więc założony system może sprawdzić 31 536 000 miliardów uporządkowań w ciągu roku, a więc dzieląc 100! przez tą liczbę otrzymujemy 2 959 354 878 359 467 043 432 877 944 452 901 461 527 015 736 440 310 168 334 378 611 593 658 041 388 569 114 946 139 776 006 992 588 985 721 014 739 574 573 764 941 185 024 000 000 000 000 lat. To niewyobrażalna ilość czasu, żeby posortować 100 liczb. Ten algorytm naprawdę nie jest efektywny!
A w ramach ciekawostki, zrób kilka obliczeń na podstawie poniższych założeń. Ile czasu zajmie użycie sortowania przez permutacje na 100 liczbach? Co stanie się najpierw: algorytm się zakończy, czy wszechświat się skończy?
- We wszechświecie jest \(10^{82}\) atomów.
- Wszechświat będzie trwał kolejne 14 miliardów lat, zanim się skończy.
- Załóżmy, że każdy atom we wszechświecie to komputer, który może sprawdzić jedno uporządkowanie co nanosekundę.
-
Dla nauczyciela. Rozwiązanie
W powyższym przykładzie wszechświat zakończyłby się przed posortowaniem 100 liczb!
Powinniście już być w pełni świadomi tego, co się dzieje. Sortowanie przez permutacje jest tak nieefektywne, że sortowanie nim 100 liczb zajęłoby tyle czasu, że jest w zasadzie niemożliwe. Próba użycia sortowania przez permutacje do nietrywialnej liczby elementów po prostu nie zadziała. Chociaż sortowanie przez wstawianie jest dużo wolniejsze niż sortowanie szybkie czy sortowanie przez scalanie, nie byłoby niemożliwe, by Facebook użył sortowania przez wybór, aby posortować listę 1 miliarda użytkowników. Zajęłoby to o wiele więcej czasu niż sortowanie szybkie, ale byłoby to wykonalne. Jednak użycie sortowania przez permutacje byłoby niemożliwe!
Musimy teraz rozróżnić algorytmy, które są w praktyce użyteczne, i algorytmy, które będą potrzebowały miliardów lat, aby zakończyć działanie, nawet przy niewielkich ilościach danych wejściowych, takich jak 100 elementów.
Informatycy mówią, że algorytm jest praktycznie niewykonalny, jeśli jego działanie przy danych wejściowych o rozsądnej wielkości zajmie całkowicie nierozsądną ilość czasu. Sortowanie przez permutacje jest dobrym przykładem algorytmu który jest praktycznie niewykonalny. Pojęcie ,,praktycznie niewykonalny'' jest nieco bardziej formalnie używane w informatyce; wyjaśniono to w następnym podrozdziale.
Ale sam problem sortowania elementów nie jest trudny do rozwiązania -- mimo że algorytm sortowania przez permutacje nie jest praktycznie wykonalny, istnieje wiele innych wydajnych i mniej wydajnych algorytmów, które można wykorzystać do rozwiązania problemu sortowania w rozsądnym czasie: sortowanie szybkie (ang. Quicksort), sortowanie przez scalanie (ang. mergesort), sortowanie przez wybór, a nawet sortowanie bąbelkowe! Istnieją jednak pewne problemy, dla których JEDYNE znane algorytmy są praktycznie niewykonalne. Problemy tej kategorii są znane jako problemy trudne.
-
Ciekawostka. Wieże Hanoi
Problem wież Hanoi jest łamigłówką, w której masz stos krążków o rosnącej od góry do dołu wielkości na jednym słupku i dwa puste słupki. Zadanie polega na przeniesieniu wszystkich krążków z jednego słupka na drugi, ale bez kładzenia większego krążka na mniejszym. Jest opisany w Wikipedii.
Ten problem nie może zostać rozwiązany w mniej niż \(2^{n-1}\) ruchach, więc jest praktycznie niewykonalny (program komputerowy, który wylicza wszystkie ruchy, użyłby co najmniej \(2^{n-1}\) kroków). W przypadku 6 krążków potrzeba tylko 63 ruchów, ale w przypadku 50 krążków będzie to 1 125 989 906 832 623 ruchów.
Zwykle mówimy o takim problemie, że ma złożoność \(2^n\), ponieważ odejmowanie jedynki, by otrzymać wartość dokładną, prawie nie robi różnicy, a krótsze wyrażenie jest łatwiejsze w komunikacji.
Wieże Hanoi to jeden z problemów, o którym wiemy na pewno, że rozwiązanie zajmuje czas wykładniczy. Istnieje wiele trudnych problemów, w których tak nie jest -- nie mamy dla nich praktycznie wykonalnych rozwiązań, ale nie wiemy na pewno, że nie istnieją. Poza tym nie jest to prawdziwy problem -- to tylko gra (chociaż na jej podstawie stworzono system kopii zapasowych). Jest to jednak dobry przykład algorytmu czasu wykładniczego, w którym dodanie jednego dysku podwoi liczbę kroków wymaganych do wytworzenia rozwiązania.
-
Dla nauczyciela. Praca z dużymi liczbami
Następny podrozdział wymaga od uczniów użycia aplikacji do eksperymentów z obliczeniami na ogromnych liczbach, które napotkają w praktycznie niewykonalnych algorytmach. Najlepiej to ćwiczenie przeprowadzić w klasie, tak by uczniowie mieli wsparcie przy obliczeniach na dużych liczbach. Dobrze by było, gdyby zdali sobie sprawę, jak niepraktyczny byłby program potrzebujący do znalezienia rozwiązanie w ciągu milionów lat: nawet gdyby pojawił się 1000 razy szybszy komputer, ukończenie go i tak zajęłoby 1000 lat. Niektóre z czasów, które pojawiają się poniżej, są tak długie, że przekraczają nasze wyobrażenie i najlepiej pokazać jak są nieprzydatne nawet przy użyciu komputera o tysiąc, milion, a nawet miliard razy większej mocy obliczeniowej.
Wcześniejsza wersja tego rozdziału zawierała poniższy arkusz kalkulacyjny do wykonywania obliczeń na wielkich liczbach; zachowaliśmy odnośnik, choć nowa aplikacja radzi sobie znacznie lepiej z dużymi liczbami w obliczeniach. Jeśli jesteś zainteresowany, możesz pobrać arkusz kalkulacyjny.
Istnieje bardzo prosta zasada, którą kierują się informatycy, aby zdecydować, czy algorytm jest praktycznie wykonalny czy nie, na podstawie złożoności (szacowanej liczby kroków) algorytmu. W uproszczeniu, jeśli czas który zajmuje algorytm jest wykładniczy lub dłuższy, dla danych wejściowych o rozmiarze n, to jest oznaczony jako praktycznie niewykonalny. Ta prosta zasada jest nieco zgrubna, ale jest szeroko stosowana i dostarcza użytecznych wskazówek. (Jak wiadomo, złożoność n! jest większa niż funkcja wykładnicza).
Aby zobaczyć, co to oznacza, zastanówmy się, jak długo mogą działać różne algorytmy. Poniższa aplikacja wykona za ciebie obliczenia, aby oszacować czas działania algorytmu. Możesz wybrać, czy czas działania jest wykładniczy (to znaczy \(2^n\), czyli czas wymagany dla problemu wież Hanoi o n krążkach) lub silniowy (to znaczy \(n!\), czyli czas potrzebny na sprawdzenie wszystkich możliwych tras, którymi komiwojażer może odwiedzić n miast innych niż punkt początkowy). Możesz użyć aplikacji poniżej, aby obliczyć czas.
Na przykład wybierz czas n! dla TSP i wpisz 20 dla wartości n (to jest sprawdzenie wszystkich możliwych wizyt komiwojażera w 20 miastach). Naciśnij klawisz ENTER albo TAB, aby zaktualizować obliczenia. Kalkulator pokaże dużą liczbę sekund, które program będzie potrzebował do wykonania; możesz zmienić jednostki na lata, aby zobaczyć, jak długo by to potrwało.
-
Dla nauczyciela. Rozwiązanie
Przy początkowych ustawieniach w aplikacji, TSP dla 20 miast zajmie 2 432 902 008 176 640 000,00 sekund, co stanowi 773 056 638,51 wieków (zwróć uwagę, że kalkulator musi być ustawiony na n!, aby użyć go do TSP). Notabene podajemy bardzo dokładne liczby, aby sprawdzić, czy masz dobry wynik; w praktyce szacunek jest bardzo zgrubny, a zamiast 773 056 638,51 stuleci, równie trafne jest powiedzenie ,,około 770 milionów wieków'', a nawet tylko ,,setki milionów stuleci''. Przedstawienie tego w geologicznych ramach czasowych może lepiej to przybliżyć uczniom.
Do tej pory obliczenia zakładały, że komputer wykona tylko 1 operację na sekundę; spróbuj przejść do miliona (1 000 000) operacji na sekundę, co jest bardziej realistyczne i sprawdź, ile czasu zajmie.
-
Dla nauczyciela. Rozwiązanie
Gdy komputer jest milion razy szybszy, czas dla TSP w 20 miastach zmniejsza się z 773 056 383,51 wieków do 733,06 wieków. To wciąż zupełnie niepraktyczne!
Innym sposobem na szybsze rozwiązywanie problemów jest jednoczesna praca wielu procesorów nad różnymi rozwiązaniami. Jeśli miałbyś kupić 1000 procesorów (na przykład 1000 komputerów lub 250 czterordzeniowych komputerów) i każdy z nich przetestowałby różne trasy, to rozwiązanie można by było znaleźć 1000 razy szybciej. Spróbuj zmienić liczbę procesorów na 1000 i zobacz, ile czasu to zajmie (może się okazać, że trzeba zmienić jednostki z powrotem -- czy będą to sekundy? godziny? dni?)
-
Dla nauczyciela. Rozwiązanie
1000 procesorów skraca czas pracy do 77,31 lat. To wciąż niepraktycznie duża moc obliczeniowa, ale zaczynamy docierać do obszaru, w którym rozwiązanie problemu nie jest całkowicie niemożliwe.
Powyższa aplikacja szacuje czas działania różnych algorytmów, przetwarzających n elementów. Załóżmy, że mamy bardzo szybki komputer. Załóż, że komputer może wykonać milion milionów (1 000 000 000 000) kroków na sekundę. Czy to jest osiągalne? A co się stanie, jeśli dodasz choćby dwa miasta do problemu (n = 22 zamiast n = 20)?
-
Dla nauczyciela. Rozwiązanie
Ta niesamowicie duża szybkość skróciłaby czas do 40,55 sekundy. Jednak zwiększenie problemu do zaledwie 22 miast powoduje ponowny rozrost do 13,01 dni. Najważniejsze jest to, że nawet jeśli masz szybką sieć komputerów, która może rozwiązać konkretny problem, dodanie zaledwie kilku elementów do problemu spowoduje, że ponownie znajdzie się on poza zasięgiem.
Rozważmy teraz algorytm, który ma złożoność \(n^2\) (wiele algorytmów wykonuje w przybliżeniu tę liczbę kroków, w tym sortowanie, o którym wspomniano wcześniej). Wpisz wartość 1 000 000 dla n, aby sprawdzić, ile czasu zajmie sortowanie miliona elementów na jednym procesorze (ustaw liczbę kroków na sekundę na 1 000 000 000 000, ale ustaw liczbę procesorów na 1) -- powinien pokazać, że zajmie to około 1 sekundy na naszej hipotetycznej, bardzo szybkiej maszynie. Teraz wpisz 10 milionów dla n -- chociaż algorytm sortuje listę 10 razy większą, zajmuje to ponad 10 razy dłużej i zajmuje teraz już minuty, a nie sekundy. Przy jakiej wartości n czekanie na wynik przestaje wchodzić w rachubę -- to znaczy, jak duży musiałby być problem, aby zajmował lata? Czy ktokolwiek, kiedykolwiek będzie sortował tak wiele elementów -- na przykład przy sortowaniu nazwisk wszystkich osób na świecie albo wszystkich par zasad w ludzkim genomie?
-
Dla nauczyciela. Rozwiązanie
Wykonanie algorytmu o złożoności \(n^2\) z 10 milionami elementów zajmuje 100 sekund (za każdym razem, gdy n mnożone jest przez 10, zajmie 100 razy dłużej).
Gdy n wynosi tysiąc milionów, zajmuje to prawie 12 dni i w tym miejscu możesz uznać, że już nie wchodzi to w grę. Przy \(n=10 000 000 000\) zajmuje to około 3,18 lat, czyli prawdopodobnie dłużej niż komputer może działać bez przerwy. Ale to dość duża liczba elementów do przetworzenia -- na przykład wystarczająco duża, by poradzić sobie z populacją całego świata. Istnieje również możliwość poprawy czasu działania dzięki zastosowaniu rozsądnej liczby procesorów.
A co z algorytmem o złożoności \(n^3\)? Jaki jest największy zestaw danych wejściowych, który można przetwarzać w rozsądnym czasie?
-
Dla nauczyciela. Rozwiązanie
Algorytm o złożoności \(n^3\) może przetworzyć 1 000 000 elementów w 11,57 dni (nadal zakładamy, że wykonywane jest \(10^{12}\) operacji na sekundę). Milion jest niczym w porównaniu do populacji świata, a nawet wielu krajów, ale wiele prawdziwych problemów jest mniejszych.
Teraz spróbuj zrobić to samo, gdy liczba kroków wynosi \(2^n\), ale zacznij od wartości 10 dla n, a następnie spróbuj 30, 40, 50 i tak dalej. Prawdopodobnie okaże się, że dla wejścia około 70 pozycji wykonanie algorytmu zajmie zbyt dużo czasu. Czy jest o wiele gorzej w przypadku 80 przedmiotów?
-
Dla nauczyciela. Rozwiązanie
Algorytm o złożoności \(2^n\) jest w zupełnie innej klasie niż poprzednie. Wykonanie go dla 10 elementów zajmuje ułamek sekundy (dokładnie 1,02 nanosekundy), a dla 60 elementów zajmuje 13,34 dni, ale już zaledwie 70 elementów powoduje wzrost do 37,51 lat, zaś dla 80 elementów zajmuje to 384 wieki. Niewielkie wzrosty liczby przedmiotów skutkują OGROMNYM wzrostem czasu potrzebnego do ich przetworzenia.
Teraz zwiększ liczbę operacji na sekundę do 10 razy większej. Czy to pomaga rozwiązać większe problemy?
-
Dla nauczyciela. Rozwiązanie
Liczenie 10 razy szybciej zredukuje 384 stulecia do 38,4 stulecia -- znacznie szybciej, ale wciąż jest to niemożliwie duża ilość czasu. Płynie stąd nauka, że algorytm będzie tak powolny, że nawet ogromna poprawa wydajności sprzętu nie będzie miała większego wpływu.
Wypróbowując te liczby, najprawdopodobniej natrafisz na barierę między problemami ,,praktycznie wykonalnymi'' i ,,praktycznie niewykonalnymi''. Algorytmy, które potrzebują \(n^2\), \(n^3\) lub nawet \(n^4\) kroków, aby rozwiązać problem (taki jak sortowanie listy), nie są może wspaniałe, ale z wystarczająco szybkim komputerem i przy wielkości danych wejściowych problemów, które napotykamy w typowych zastosowaniach, mamy szansę doczekać się wyniku w ciągu ludzkiego życia. Są one traktowane jako praktycznie wykonalne. Jednak w przypadku algorytmów, które zajmują \(2^n\), \(3^n\) lub więcej kroków, wymagany czas działania może przekroczyć miliardy lat nawet dla małej wielkości danych wejściowych, a używanie tysięcy razy szybszych komputerów nadal nie pomaga rozwiązać większych problemów. Takie problemy są uważane za praktycznie niewykonalne. Matematycznie, granica między praktycznie wykonalnymi i praktycznie niewykonalnymi problemami przebiega między wielomianową liczbą kroków (wielomiany to na przykład \(n^2\), \(n^3\), \(n^4\) i tak dalej), a wykładniczą liczbą kroków (\(2^n\), \(3^n\), \(4^n\), i tak dalej).
Oba wzory \(n^2\) i \(2^n\) wyglądają bardzo podobnie, ale są naprawdę bardzo odmienne i mogą oznaczać różnicę między kilkoma sekundami a wieloma tysiącleciami czasu działania programu. Celem tego rozdziału jest rozwinięcie świadomości, że istnieje wiele problemów, dla których mamy algorytmy praktycznie wykonalne, ale jest też wiele takich, dla których nie znaleźliśmy żadnych algorytmów praktycznie wykonalnych. Wiedza o tym jest bardzo ważna, bo bezowocne będzie pisanie programów, które nie są praktycznie wykonalne, chyba że ma się zamiar przetwarzać tylko bardzo niewiele danych wejściowych.
Zauważ, że algorytmy, które potrzebują silniowej ilości czasu (\(n! = 1 \cdot 2 \cdot 3 \cdot \ldots n\)) też należą do kategorii praktycznie niewykonalnych (w rzeczywistości potrzebują dużo więcej czasu niż \(2^n\)).
W zasadzie każdy algorytm, który próbuje wszystkich kombinacji danych wejściowych, na pewno nie będzie praktycznie wykonalny, ponieważ liczba kombinacji będzie prawdopodobnie wykładnicza lub silniowa. Dlatego warto mieć na uwadze, że projektowanie algorytmu, który po prostu wypróbowuje wszystkie możliwe rozwiązania, aby zobaczyć, które jest najlepsze -- zazwyczaj nie zadziała.
Chociaż podaliśmy \(n^6\) jako przykład czasu w praktyce obliczalnego, prawie wszystkie algorytmy, z którymi się spotkasz, mają złożoność \(n^3\) i mniej, lub \(2^n\) i więcej -- tylko te bardzo wyspecjalizowane wchodzą w lukę między nimi. Istnieje więc duża przepaść między praktycznie wykonalnymi i praktycznie niewykonalnymi problemami, a zmaganie się z nią to jeden z największych problemów w informatyce!
Co z prawem Moore'a, które mówi, że moc obliczeniowa komputerów rośnie wykładniczo? Może oznacza to, że jeśli trochę zaczekamy, komputery będą w stanie rozwiązać problemy, które są obecnie trudne do rozwiązania? Niestety to rozumowanie jest błędne; praktycznie niewykonalne problemy mają również charakter wykładniczy, a więc tempo poprawy wynikające z prawa Moore'a pozwoli tylko na rozwiązanie nieco większych problemów. Załóżmy na przykład, że szybkość obliczeniowa podwaja się co 18 miesięcy (optymistyczna interpretacja prawa Moore'a), a mamy nierozwiązywalny problem, który wymaga \(2^n\) kroków (a wiele wymaga więcej), to za 18 miesięcy będziemy w stanie rozwiązać problem, który jest tylko o jeden element większy. Na przykład, jeśli potrafisz rozwiązać ten problem dla 50 przedmiotów (50 krajów na mapie do pokolorowania, 50 miast odwiedzanych przez komiwojażera, czy 50 krążków w problemie wież Hanoi) w ciągu 24 godzin, to za 18 miesięcy można oczekiwać, że kupisz komputer, który w najlepszym razie rozwiąże problem z 51 przedmiotami! Za 20 lat najprawdopodobniej będziesz w stanie zdobyć komputer, który rozwiąże problem z 55 przedmiotami w ciągu jednego dnia. Musiałbyś być bardzo cierpliwy, by prawo Moore'a tutaj pomogło -- musisz być gotów czekać dziesięciolecia na drobną poprawę!
Przypominamy, że jeśli chcesz wykonywać obliczenia na wielkich liczbach, możesz użyć kalkulatora:
Przykładem bardzo trudnego problemu jest problem komiwojażera (TSP). W TSP mamy wiele lokalizacji (miast, domów, lotnisk, itp.) i można podróżować między dowolną parą lokalizacji. Celem jest znalezienie najkrótszej trasy, która przejdzie przez wszystkie lokalizacje -- robi to aplikacja na początku tego rozdziału.
Naukowcy spędzili wiele czasu, próbując znaleźć skuteczne rozwiązania problemu komiwojażera, ale nie byli w stanie znaleźć praktycznie wykonalnego algorytmu, który by go rozwiązywał. Nauczyliście się w poprzednim podrozdziale, że algorytmy praktycznie niewykonalne są bardzo powolne, do tego stopnia, że nie można ich użyć. Ponieważ jedyne rozwiązania TSP są praktycznie niewykonalne, TSP jest znany jako problem trudny obliczeniowo.
Nie zostało udowodnione, że nie jest możliwe znalezienie praktycznie wykonalnego rozwiązania TSP, chociaż wielu czołowych informatyków na świecie pracowało nad tym problemem przez ostatnie kilkadziesiąt lat, próbując bez powodzenia znaleźć rozwiązanie. Za to udało im się znaleźć tysiące innych problemów, które są również obliczeniowo trudne, a co ważniejsze, jeśli znajdzie się rozwiązanie dla któregokolwiek z tych problemów, wiemy, jak zmienić je na rozwiązanie dla każdego z pozostałych (są to tak zwane problemy NP-zupełne). Jeden za wszystkich, wszyscy za jednego -- łącznie z problemem TSP. Więc nie będzie zwykłym lenistwem, jeśli poddasz się przed znalezieniem optymalnego algorytmu TSP -- próbowano od dziesięcioleci i nikt nie znalazł algorytmu, który byłby praktycznie wykonalny. Oczywiście jest to również silna motywacja, aby spróbować go znaleźć -- jeśli to zrobisz, rozwiążesz tysiące innych problemów za jednym zamachem! Dla naukowca praca nad tym jest wspaniała, ale jeśli masz napisać taki program do końca miesiąca, lepiej nie stawiać na to, że się uda.
Próba znalezienia rozwiązania TSP polegająca na wypróbowaniu wszystkich możliwych ścieżek na mapie (jak w aplikacji z początku tego rozdziału) nie jest praktycznym podejściem, bo liczba możliwych ścieżek wymyka się spod kontroli. W zaproponowanym w tym podrozdziale projekcie będziesz oceniał, ile czasu by to zajęło.
Choć TSP został pierwotnie przedstawiony jako problem, z którym spotykają się handlowcy, gdy jeżdżą do kilku różnych miejsc i chcą je odwiedzić w kolejności, która daje najkrótszą trasę (mniejsze zużycie paliwa), ten sam problem dotyczy również wielu innych sytuacji. Firmy kurierskie i dostawcze mają różne warianty tego problemu -- często z dodatkowymi ograniczeniami, takimi jak ograniczenie czasu pracy kierowcy lub możliwość wykonywania skrętów w prawo szybciej niż w lewo.
-
Dla nauczyciela. Więcej informacji na temat TSP
Istnieje obszerna strona internetowa w języku angielskim o aktualnym stanie wiedzy na temat TSP: http://www.tsp.gatech.edu/. Obejmuje ona także gry i informacje o bieżącym największym rozwiązanym problemie komiwojażera (którego rozwiązanie zazwyczaj zajmuje miesiące lub lata na bardzo wydajnych komputerach).
Ponieważ problemy te są ważne dla prawdziwych firm, nie należy po prostu rezygnować i mówić, że nie ma rozwiązania. Zamiast tego, w konfrontacji z trudnym problemem, informatycy szukają algorytmów, które dają przybliżone rozwiązania -- rozwiązania, które nie są idealnie poprawne czy optymalne, ale są na tyle bliskie, że są użyteczne. Osłabiając wymaganie, że rozwiązanie musi być całkowicie poprawne, często można wymyślić algorytmy, które znajdą wystarczająco dobre rozwiązania w rozsądnym czasie. Ten rodzaj algorytmu nazywa się heurystycznym -- wykorzystuje zasady, sugerujące dobre wybory i budujące rozwiązanie na bazie dokonywania niezłych wyborów.
Prosta heurystyka, która często działa dobrze, to zachłanny algorytm heurystyczny -- algorytm, który po prostu dokonuje wyboru, który wygląda na najlepszy na każdym etapie. Na przykład dla TSP zachłanny algorytm heurystyczny może zawsze przechodzić do najbliższego miasta. Nie zawsze będzie to najlepszy wybór, ale jest bardzo szybki, a doświadczenie pokazuje, że zazwyczaj jest mniej niż o 25% gorszy od optymalnego. Istnieją bardziej wyrafinowane sposoby projektowania przybliżonych algorytmów, które mogą działać lepiej niż on (niektóre są tylko o 3% gorsze od optymalnego rozwiązania TSP), ale trwają dłużej.
Istnieją firmy zajmujące się oprogramowaniem, które starają się tworzyć coraz lepsze przybliżone algorytmy do kierowania pojazdami dostawczymi przez GPS. Firmy, które piszą lepsze algorytmy, mogą drogo sprzedawać swoje programy, jeśli ich trasy są szybsze, ze względu na możliwe do uzyskania oszczędności paliwa i czasu.
Ciekawą rzeczą, z którą trudno się pogodzić, jest to, że można napotkać dwa bardzo podobne problemy, z których jeden jest trudny, a drugi jest łatwy. Na przykład, znalezienie najkrótszej trasy między dwoma punktami (jak to zwykle robi urządzenie GPS) jest problemem łatwym do pokonania, jednak znalezienie najkrótszej trasy przez wiele punktów (TSP) -- nie jest. Nawiasem mówiąc, znalezienie najdłuższej ścieżki między dwoma punktami (bez przechodzenia przez jakikolwiek fragment trasy dwa razy) jest również trudne, nawet pomimo tego, że znalezienie najkrótszej ścieżki jest łatwe!
-
Dla nauczyciela. Problem pułapek na raki
Ten projekt opiera się na takiej historii. Pewien rybak łowiący raki, umieścił w wodzie około 18 pułapek. Każdego dnia rybak odwiedza łodzią wszystkie pułapki i sprawdza, czy nie złapały się w nią raki.
Rybak zaczął się zastanawiać, jaka jest najkrótsza droga, by sprawdzić wszystkie pułapki i poprosił cię o pomoc. Ponieważ co kilka tygodni pułapki trzeba przenieść, rybak wolałby poznać ogólny sposób rozwiązania problemu, niż rozwiązanie pojedynczego układu pułapek. W związku z tym twoje badania muszą uwzględniać więcej niż jeden możliwy układ pułapek, a badane układy powinny mieć pułapki rozmieszczone przypadkowo tj. nie w liniach, wzorach lub figurach geometrycznych.
Gdy zostaniesz poproszony o wygenerowanie losowej mapy pułapek, weź garść tylu monet (lub żetonów) ile jest pułapek i rzuć je na kartkę papieru A4. Jeśli któreś wylądują na sobie, umieść je obok siebie tak, aby się dotykały, ale nie zachodziły na siebie. Podnieś monety jedną po drugiej, robiąc kropkę na papierze w środku miejsca na którym leżała moneta. Ponumeruj kropki. Każda kropka przedstawia jedną pułapkę, którą musi sprawdzić rybak. Powinieneś oznaczyć lewy górny róg kartki jako przystań dla łodzi, z której wypływa rybak.
Wygeneruj mapę z 7 lub 8 pułapkami, używając opisanej powyżej metody generowania map losowych. Zrób dodatkową kopię tej mapy, ponieważ będziesz jej później potrzebować.
Korzystając z intuicji, znajdź najkrótszą drogę między pułapkami.
Teraz wygeneruj mapę (tą samą metodą co powyżej) z 15 -- 25 pułapkami. Zrób więcej niż jedną kopię tej mapy, ponieważ będziesz potrzebować jej później.
Teraz na tej nowej mapie spróbuj użyć swojej intuicji, aby znaleźć najkrótszą ścieżkę pomiędzy pułapkami. Nie trać więcej niż 5 minut na to zadanie; nie musisz wpisywać rozwiązania w zadaniu domowym. Dlaczego to zadanie było bardzo trudne? Czy możesz mieć pewność, że znalazłeś optymalne rozwiązanie?
Jeśli pułapki nie ułożyły się w okrąg lub owal, prawdopodobnie znalezienie najkrótszej trasy było bardzo trudne. Komputer miałby jeszcze więcej trudności, bo nie może skorzystać z wizualnego wyszukiwania ani intuicji, aby ułatwić sobie zadanie. Komputer może brać pod uwagę tylko dwa miejsca naraz, podczas gdy ty możesz spojrzeć na więcej niż dwa. Ale nawet dla ciebie problem byłby trudny! Nawet jeśli zmierzysz odległość między każdą parą miejsc i narysujesz linie między nimi, i narysujesz je na mapie, tak żeby nie musieć oceniać odległości między nimi na oko, to nadal będzie to dla ciebie trudne zadanie!
Prostym algorytmem gwarantującym odnalezienie najkrótszej trasy jest sprawdzenie wszystkich możliwych tras. Obejmuje to ustalenie jakie są wszystkie możliwe trasy, a następnie sprawdzenie każdej z nich. Każda trasa może być zapisana jako lista miejsc (tj. numerów pułapek), w takim porządku w jakim trzeba je przejść. To powinno brzmieć znajomo, jeśli zrobiłeś sortowanie przez permutacje omówione wcześniej. Zupełnie jak w tamtym zadaniu, w którym wymieniłeś wszystkie możliwe uporządkowania liczb, algorytm ten wymagałby wyszczególnienia wszystkich możliwych uporządkowań pułapek (chociaż nie musisz wymieniać wszystkich uporządkowań w tym projekcie!).
Ile jest możliwych tras dla większego z generowanych przez ciebie przykładów? W jaki sposób wiąże się to z sortowaniem przez permutacje i silnią? Ile czasu zajęłoby obliczenie najkrótszej trasy na mapie, zakładając, że komputer może sprawdzić 1 miliard (1 000 000 000) możliwych tras na sekundę (tzn. może sprawdzić jedną trasę w ciągu nanosekundy)? Jakie wnioski można wyciągnąć na temat kosztu tego algorytmu? Czy byłby to dobry sposób, aby rybak zdecydował, którą drogę wybrać?
Upewnij się, że wypisałeś wszystkie działania matematyczne, jakie wykonałeś w odpowiedzi na powyższe pytania!
Tak więc ten algorytm nie jest praktycznie wykonalny, ale być może istnieje bardziej sprytny algorytm, który jest praktycznie wykonalny? Odpowiedź brzmi: nie wiadomo.
Powinieneś być w stanie stwierdzić, że ten problem jest równoważny z TSP, a zatem jest problemem trudnym. Skąd możesz to wiedzieć? Co jest odpowiednikiem miasta w tym scenariuszu? Co jest odpowiednikiem drogi?
Ponieważ wiemy, że problem pułapek na raki jest przykładem TSP, i że nie jest znany żaden praktycznie wykonalny algorytm dla TSP, wiemy, że na razie nie ma również algorytmu praktycznie wykonalnego dla problemu pułapek na raki. Chociaż istnieją nieco lepsze algorytmy niż te, które wykorzystaliśmy powyżej, wciąż nie są one praktycznie wykonalne i przy wystarczającej liczbie pułapek niemożliwe byłoby opracowanie nowej trasy, zanim rybak znowu będzie musiał przesunąć pułapki!
Zamiast tracić czas na wymyślanie sprytnego algorytmu, którego jak dotąd nikt nie był w stanie znaleźć, musimy polegać na algorytmie, który wygeneruje przybliżone rozwiązanie. Rybak byłby zadowolony z przybliżonego rozwiązania, które jest wprawdzie na przykład o 10% dłuższe niż najlepsza z możliwych tras, ale które komputer jest w stanie szybko znaleźć.
Istnieje kilka sposobów podejścia do tego problemu. Niektóre z nich są lepsze od innych, a niektóre są lepsze od innych przy niektórych układach pułapek. Jednym z bardziej oczywistych przybliżonych algorytmów jest rozpoczęcie od doku łodzi w lewym górnym rogu mapy i przejście do najbliższej pułapki. Stamtąd powinieneś udać się do najbliższej pułapki z tej pułapki i wielokrotnie udawać się do najbliższej pułapki, która nie została jeszcze sprawdzona. Takie podejście jest znane jako zachłanny algorytm heurystyczny, ponieważ zawsze dokonuje wyboru, który wydaje się w danym momencie najlepszy, zamiast podjąć nieco gorszą decyzję, żeby później uzyskać dzięki temu lepszy wynik. Zrozumiesz, dlaczego niekoniecznie prowadzi to do optymalnego rozwiązania po wykonaniu następujących ćwiczeń.
Na kopii obu twoich wygenerowanych map narysuj linie pomiędzy pułapkami, aby pokazać trasę, którą znajdziesz dzięki algorytmowi zachłannemu (powinieneś był zrobić więcej niż jedną kopię każdej z map!).
W przypadku mapy z mniejszą liczbą pułapek (7 lub 8) porównaj optymalne rozwiązanie i rozwiązanie przybliżone. Czy są one takie same? Czy będą w każdym przypadku takie same? Narysuj mapę, na której byłyby inne (możesz wybrać miejsca, w których umieścisz pułapki, po prostu użyj tylu pułapek, ile tylko ci trzeba, żeby to pokazać).
Na większej mapie pokaż, że nie masz optymalnego rozwiązania. Najlepszym sposobem jest pokazanie trasy podobnej do twojej, ale krótszej. Krótsze rozwiązanie, które znajdziesz, nie musi być optymalnym rozwiązaniem, tylko musi być krótsze od tego, które znalazł algorytm zachłanny (porozmawiaj z nauczycielem, jeśli nie możesz znaleźć krótszej trasy, a on doradzi, czy nie powinieneś stworzyć nowej mapy). Będziesz musiał pokazać mapę z trasą zachłanną i również zaznaczoną krótszą od niej trasą. Wyjaśnij technikę, której użyłeś do pokazania, że istniało krótsze rozwiązanie. Pamiętaj, że nie ma znaczenia, o ile krótsze jest nowe rozwiązanie, o ile jest ono choć trochę krótsze niż rozwiązanie przybliżone -- dzięki temu pokazujesz, że przybliżone rozwiązanie nie może być optymalne.
Chociaż zachłanny algorytm generuje jedynie przybliżone rozwiązanie, a nie optymalne, wyjaśnij, dlaczego jest on bardziej odpowiedni dla rybaka, niż szukanie optymalnego rozwiązania.
Dlaczego ważne jest, aby rybak znalazł krótką drogę pomiędzy pułapkami, a nie tylko odwiedzał je w przypadkowej kolejności? Poszukaj innych problemów, które są równoważne z TSP, które firmy z całego świata napotykają na co dzień. Dlaczego dla tych firm ważne jest znalezienie dobrych rozwiązań dla TSP? Oszacuj, ile pieniędzy firma kurierska mogłaby marnować przez rok, gdyby ich trasy dostaw były o 10% gorsze od optymalnych. Jak wiele różnych lokalizacji / miejscowości / itd. ich rozwiązania TSP muszą być w stanie przetworzyć?
Znajdź układ pułapek, który powoduje, że zachłanny algorytm znajdzie bardzo nieefektywną trasę. Dlaczego jest ona nieefektywna? Nie martw się o znalezienie najgorszego przypadku, wystarczy znaleźć przypadek, który wydaje się być naprawdę zły. Jaki jest ogólny układ pułapek, który powoduje, że ten zachłanny algorytm jest nieefektywny?
Nie zapomnij umieścić w swoim raporcie wprowadzającego akapitu, który przedstawia najważniejsze idee. Powinien zawierać krótki opis tego, co to jest problem praktycznie niewykonalny i jak informatyk radzi sobie z takim problemem. W raporcie powinieneś również własnymi słowami opisać problem komiwojażera i problem rybaka. Wyjaśnij, dlaczego problem rybaka jest realistycznym problemem, który może mieć dla kogoś znaczenie.
-
Dla nauczyciela. W trakcie budowy
O wielu ciekawych trudnych problemach nie wspomnieliśmy w tym rozdziale, ale poniżej podajemy kilka alternatyw dla problemu TSP, które mogą być wykorzystane do rozważań nad praktyczną wykonalnością, jeśli masz uczniów, którzy mogą pracować nad tym samodzielnie.
Istnieją tysiące problemów, takich jak TSP, dla których nie jest znane praktycznie wykonalne rozwiązanie. W przyszłości dopiszemy tu dodatkowe podrozdziały, aby wprowadzić niektóre z nich, ale w międzyczasie, jeśli jesteś zainteresowany, możesz zbadać niektóre z tych problemów (większość materiałów jest w języku angielskim):
- kolorowanie mapy i grafu w rozdziale 13 zbioru scenariuszy lekcji bez komputera (problem kolorowania grafu można zredukować do problemu planowania zajęć i na odwrót, pokazując, w jaki sposób problemy NP-zupełne mogą się ze sobą wiązać);
- problem plecakowy;
- problem pakowania pojemników;
- ścieżki Hamiltona (warto ten trudny problem skonfrontować z na pozór podobnym, lecz mającym praktycznie wykonalne rozwiązanie problemem istnienia szlaku Eulera, często przedstawianym jako problem siedmiu mostów);
- drzewa Steinera w rozdziale 15 zbioru scenariuszy;
- zbiory dominujące w rozdziale 14 zbioru scenariuszy;
- najdłuższa ścieżka -- Ten temat jest interesujący, ponieważ znalezienie najdłuższej ścieżki jest trudne, ale znalezienie najkrótszej ścieżki jest praktycznie wykonalne -- najkrótsza ścieżka jest obliczana, gdy urządzenie GPS wyznacza najkrótszą drogę do celu. Problem ścieżki Hamiltonona można łatwo zredukować do problemu najdłuższej ścieżki. Przy okazji można zapoznać się z koncepcją redukcji, pozwalającej jeden problem NP-zupełny użyć do rozwiązania innego. A oto piosenka na ten temat!
- problem gry w okręty.
Problem obliczalności jest ważny w informatyce -- wiąże się z zagadką powszechnie uważaną za największy nierozwiązany problem w informatyce. Może pamiętasz, że wspomnieliśmy, że są tysiące problemów, których praktycznie wykonalnego rozwiązania nie znamy, choć praktycznie wykonalne rozwiązanie dowolnego z nich można by dostosować do wszystkich innych. Mówiąc bardzo nieformalnie, ta grupa problemów nosi nazwę NP-zupełnych (jeśli naprawdę cię to ciekawi, NP jest skrótem od ,,non-deterministic polynomial'', a zupełność dotyczy tego, że wszystkie można przekształcić w siebie nawzajem!). Najważniejszym pytaniem jest to, czy istnieje algorytm wielomianowy rozwiązujący dowolny z nich, bo w takim wypadku wszystkie problemy z klasy NP miałyby rozwiązanie o czasie wielomianowym (czyli w klasie P). Pytanie to jest często jest formułowane tak: Czy P równa się NP?
Rzeczywistość jest gorsza, niż przedstawialiśmy powyżej. Do tej pory rozmawialiśmy problemach trudnych -- takich, które da się rozwiązać, ale które mogą wymagać miliardów lat pracy komputera. Jeśli uważasz, że to niedobrze, że niektóre problemy tak długo się rozwiązuje, to jeszcze nic! Istnieje kilka dobrze znanych problemów, których nigdy nie da się rozwiązać na komputerze. Na przykład, napisanie programu, który zawsze powie, czy inny program zakończy się, czy nie, jest niemożliwe! Oto inne przykłady takich problemów:
- http://www.cs4fn.org/algorithms/tiles.php
- http://www.cs4fn.org/algorithms/uncomputable.php
- http://www.cs4fn.org/algorithms/haltingproblem.php
Dobrze jest wiedzieć o tych sprawach, aby uniknąć próby pisania niemożliwych programów. To także fascynująca dziedzina badań, gdzie można dokonać odkryć, które mogłyby zmienić świat informatyki, a także przyczynić się do zrozumienia, co można, a czego nie można obliczyć.
Temat złożoności obliczeniowej i wykonalności jest bardzo dokładnie omawiany w sposób przystępny dla osób nie będących specjalistami, w popularnej książce Davida Harela Komputery -- spółka z o.o. Czego komputery naprawdę nie umieją robić (WNT 2011).
- Wikipedia -- złożoność obliczeniowa;
- gry z TSP (po angielsku);
- CS Unplugged -- ćwiczenie Kolorowanie grafów (po angielsku, z polską instrukcją);
- Wikipedia -- problem_komiwojażera;
- Wikipedia -- problem_plecakowy;
- Wikipedia -- inny problem związany z pakowaniem (po angielsku);
- Wikipedia -- graf_hamiltonowski;
- Wikipedia -- przeszukiwanie metodą siłową (po angielsku);
- CS Unplugged -- drzewa Steinera (po angielsku, z polską instrukcją);
- CS Unplugged -- zbiory dominujące (po angielsku, z polską instrukcją).