Jeśli kiedykolwiek zdarzyło ci się korzystać z arkusza kalkulacyjnego i wpisywać w nim formułę lub pisać programy, to jest bardzo prawdopodobne, że na pewnym etapie pisania system wyświetlił komunikat o błędzie i nie mógł zastosować się do twojego polecenia.
Są to błędy składni (po angielsku syntax errors). Te uciążliwe komunikaty są znane każdemu programiście. Oznacza to, że w czasie pracy popełnił błąd w składni jakiegoś polecenia. Błąd mógł być bardzo mały. Dla przykładu przypuścmy, że miałeś wpisać poniższą instrukcję:
x = (a+b)*(c+d)
ale przypadkowo zapomniałeś o jednym nawiasie:
x = (a+b)*c+d)
Kiedy spróbujesz skompilować lub skompilować i uruchomić program, wtedy komputer wyświetli informację, że wystąpił błąd. Jest to bardzo pomocne, w szczególności, gdy dostaniesz wskazówkę, gdzie ten błąd się znajduje. Do momentu jego naprawienia nie będziesz w stanie uruchomić programu.
Może się to wydawać irytujące, ale w rzeczywistości poprzez wymuszenie precyzji i dbałości o szczegóły, kompilator pomaga ci znaleźć błędy, zanim staną się one błędami w gotowym programie. W przeciwnym wypadku byłyby usunięte dopiero, gdy ktoś przetestowałby program i zauważył, że nie działa poprawnie.
Zawsze przy wystąpieniu takiego błędu masz do czynienia z językiem formalnym. Określają go ścisłe zasady, takie jak: „liczba otwierających nawiasów musi być taka sama jak zamykających”, „wszystkie polecenia w programie muszą być słowami kluczowymi wybranymi ze ściśle okreśłonego, małego zestawu” lub „data musi zawierać trzy liczby odseparowane myślnikami”.
Języki formalne nie są tylko używane w językach programowania — są one używane wszędzie tam, gdzie format danych wejściowych jest ściśle określony, na przykład wpisywanie adresu emailowego w formularz internetowy.
We wszystkich przypadkach, polecenia, które wpisujesz (czy to w Python, Scratch, Snap!, C, Pascal, Basic, C#, HTML, lub XML), są interpetowane przez program komputerowy. (Zgadza się… Python jest programem, który interpetuje programy napisane w języku Phyton). W rzeczywistości kompilator języka programowania jest często napisany w swoim własnym języku. Większość kompilatorów języka C jest napisana w C — co stawarza pytanie, kto napisał pierwszy kompilator C (i co jeśli miał on błędy)?! Informatycy odkryli dobre sposoby na pisanie programów, które przetwarzają inne programy, a najważniejsze przy tym jest dokładne określenie, co jest dozwolone w programie. Nad tym własnie czuwają języki formalne.
Wiele z koncepcji, którym będziemy przyglądać się w tym rozdziale, jest używanych w wielu innych sytuacjach: przy sprawdzeniu poprawności wpisanych danych na stronie internetowej; analizowaniu interfejsów użytkowników; przeszukiwaniu tekstu, w szczególności z wieloznacznikami, które mogą pasować do dowolnego ciągu znaków; tworzenia układów logicznych; określeniu protokołów komunikacyjnych; projektowaniu systemów wbudowanych. Niektóre zaawansowane koncepcje w językach formalnych wykorzystano do zbadania granic tego, co może zostać obliczone.
Gdy zapoznasz się z ideą języków formalnych, zobaczysz jakie jest to potężne narzędzie, dzięki któremu skomplikowane systemy można rozłożyć na mniejsze za pomocą prostych reguł.
Aby dać ci przedsmak tego, do czego można wykorzystać języki formalne, zacznijmy od poszukiwania słów, które pasują do konkretnych wzorców. Przypuśćmy, że szukasz słów, które zawierają imię tim. Wpisz słowo tim (lub kilka liter ze swojego imienia), następnie naciśnij przycisk „Wyszukaj słowa”, aby znaleźć wszystkie słowa zawierające frazę tim.
Teraz wprowadzimy znak wieloznaczny, w tym przypadku jest to kropka, który zastąpi nam dowolny symbol — jest to powszechnie stosowana konwencja w językach formalnych. Ten znak oznacza, że przypasować możemy do niego dowolną literę. Teraz możesz zrobić wyszukiwanie takie jak:
tim.b
i otrzymasz dowolne słowa, które mają zarówno tim oraz b z dowolnym pojedynczym znakiem w środku. Czy są jakieś słowa pasujące do tim..b? tim ...b? Możesz określić dowolną liczbę wystąpień symbolu, wstawiając za nim znak * (ponownie powszechnie używana konwencja), a więc:
tim.*b
wyszuka dowolne słowa, w których po tim następuje litera b, oddzielona dowolną liczbą znaków — być może nieoddzielona żadnym.
Spróbuj wykonać następujące wyszukiwanie. Jakie ciągi znaków zostaną znalezione?
x.*y.*z
- Czy możesz znaleźć słowa, które zawierają twoje imię lub inicjały?
- Co z słowami zawierającymi litery twojego imienia w prawidłowej kolejności?
- Czy są jakieś słowa, które zawierają wszystkie angielskie samogłoski w kolejności alfabetycznej (a, e, i, o, u)?
Kod, którego użyłeś powyżej, jest częścią języka formalnego zwanego wyrażeniem regularnym. Programy komputerowe, które mają za zadanie interpretowanie wpisanych danych wejściowych i ich akceptację, używają wyrażeń regularnych do sprawdzania elementów takich jak daty, numery kart kredytowych i kody produktów. Są szeroko używane przez kompilatory i interpretery języków programowania, aby zrozumieć tekst, który programista wpisuje.
Przyjrzymy się im bardziej szczegółowo w podrozdziale na temat wyrażeń regularnych.
Następnie zbadamy prosty system do odczytu danych wejściowych, o nazwie automat skończony, który — jak przekonamy się później — jest blisko związany z wyrażeniami regularnymi. Później przyjrzymy się idei gramatyki, która jest innym rodzajem języka formalnego, a która radzi sobie z bardziej skomplikowanymi formami danych wejściowych.
Oto mapa systemu kolei podmiejskich dla miasta Trainsylwania. Kłopot w tym, że nie pokazuje ona, dokąd jeżdżą pociągi — wiesz jedynie, że z każdej stacji odjeżdżają dwa pociagu, pociąg A i pociąg B. Mieszkańcom Trainsylvanii wydaje się to nie przeszkadzać — fajnie jest wybierać pociąg na każdej stacji, a po pewnym czasie i tak zwykle przyjeżdżasz tam, gdzie chciałeś.
Możesz podróżować po Trainsylwanii samodzielnie, korzystając z poniższej aplikacji. Zaczynasz od stacji City Mall i musisz znaleźć drogę do Suburbopolis. Na każdej stacji możesz wybrać pociąg A lub pociąg B — naciśnij przycisk, aby dowiedzieć się, dokąd cię zabierze. Prawdopodobnie, tak jak mieszkańcy Trainsylvanii, zaczniesz rysować mapę linii kolejowych, ponieważ później możesz zostać poproszony o znalezienie drogi w inne miejsce. Jeśli chcesz narysować szablon, możesz wydrukować go stąd.
Czy znalazłeś taką sekwencję pociągów, aby dostać się z City Mall do Suburbopolis? Aby się upewnić, że masz dobrą sekwencję, możesz ją wpisać poniżej, w celu sprawdzenia. Na przykład, jeśli skorzystałeś z pociągu A, następnie pociągu B, a następnie pociągu A, wpisz ABA.
Podróż po Trainsylwanii
Jeśli wybierzesz pociągi:
Czy potrafisz teraz znaleźć sekwencję, która zabierze cię z City Mall do Suburbopolis? Czy możesz znaleźć kolejną sekwencję, być może dłuższą? Przypuśćmy, że chcesz jechać naprawdę długą trasą. Czy znajdziesz sekwencję 12 przesiadek, która doprowadzi cię do celu? A 20 przesiadek?
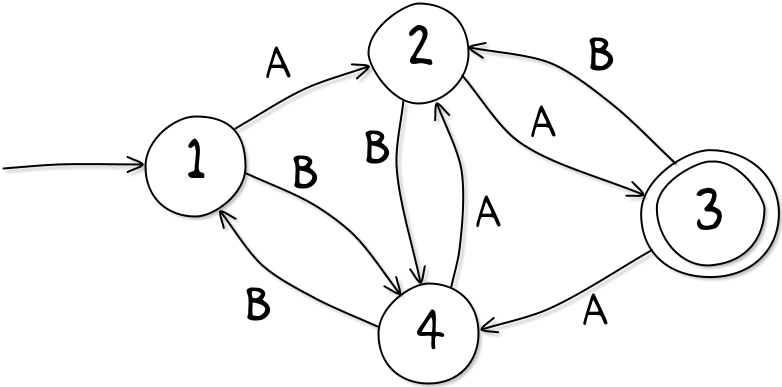
Oto kolejna mapa. Przedstawia inne miasto, a stacje mają tylko numery, a nie nazwy (oczywiście jeśli chcesz, możesz je nazwać).
Załóżmy, że zaczynasz od stacji 1 i musisz dostać się do stacji nr 3 (ma podwójne kółko, aby pokazać, dokąd zmierzasz).
- Jaka jest najkrótsza droga ze stacji 1 do stacji 3?
- Gdzie skończysz, jeśli zaczniesz od stacji 1 i jedziesz pociągami ABAA?
- Gdzie skończysz, jeśli zaczynasz na stacji 1 i wykonujesz 20 przesiadek, zawsze naprzemiennie A, B, A, B, A, B,...?
- Czy możesz podać łatwą do opisania sekwencję 100 lub więcej przesiadek, które doprowadzą cię do stacji nr 3?
Używana przez nas mapa z okręgami i strzałkami jest tak naprawdę czymś, co w informatyce nazywa się automatem skończonym, lub w skrócie AS (po angielsku FSA — Finite State Atomaton). Umiejętność korzystania z takich automatów jest bardzo przydatna dla informatyków.
-
Co to jest?. Automat skończony
Nazwa automat skończony (w skrócie AS) może wydawać się dziwna, ale znaczenie każdego słowa jest w zasadzie proste. „Automat” to stare słowo, oznaczające maszynę działającą samodzielnie, zgodnie z prostymi zasadami (takimi jak kukułka w zegarze z kukułką). „Skończony” oznacza po prostu, że jest ograniczona liczba stanów (takich jak stacje kolejowe na mapie).
Czasami AS jest nazywany maszyną skończoną (po angielsku FSM -- od Finite State Machine).
AS nie jest bardzo przydatny w przypadku map pociągów, ale notacja jest wykorzystywana do wielu innych celów, od sprawdzania danych wejściowych do programów komputerowych po kontrolowanie zachowania interfejsu. Być może natknąłeś się na to po wybraniu numeru telefonu, gdy otrzymałeś komunikat „Naciśnij 1, aby... Naciśnij 2, aby... Naciśnij 3, aby porozmawiać z operatorem”. Gdy naciskasz klawisze telefonu, wchodzisz do automatu skończonego na drugim końcu linii telefonicznej. Dialog może być dość prosty lub bardzo złożony. Czasami poruszasz się w kółko, ponieważ w automacie skończonym istnieje swoista pętla. Jeśli tak się dzieje, jest to błąd w konstrukcji systemu, co może być bardzo frustrujące dla dzwoniącego!
Innym przykładem jest pilot do klimatyzatora. Może mieć sześć głównych przycisków, a naciśnięcie przycisku zmienia tryb pracy (na przykład ogrzewanie, chłodzenie, automatyczny). Aby przejść do pożądanego trybu, musisz nacisnąć odpowiednią sekwencję. Jeśli naciśniesz o jeden przycisk za dużo, to tak, jakbyś już był na docelowej stacji kolejowej, ale przez przypadek wskoczył do jeszcze jednego pociągu. Za to twoja podróż powrotna na stację docelową może być bardzo długa i zakończona odkryciem wielu nowych sposobów, aby się tam dostać! Instrukcja obsługi pilota może zawierać diagram, który wygląda jak automat skończony. Jeśli nie ma instrukcji, możesz narysować mapę, tak jak w przypadku pociągów powyżej, abyś mógł lepiej zrozumieć, jak działa urządzenie.
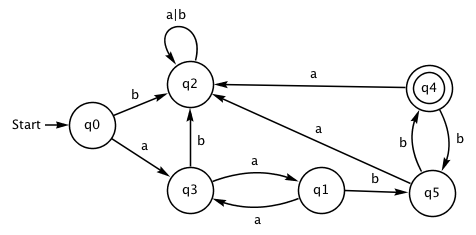
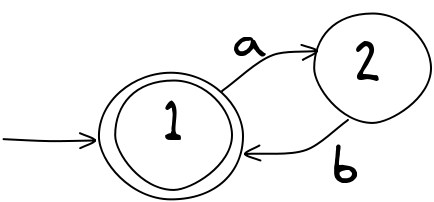
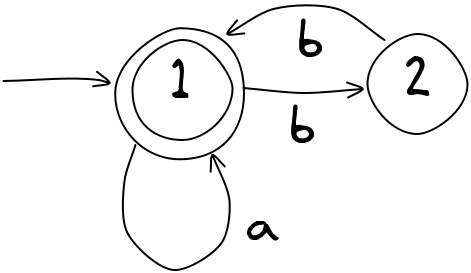
Mapa, której użyliśmy powyżej, korzysta ze standardowej notacji. Oto mniejsza:
Zwróć uwagę, że ta mapa ma trasy, które prowadzą bezpośrednio do miejsca, w którym się zaczęły! Na przykład, jeśli zaczynasz od 1 i wybierasz trasę b, natychmiast kończysz z powrotem w tym samym miejscu. To może wydawać się bez sensu, ale może być całkiem przydatne. Każda ze „stacji kolejowych” jest nazywana stanem, który jest ogólnym terminem oznaczającym miejsce, w którym znajdujesz się po sekwencji danych wejściowych lub decyzji. Jego rzeczywiste znaczenie zależy od tego, do czego służy dany AS. Stany mogą reprezentować tryb działania (taki jak szybki, średni lub wolny przy wyborze cyklu wirowania pralki) lub stan blokady lub alarmu (włączanie, wyłączanie, tryb wyjścia), lub wiele innych rzeczy. Wkrótce poznamy więcej przykładów.
Jeden ze stanów ma podwójne kółko. Zgodnie z konwencją oznacza to stan końcowy lub akceptujący. Jeśli tam dotrzemy, to osiągnęliśmy pewien cel. Jest też stan startowy — do którego dochodzi strzałka niewychodząca z żadnego stanu. W AS na ogół chodzi o to, aby znaleźć ciąg danych wejściowych, które doprowadzą cię od stanu początkowego do stanu końcowego. W powyższym przykładzie najkrótszym ciagiem wejściowym, pozwalającym przejść do stanu 2, jest a, ale możesz też tam dotrzeć poprzez aa, aba lub baaaaa. Mówimy wtedy, że te dane wejściowe są akceptowane, ponieważ potrafią nas przeprowadzić od stanu początkowego do stanu końcowego — nie musi to być najkrótsza droga.
W jakim stanie znalazłbyś się, gdyby dane wejściowe były literą a powtórzoną 100 razy?
Oczywiście, nie wszystkie dane wejściowe umożliwiają dojście do stanu 2. Na przykład aab lub nawet b nie są akceptowane przez ten prosty system. Czy potrafisz scharakteryzować, które dane wejściowe są akceptowane?
Oto aplikacja, która jest zgodna z zasadami powyższego AS. Możesz jej użyć do testowania różnych danych wejściowych.
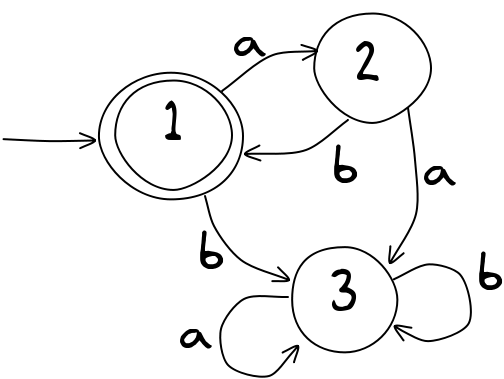
Oto kolejny AS, który wygląda podobnie do poprzedniego, ale zachowuje się zupełnie inaczej. Możesz przetestować go w aplikacji poniżej.
Sprawdź, które z poniższych wejść są akceptowane. Pamiętaj, aby za każdym razem zacząć od stanu 1!
- aaa
- abb
- aaaa
- bababab
- babababa
- litera a powtórzona 100 rzy
- litera a powtórzona 1001 razy
- litera b powtórzona milion razy, potem a, potem kolejny milion liter b
Czy możesz podać ogólną zasadę akceptacji danych wejściowych?
Aby zachować precyzję, zdefiniujemy dwa kolejne terminy. Jednym z nich jest alfabet, który jest po prostu listą wszystkich możliwych znaków wejściowych, które mogą wystąpić. W kilku ostatnich przykładach alfabet składa się z dwóch liter — a i b, ale w przypadku AS, który przetwarza tekst wpisany na komputerze, alfabet będzie musiał zawierać każdą literę występującą na klawiaturze.
Połaczenia pomiędzy stanami nazywane są przejściami, ponieważ następuje zmiana stanu. Ciąg znaków, które wprowadzamy do AS, jest często nazywany łańcuchem, zaś zbiór wszystkich łańcuchów, które mogą być zaakceptowane przez konkretny AS, nazywany jest jego językiem. W przypadku AS w ostatnim przykładzie jego język zawiera łańcuchy: a, aaa, bab, ababab i wiele więcej, ponieważ są one przez niego akceptowane. Jednak nie zawiera ciągów bb ani aa.
Język większości AS jest całkiem spory. AS, które właśnie oglądaliśmy, są nieskończone. Mógłbyś spędzić cały dzień, wypisując łańcuchy, które są akceptowane. Nie ma ograniczeń długości łańcuchów akceptowalnych.
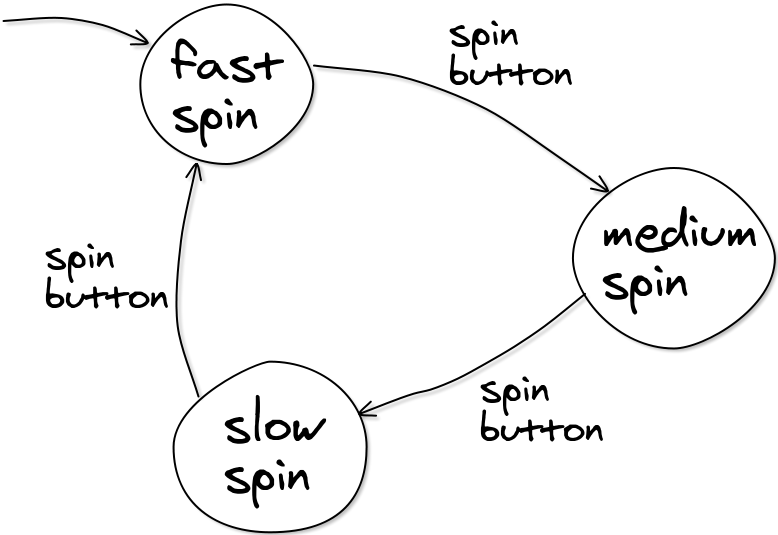
Jest to bardzo pożądane, ponieważ wiele prawdziwych AS ma do czynienia z dowolnie długimi danymi wejściowymi. Na przykład poniższy diagram pokazuje AS dla prędkości wirowania na pralce, gdzie każde naciśnięcie przycisku wirowania zmienia ustawienie.
Byłoby frustrujące, gdybyś mógł zmienić ustawienie wirowania tylko 50 razy, a potem dane wejściowe przestałyby być akceptowane. Jeśli chcesz, możesz przełączyć się z szybkiego na wolne wirowanie, naciskając przycisk wirowania 3002 razy. Zadziała również dwa razy. Lub 2 miliony razy (spróbuj, jeśli nie jesteś przekonany).
Poniższy diagram podsumowuje wprowadzoną przez nas terminologię. Zauważ, że ten AS ma dwa stany akceptujące. Może być ich tyle, ile potrzebujesz, ale zawsze tylko jeden stan początkowy.
W przypadku tego AS, łańcuchy aa i aabba byłyby akceptowane, w przeciwieństwie do aaa oraz ar. Zauważ, że r zawsze wraca do stanu 1 — jeśli kiedykolwiek wystąpi na wejściu, to zadziała jak reset.
Czasami zobaczysz AS nazywany maszyną skończoną lub FSM (z angielskiego Finite State Machine). Istnieją także inne ściśle powiązane systemy o podobnych nazwach. Wspomnimy o niektórych z nich później w tym rozdziale.
Teraz musimy coś wyjaśnić, zanim przejdziemy dalej. Jeśli rozważamy AS, w którym stan początkowy jest jednocześcnie stanem akceptującym, to pusty łańcuch — czyli ciąg bez żadnych liter — jest jednym z rozwiązań! Dla przykładu, oto prosty automat skończony z jednym tylko wejściem (przycisk a), który reprezentuje specyficzny rodzaj przełącznika światła. Przycisk resetowania nie jest częścią AS; to tylko sposób na powrót do stanu początkowego. Sprawdź, czy potrafisz określić, które rodzaje wejścia zapalą światło:
Czy odkryłeś, po których sekwencjach naciśnięć guzików światło jest zapalone? Teraz pomyśl o najkrótszej sekwencji od momentu zresetowania, po której światło jest zapalone.
Ponieważ światło jest już włączone po zresetowaniu, najkrótsza sekwencja jest pusta. Ponieważ trudno zapisać łańcuch o długości zero (chociaż można użyć „”), będziemy używać specjalnego symbolu, który jest grecką literą epsilon: \(\epsilon\). Często spotkasz się z \(\epsilon\) podczas nauki o językach formalnych.
Oto AS dla dziwnego przełącznika światła. Możesz powiedzieć, że \(\epsilon\) jest częścią języka, ponieważ stan początkowy jest również stanem końcowym (w rzeczywistości jest to jedyny stan końcowy). W rzeczywistości przełącznik nie jest wcale taki dziwny — rzutniki często wymagają dwóch naciśnięć przycisku zasilania, aby uniknąć ich przypadkowego wyłączenia.
W informatyce bardzo ważne jest rozważanie skrajnych przypadków. Jednym z ekstremalnych przypadków jest brak danych wejściowych: co zrobić, jeśli program otrzymuje pusty plik lub baza danych zawiera zero wpisów? Zawsze ważne jest, aby upewnić się, że te sytuacje zostały przemyślane przez twórców systemu. Nic więc dziwnego, że mamy symbol pustego łańcucha. Dodajmy, że niektórzy informatycy używają greckiej litery lambda (\(\lambda\)) zamiast \(\epsilon\), aby przedstawić pusty łańcuch znaków.
Nawiasem mówiąc, język powyższego trzystanowego AS jest nieskończenie duży, ponieważ jest zbiorem wszystkich łańcuchów, które zawierają potrójne wielokrotnosci litery a tzn. {\(\epsilon\), aaa, aaaaaa, aaaaaaaaa, ...}. To całkiem imponujące jak na taką małą maszynę.
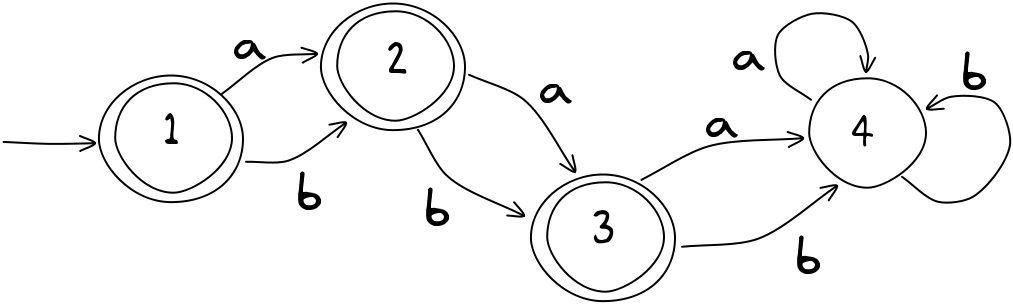
Skoro mówimy o skrajnościach, spójrzmy na kolejny AS. Używa on liter a i b jako swojego alfabetu.
Czy zaakceptuje on ciąg aaa? lub aba? Czy może cokolwiek z 3 lub więcej znakami?
Gdy przejdzie on do trzeciego znaku ciągu, znajdziesz się w stanie nr 4 który nazywa się stanem pułapki (po angielsku trap state), ponieważ nie możesz się z niego wydostać. Gdyby to była mapa dla systemu kolei podmiejskiej, który mieliśmy na początku tego rozdziału, spowodowałoby to problemy, ponieważ w końcu wszyscy znaleźliby się w stanie pułapki i mielibyśmy potężne przeludnienie na dworcu. Stan pułapki może być jednak bardzo przydatny w innych sytuacjach — szczególnie, gdy wystąpi błąd w danych wejściowych. Nieważne co wystąpi po błędzie, nie chcesz iść dalej.
W powyższym przykładzie językiem AS jest zbiór dowolnej kombinacji co najwyżej dwóch liter a i b. Nie zapominaj, że pusty ciąg jest również akceptowany. To bardzo mały język; jedynymi ciągami w nim są: \(\epsilon\), a, b, aa, ab, ba, bb.
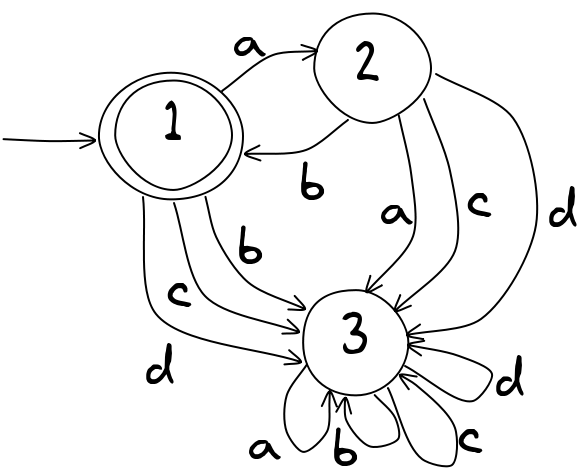
Oto kolejny AS do rozważenia:
Dość oczywiste jest to, co będzie akceptowane: łańcuchy takie jak ab, abab, abababababab i oczywiście \(\epsilon\). Ale są pewne brakujące przejścia: jeśli jesteś w stanie 1 i kolejnym znakiem jest b, nie masz dokąd iść. Jeśli dane wejściowe nie mogą zostać zaakceptowane, to zostaną odrzucone, tak jak w tym przypadku. Moglibyśmy wprowadzić stan pułapki, aby to wyjaśnić:
Rzeczy mogą się łatwo wymknąć spod kontroli. Co stałoby się, jeśli w alfabecie byłoby więcej liter? Potrzebowalibyśmy czegoś takiego:
Zamiast tego po prostu mówimy, że każde nieokreślone przejście powoduje odrzucenie danych wejściowych (tzn. zachowuje się tak, jakby przechodziło w stan pułapki). Innymi słowy, wystarczy użyć prostej wersji powyżej, z zaledwie dwoma przejściami.
Teraz, gdy mamy już uporządkowaną terminologię, przyjrzyjmy się kilku zastosowaniom tej prostej, ale potężnej „maszyny” zwanej automatem skończonym.
Automaty skończone są używane w projektowaniu obwodów cyfrowych (takich jak elektronika w dysku twardym) i systemach wbudowanych (takich jak alarmy antywłamaniowe lub kuchenki mikrofalowe). Wszystko, co ma kilka przycisków i przechodzi w różne stany po naciśnięciu tych przycisków (takich jak włączenie / wyłączenie alarmu, wysoka / średnia / niska moc) jest tak naprawdę pewnym rodzajem AS.
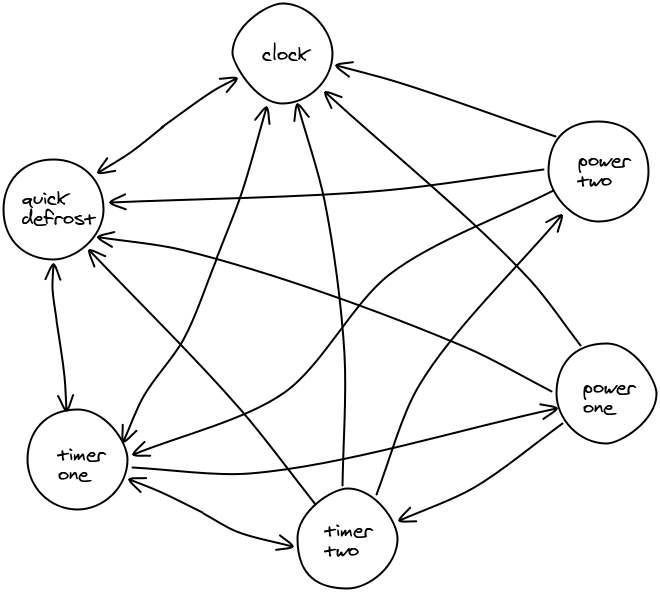
Przez to AS mogą być używane przez projektantów, aby zaplanować, co stanie się dla każdego wejścia w każdej sytuacji. Mogą być również wykorzystane do analizy interfejsu urządzenia. Jeśli AS opisujący urządzenie jest naprawdę skomplikowany, jest to ostrzeżenie, że interfejs prawdopodobnie nie będzie zrozumiały dla człowieka. Dla przykładu spórz na poniższy AS dla kuchenki mikrofalowej. Zwróć uwagę, że na przykład nie można przejść z power2 do power1 bez przechodzenia przez timer1. Tego typu ograniczenia mogą niektórych użytkowników frustrować. Na przykład, jeśli ktoś chciałby ustawić power1, to nie zadziała to, dopóki nie ustawi przedtem timer1. Po zapoznaniu się z tą sekwencją wszystko staje się łatwe, ale projektant powinien zastanowić się, czy konieczne jest zmuszenie użytkownika do tego rodzaju czynności. Tego rodzaju problemy stają się proste, gdy spojrzysz na AS. Właśnie wkroczyliśmy w obszar interakcji człowiek — komputer! Nie jest to zaskakujące, ponieważ większość dziedzin informatyki przenika się nawzajem — ale nie jest to aż tak ważne zastosowanie AS, więc wróćmy do bardziej powszechnych zastosowań.
Jak zobaczymy w następnym podrozdziale, jednym z najcenniejszych zastosowań AS w informatyce jest sprawdzenie danych wejściowych na komputerach, niezależnie czy jest to wartość wpisana w okienko dialogowe, program analizowany przez kompilator, czy też coś do wyszukania w dużym dokumencie. Istnieją również metody kompresji danych, które wykorzystują AS do przechwytywania wzorców w danych, które są kompresowane. Inne warianty AS symulują duże systemy komputerowe, aby sprawdzić, jak najlepiej je skonfigurować, zanim zostaną wydane pieniądze na ich budowę.
-
Ciekawostka. Największy AS na świecie
Jaki jest największy AS na świecie, który jest używany przez wiele osób każdego dnia? To jest Internet. Każda strona internetowa przypomina stan, a odnośniki na jej stronie są przejściami między nimi. W 2000 roku sieć miała miliard stron. W 2008 r. Google oświadczyło, że znalazło bilion różnych adresów stron internetowych. To dużo. Książka o miliardach stron miałaby grubość 50 km. Z bilionem stron jej grubość przekroczyłaby obwód Ziemi.
Ale Internet to tylko automat skończony. Abyś mógł korzystać z wyników wyszukiwarki internetowej, firmy takie jak Google muszą sprawdzić wszystkie strony, aby zobaczyć, jakie zawierają słowa. Badając sieć, podążają za wszystkimi odnośnikami, tak jak w przypadku podróży pociągiem. Ponieważ Internet nazywa się siecią, badanie nazywa się po angielsku crawling — to właśnie robią pająki.
To ćwiczenie polega na skonstruowaniu i testowaniu własnego AS, za pomocą bezpłatnego oprogramowania, które można pobrać samemu. Zanim to zrobimy, przyjrzymy się ogólnym sposobom tworzenia AS z danego opisu. Jeśli chcesz wypróbować użyte przykłady na „żywym” AS, przeczytaj kolejne dwa podrozdziały dotyczące używania Exorciser i JFLAP, które pozwolą ci na napisanie poniższych AS w jednym z programów i przetestowanie ich.
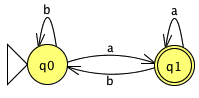
Dobrym punktem wyjścia jest pomyślenie o najkrótszym łańcuchu, który jest akceptowalny. Załóżmy na przykład, że potrzebujesz AS, który akceptuje wszystkie łańcuchy zawierające parzystą liczbę liter b. Najkrótszym takim ciągem jest \(\epsilon\), co oznacza, że stan początkowy musi również być stanem końcowym, więc możesz rozpocząć od narysowania tego:
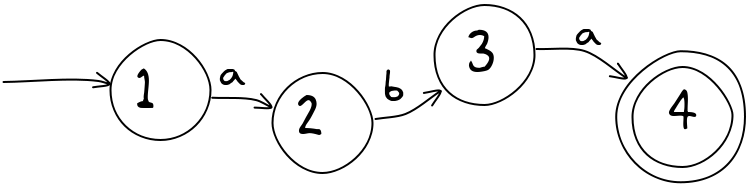
Jeśli zamiast tego musiałbyś zaprojektować AS, gdzie najkrótszym zaakceptowanym łańcuchem jest aba, potrzebowałbyś sekwencji 4 stanów, takich jak poniższe:
Następnie musisz pomyśleć, co dalej. Na przykład, jeśli akceptujemy tylko łańcuchy o parzystej liczbie b, to wtedy pojedyncze b musiałby przenieść cię od stanu początkowego do nieakceptującego:
Ale kolejne b spowoduje parzystość ciągu liter b, więc nasz AS musi taki łańcuch zaakcpetować. Każde kolejne b spowoduje przeniesienie się pomiędzy tymi dwoma stanami:
Zwykle każdemu stanowi można nadać „znaczenie”. W tym przykładzie bycie w stanie 1 oznacza, że do tej pory wprowadziłeś parzystą liczbę liter b, zaś stan 2 oznacza, że dotychczasowa ich liczba była nieparzysta.
Teraz musimy pomyśleć, czy nie brakuje nam jakichś przejść. Jak dotąd nie powiedzieliśmy maszynie, co ma robić w przypadku, gdy kolejnym znakiem łańcucha będzie litera a. Nasz AS ma akceptować parzystą liczbę liter b w łańcuchu, dlatego liczba liter a nie może wpływać na zmianę stanu:
To samo gdy automat znajduje się w stanie 2 i kolejnym znakiem jest litera a. Automat pozostaje w niezmienionym stanie:
Teraz każdy stan ma przejście dla każdego znaku wejściowego, więc AS jest gotowy. Przetestuj teraz AS na różnych przykładach, aby upewnić się, że zawsze parzysta liczba liter b w łańcuchu spowoduje przejście do stanu 1.
Wykonaj to ćwiczenie samemu, korzystając z poniższych instrukcji dla dwóch różnych programów, w celu zbudowania i przetestowania własnego AS.
W tym podrozdziale pokażemy, jak korzystać z oprogramowania edukacyjnego o nazwie „Exorciser”. (W następnym podrozdziale przedstawiamy alternatywę o nazwie JFLAP, która jest nieco trudniejsza w użyciu.) Exorciser ma udogodnienia do wykonywania zaawansowanych ćwiczeń związanych z językami formalnymi. Tutaj skupimy się tylko na tych najprostszych.
Exorciser może zostać ściągnięty stąd.
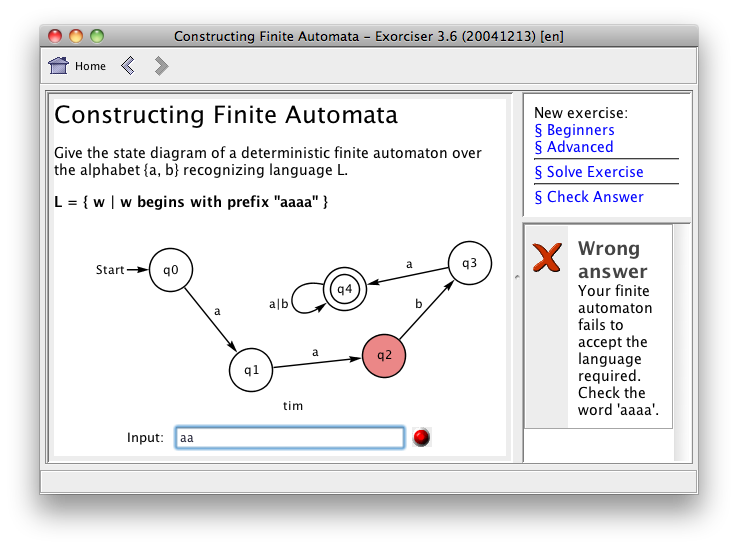
Po uruchomieniu wybierz „Konstruowanie automatów skończonych” (pierwszy element menu — Constructing Finite Automata); kliknij odnośnik „Początkujący” (Beginners), aby wykonać nowe ćwiczenie. Najtrudniejszą częścią każdego ćwiczenia związanego z budową AS jest oczywiście część po znaku „|” znajdującego się w nawiasach klamrowych. Na przykład na poniższym diagramie jesteś poproszony o narysowanie AS, który akceptuje łańcuch wejściowy w, jeśli w ma długość co najmniej 3. Powinieneś narysować i przetestować swoją odpowiedź. Na początku pomocne może okazać się kliknięcie „Rozwiąż ćwiczenie” (Solve exercise), aby uzyskać rozwiązanie. Następnie obserwowanie łańcuchów, które są akceptowane dla tego zadania. Tak właśnie zrobiliśmy, wykonując poniższy schemat.
Aby narysować AS w systemie Exorciser, kliknij prawym przyciskiem myszy w dowolne puste miejsce, a pojawi się menu dotyczące dodawania i usuwania stanów, wybierania alfabetu i tak dalej. Aby dokonać przejścia pomiędzy stanami, przeciągnij myszką od zewnętrznego kręgu jednego stanu do drugiego (lub wyjdź i wróć, aby stworzyć pętlę). Możesz kliknąć prawym przyciskiem myszy na stany i przejścia, aby je zmieniać. Zapis „a|b” oznacza, że przejście zostanie wykonane dla znaku a lub b (odpowiada to dwóm równoległym przejściom).
Jeśli twój AS nie rozwiąże zadanego problemu, otrzymasz podpowiedź w postaci łańcucha, którego AS nie akceptuje. Dzięki temu możesz go testować i poprawiać. Jeśli utkniesz, kliknij „Rozwiąż ćwiczenie” (Solve exercise). Możesz również śledzić dane wejściowe podczas pisania — kliknij prawym przyciskiem myszy, aby wybrać tę opcję. Na stronie SwissEduc możesz znaleźć więcej instrukcji.
Nieco dalej podajemy kilka przykładów do wypróbowania. Jeśli robisz to jako część projektu, zachowaj kopie automatów i testy, które wykonujesz. Kliknij wtedy prawym przyciskiem myszy, aby wybrać opcję „Zapisz jako” lub zrób zrzut ekranu z obrazkami.
Innym szeroko stosowanym programem do eksperymentowania z AS jest JFLAP (który można pobrać z http://jflap.org). Możesz użyć go jako alternatywy dla Exorcisera, jeśli to konieczne. Będziesz musiał postępować ostrożnie z instrukcjami, ponieważ ma o wiele więcej funkcji, niż potrzebujesz. Przez to może być trudno wrócić do miejsca, w którym zacząłeś.
Poniżej przedstawiamy instrukcję do stworzenia AS w JFLAP. Użyjemy następującego przykładu:
Aby stworzyć ten AS, uruchom JFLAP oraz:
- Kliknij przycisk „Finite Automaton” na panelu sterowania.
- W oknie edytora kliknij obrazek stanu (z niewielkim q na nim), a następnie kliknij w oknie, aby utworzyć stany.
- Aby przenieść stany, kliknij narzędzie ze strzałką na pasku narzędzi (ikonka najbardziej po lewej). Nie ma znaczenia, gdzie są stany, byle byłyby dobrze widoczne.
- Aby stworzyć przejście między dwoma stanami, kliknij narzędzie przejścia (trzecia ikonka), przeciągnij linię między dwoma stanami, wpisz etykietę przejścia (a lub b dla tego ćwiczenia) i naciśnij klawisz RETURN. (System zaoferuje pusty ciąg (\(\lambda\)) jako etykietę, ale prosimy nie wybieraj tego!)
- Aby zrobić pętlę powracającą do stanu, wystarczy kliknąć na stan za pomocą narzędzia przejścia.
- Możesz wybrać stan początkowy, wybierając narzędzie strzałki (ikonka najbardziej na lewo), klikając prawym przyciskiem myszy na stan i wybierając „Initial”. Tylko jeden stan może być stanem początkowym, ale możesz ustawić więcej niż jeden stan „Final” (akceptujący), klikając je prawym przyciskiem myszy.
Jeśli chcesz coś zmienić, możesz usunąć rzeczy za pomocą narzędzia do usuwania (ikonka czaszki). Ewentualnie wybierz narzędzie strzałki i kliknij dwukrotnie etykietę przejścia, aby ją edytować lub kliknij prawym przyciskiem myszki stan. Możesz przesuwać stany za pomocą narzędzia strzałki.
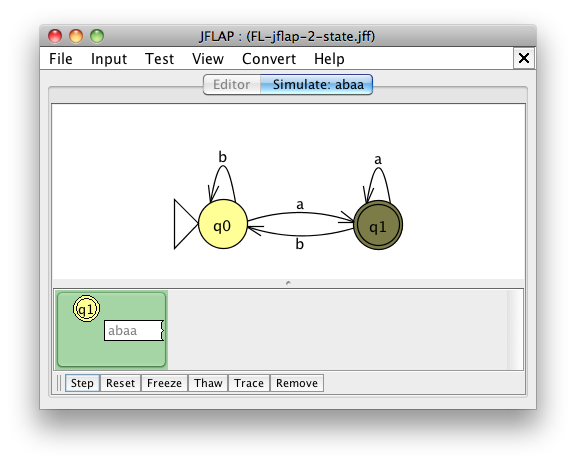
Aby zobaczyć, jak AS przetwarza dane wejściowe, użyj menu Input (u góry), wybierz „Step with closure”, wpisz krótki ciąg znaków, np. abaa i kliknij OK. Następnie w dolnej części okna możesz śledzić łańcuch znak po znaku, naciskając „Step”, który podświetla bieżący stan podczas przechodzenia przez łańcuch. Jeśli przejdziesz przez łańcuch i skończysz w stanie ostatecznym (akceptującym), panel zmieni się na zielony. Aby powrócić do okna edytora, przejdź do menu „File” i wybierz „Dismiss Tab”.
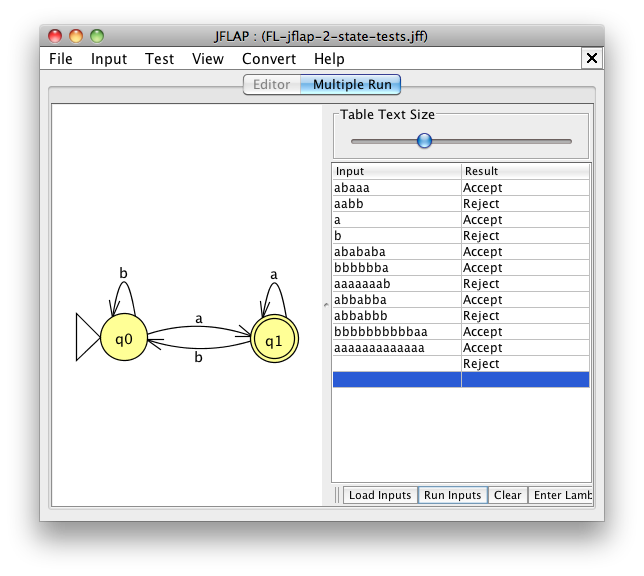
Możesz uruchomić wiele testów za jednym razem. Z menu „Input” wybierz „Multiple Run” i wpisz swoje łańcuchy testowe do tabeli lub załaduj je z pliku tekstowego.
Możesz nawet wykonać testy z pustym łańcuchem, pozostawiając pusty wiersz w tabeli, którą możesz zrobić, naciskając przycisk „Enter Lambda”.
W kolejnym podrozdziale podajemy kilka pomysłów na skonsturowanie AS. Jeśli robisz to jako część projektu, zachowaj kopie automatów i testów, które robisz (menu „File” i „Save Image As...”, aby zrobić zrzut ekranu, możesz też zapisać AS w postaci pliku, który można otworzyć i edytować później").
Korzystając z Exorciser lub JFLAP, skonstruuj AS, który pobiera dane wejściowe stworzone z liter a oraz b, i akceptuje dane wejściowe, jeśli spełniają poniższe wymaganie. Dla każdego z tych problemów powinieneś zbudować osobny AS.
- Łańcuchy rozpoczynające się od litery a (np. aa, abaaa i abbbb).
- Łańcuchy kończące się literą a (np. aa, abaaa i bbbba).
- Łańcuchy, które mają parzystą liczbę liter a (np. aa, abaaa, bbbb i nie zapominaj o pustym ciągu \(\epsilon\)).
- Łańcuchy, które mają nieparzystą liczbę liter a (np. a, baaa, bbbab, ale nie \(\epsilon\)).
- Łańcuchy, w których liczba a w danych wejściowych jest wielokrotnością trzech (np. aabaaaa, bababab).
- Łańcuchy, w których za każdym razem, gdy a pojawia się na wejściu, następuje b (np. abb, bbababbbabab, bbb).
- Łańcuchy, które kończą się na ab.
- Łańcuchy rozpoczynające się od ab i kończące na ba i tylko posiadające litery b w środku (np. abba, abbbbba).
W przypadku AS, które konstruujesz, sprawdź, czy akceptują prawidłowe dane wejściowe, ale również upewnij się, że odrzucają nieprawidłowe dane wejściowe.
Oto kilka sekwencji znaków, dla których możesz zbudować AS. Alfabet wejściowy to więcej niż a i b, ale nie musisz wprowadzać przejścia dla każdego możliwego znaku w każdym stanie, ponieważ AS może automatycznie odrzucić dane wejściowe, jeśli używa znaku, dla którego nie ustanowiłeś przejścia. Spróbuj wykonać dwa lub trzy z poniższych przykładów:
- Nazwy międzynarodowych standardowych rozmiarów papieru (od A1 do A10, od B1 do B10 itd.).
- Poprawna trzyliterowa nazwa miesiąca w języku angielskim (Jan, Feb, Mar itd.).
- Poprawny numer miesiąca (1, 2, ... 12).
- Prawidłowa angielska nazwa dnia tygodnia (Monday, Tuesday, ...).
Klasycznym przykładem AS jest automat sprzedający batoniki, który przyjmuje tylko kilka rodzajów monet. Załóżmy, że masz maszynę, która przyjmuje tylko monety 50 gr i 1 zł. Ty musisz włożyć 3 zł, aby kupić napój. Alfabet maszyny to moneta o nominale 50 gr i 1 zł, którą w skrócie nazwiemy odpowiednio G i Z. Na przykład, ZZZ wprowadzałby monety o sumie 3 zł, które byłyby akceptowane. ZGGZ również zostałoby zaakceptowane, ale ZGGG nie. Czy możesz zaprojektować AS, który akceptuje dane wejściowe, gdy 3 zł lub więcej zostanie wprowadzone do urządzenia? Możesz stworzyć własną wersję dla różnych nominałów monet i wymaganej sumy.
Jeśli miałeś do czynienia z liczbami binarnymi, zastanów się, jak działa poniższy AS. Wypróbuj każdą z podanych liczb binarnych jako dane wejściowe: 0, 1, 10, 11, 100, 101, 110, etc.
Czy możesz ustalić, co to znaczy, gdy dla danej liczby AS kończy się w stanie q1? Stanie q2?
-
Dodatkowe ćwiczenia. Automaty skończone w życiu codziennym
Istnieje wiele systemów wykorzystujących AS. Mógłbyś wybrać jakiś system i wyjaśnić, jak można go reprezentować za pomocą AS oraz pokazać przykłady sekwencji danych wejściowych, które są akceptowalne. Przykłady takich systemów to:
- Gry planszowe. Proste gry planszowe są często po prostu AS, gdzie następny ruch jest określony przez pewne dane wejściowe (np. liczbę z rzutu kostką), a stan końcowy oznacza, że ukończyłeś grę — czyli pierwsza osoba, która dotrze do stanu końcowego wygrywa. Większość gier jest zbyt skomplikowana, aby narysować pełną wersję AS, ale jako przykład można posłużyć się prostą grą, taką jak węże i drabiny. Jakie przykładowe sekwencje rzutów kostką doprowadzą cię do końca gry? A które nie?
- Proste urządzenia z kilkoma przyciskami często mają stany, które można łatwo zidentyfikować. Na przykład zdalne sterowanie alarmem samochodowym może mieć dwa przyciski. To, co dzieje się z samochodem, zależy od kolejności, w jakiej je naciskasz i aktualnego stanu samochodu (czy alarm w nim jest włączony, czy nie). W przypadku urządzeń, które automatycznie włączają się lub wyłączają po pewnym czasie, konieczne może być wprowadzenie danych wejściowych, takich jak „oczekiwanie przez 30 sekund”. Inne urządzenia do rozważenia to zegarki cyfrowe (z takimi stanami jak: „pokazywanie czasu”, „pokazywanie daty”, „pokazywanie stopera”, „stoper działa”), przyciski zasilania i wysuwania na odtwarzaczu CD, wybór kanału na pilocie telewizora (tylko liczby), ustawienie zegara, przechowywanie ustawień fabryczych w radiu samochodowym i panele kontrolne alarmów przeciwwłamaniowych.
-
Dodatkowe ćwiczenia. Biedronka Kara
SwissEduc ma środowisko programistyczne zwane Kara (do instalacji wymaga Javy), która jest programowalną biedronką. Krąży ona (w swojej najprostszej wersji) w wyimaginowanym świecie kontrolowanym przez automat skończony. Biedronka ma (symulowane) detektory, które wyczuwają jej bezpośrednie otoczenie; służą one jako dane wejściowe do AS.
Już posmakowaliśmy wyrażeń regularnych w podrozdziale wprowadzającym. Są one po prostu prostym sposobem wyszukiwania rzeczy w danych wejściowych lub określenia, jaki rodzaj danych wejściowych zostanie zaakceptowany jako poprawny. Na przykład wiele programów do obsługi skryptów internetowych używa ich do sprawdzania danych wejściowych dla wzorców, takich jak daty, adresy email i adresy URL. Stały się tak popularne, że są teraz wbudowane w większość języków programowania.
Być może podejrzewasz, że wyrażeniania regularne związane są z automatami skończonymi. I masz rację, ponieważ okazuje się, że każde wyrażenie regularne ma automat skończony, który może sprawdzić dopasowania, a każdy automat skończony może zostać przekonwertowany na wyrażenie regularne, które pokazuje dokładnie to, co akceptuje automat. Wyrażenia regularne są zwykle łatwiejsze do odczytania przez ludzi. W przypadku komputerów jest przeciwnie, dlatego program komputerowy konwertuje dowolne wyrażenie regularne na AS, a następnie komputer może bez problemu sprawdzić dane wejściowe.
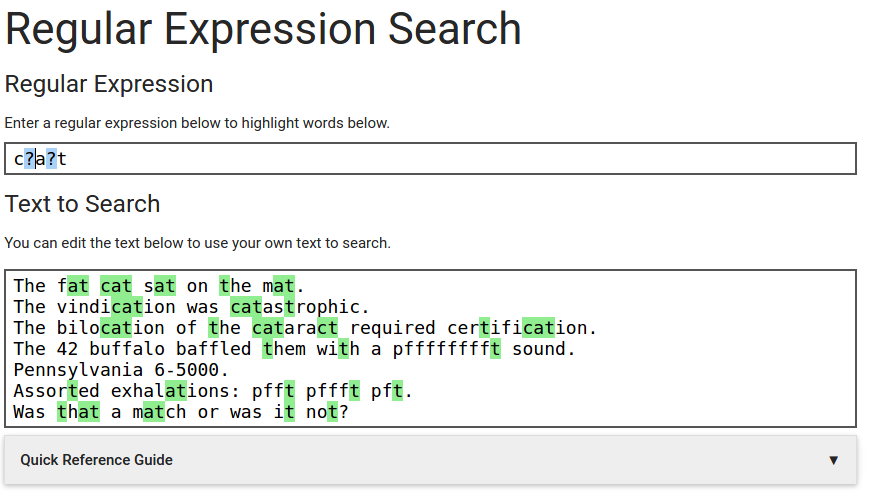
Najprostszym ćwiczeniem jest dopasowanie tekstu do wpisanego ciągu liter. Uruchom poniższą aplikację i wpisz tekst cat w polu oznaczonym „Wyrażenie regularne”:
Jeśli wpisałeś tylko trzy znaki cat, to powinno pojawić się 6 dopasowań.
Teraz spróbuj wpisać kropkę jako czwarty znak: „cat.”. W wyrażeniu regularnym „.” może zastępować dowolny pojedynczy znak. Spróbuj dodać więcej kropek przed i po cat. Co dzieje się dla cat.s lub cat..n? Przy okazji zauważmy, że czasem umieszczamy łańcuchy w cudzysłowach, aby było jasne, gdzie zaczynają się oraz kończą. Oczywiście cudzysłowy nie są częścią łańcuchów.
Co otrzymasz, jeśli wyszukujesz „ ... ” (trzy kropki ze spacją przed i po)?
Teraz spróbuj wyszukać „ic.”. Znak „.” pasuje do dowolnej litery, więc jeśli chcesz wyszukać kropkę, musisz napisać tak: „ic\.” — użyj tego wzoru wyszukiwania, aby znaleźć ic na końcu zdania.
Kolejny specjalny symbol to „\d”, który pasuje do dowolnej cyfry. Spróbuj wyszukać dwie, trzy lub cztery cyfry z rzędu (na przykład dwie cyfry z rzędu to „\d\d”).
Aby wybrać literę z małego zestawu znaków, używamy nawiasów kwadratowych. Spróbuj „[ua]ff”. Każdy ze znaków w nawiasach kwadratowych będzie pasował. Spróbuj napisać wyrażenie regularne, które będzie wyszukiwało wyrazy zawierające fat, sat i mat, ale nie cat.
Skrótem dla wyrażenia „[mnopqrs]” jest „[m-s]”. Wypróbuj również „[m-s]at” i „[4-6]”.
Kolejnym użytecznym skrótem jest możliwość wyszukiwania powtarzających się liter. Istnieją cztery powszechnie stosowane zasady:
- „a*” wyszukuje 0 lub więcej powtórzeń a.
- „a+” wyszukuje 1 lub więcej powtórzeń a.
- „a?” wyszukuje 0 lub 1 wystąpień a (to znaczy a jest opcjonalne).
- „a{5}” wyszukuje aaaaa (to znaczy, że a jest powtórzone 5 razy).
Spróbuj z nimi eksperymentować. Oto kilka przykładów, które warto wypróbować:
f+
pf*t
af*
f*t
f{5}
.{5}n
Jeśli chcesz wybrać między opcjami, przydatna jest pionowa kreska. Wypróbuj poniższe przykłady i sprawdź, do czego pasują. Możesz wpisać dodatkowy tekst w obszarze łańcucha testowego, jeśli chcesz eksperymentować:
was|that|hat
was|t?hat
th(at|e) cat
[Tt]h(at|e) [fc]at
(ff)+
f(ff)+
Zwróć uwagę na użycie nawiasów w celu grupowania części wyrażenia regularnego. Przydaje się to, jeśli chcesz zastosować „+” lub „*” do więcej niż jednego znaku.
-
Co to jest?. Wyrażenie regularne
Termin wyrażenie regularne jest czasami zapisywany skrótowo jako regex, regexp, lub RE. Jest ono regularne, ponieważ można je używać do definiowania łańcuchów znaków z bardzo prostej klasy języków, zwanych językami regularnymi. Jest wyrażeniem, ponieważ jest kombinacją symboli, zgodną z pewnymi zasadami.
Kliknij poniżej, aby wykonać kolejne ćwiczenie: Napisz krótkie wyrażenie regularne, pasujące do dwóch pierwszych słów, ale nie trzech ostatnich:
Zwykle wyrażenia regularne są używane do poważniejszych celów. Uruchom poniższą aplikację, aby uzyskać nowy tekst do wyszukania:
Poniższe wyrażenie regularne znajdzie typowe polskie tablice rejestracyjne (dla miast na prawach powiatu) w przykładowym tekście, ale czy możesz podać krótszą wersję, używając notacji „{n}"?
[A-Z][A-Z]\d\d\d\d\d
A jak znaleźć daty w tekście, przy zalożeniu, że miesiące są podane jako trzyliterowe skróty? Oto jedna z opcji, choć nie idealna:
\d [A-Z][a-z][a-z] \d\d\d\d
Czy możesz to poprawić?
A co z numerami telefonów? Musisz zastanowić się, jakie odmiany numerów telefonów są częste! Jak znaleźć adresy email?
Wyrażenia regularne są przydatne!
Szczególna forma wyrażen regularnych, których używaliśmy, została zaczerpnięta z języka programowania Ruby (popularnego języka do tworzenia stron internetowych), chociaż jest bardzo podobna do wyrażeń regularnych używanych w innych językach, w tym Java, JavaScript, PHP, Python i Microsoft .NET Framework. Nawet niektóre arkusze kalkulacyjne mają funkcje dopasowywania do wyrażenia regularnego.
Wyrażenia regularne mają swoje ograniczenia — na przykład, nie będziesz w stanie stworzyć takiego, który wyszukuje palindromom (słowa i frazy, które są takie same czytane zarówno od przodu jak i od tyłu, takie jak kajak, oko i atak kata). Nie można użyć jednego wyrażenia do wykrycia łańcuchów składających się z n powtórzeń litery a, po których następuje n powtórzeń litery b. Do tego typu wzorców potrzebny jest mocniejszy system, zwany gramatyką (zobacz rozdział o gramatyce). Niemniej jednak wyrażenia regularne są bardzo przydatne w typowym wyszukiwaniu wzorców.
Istnieje bezpośredni związek między wyrażeniami regularnymi i AS. Dla przykładu rozważ następujące wyrażenie regularne, które wyszukuje łańcuchy zaczynające się parzystą liczbą liter a i kończące się parzystą liczbą liter b:
(aa)+(bb)+
Teraz spójrz, jak następujący AS działa na tych łańcuchach — możesz spróbować aabb, aaaabb, aaaaabbbb, a także aaabb, aa, aabbb i tak dalej.
Być może zauważyłeś, że q2 jest stanem pułapki. Ten sam efekt możemy osiągnąć za pomocą następującego AS, w którym usunięto wszystkie przejścia do stanu pułapki — AS może odrzucić dane wejściowe, gdy nie ma pasującego do nich przejścia.
Tak jak AS, każde wyrażenie regularne reprezentuje język, które jest po prostu zbiorem wszystkich łańcuchów, które pasują do tego wyrażenia regularnego. W powyższym przykładzie najkrótszym łańcuchem w języku jest aabb, potem są aaaabb, aabbbb i tak dalej w nieskończoność. Istnieje również nieskończona liczba łańcuchów, które nie są w tym języku, jak a, aaa, aaaaaa i tak dalej.
W powyższym przykładzie AS jest naprawdę łatwym sposobem sprawdzenia wyrażenia regularnego — możesz napisać bardzo szybki i mały program, żeby to zaimplementować. To dobre ćwiczenie: tworzysz tablicę lub listę z wpisem dla każdego stanu, każdy wpis informuje cię, do którego stanu idziesz po każdym znaku, a także czy jest to stan ostateczny. Na każdym kroku program po prostu sprawdza, do którego stanu iść.
Na szczęście każde wyrażenie regularne można przekonwertować na AS. Nie przyjrzymy się, w jaki sposób jest to robione, ale zarówno Exorciser, jak i JFLAP mogą to zrobić za ciebie (zobacz ćwiczenia poniżej).
Większość języków programowania potrafi konwertować wyrażenia regularne na AS. Programiści zwykle używają wyrażeń regularnych, wywołując funkcje lub metody, którym przekazuje się wyrażenie regularne i szukany łańcuch. Kompilator konwertuje wyrażenie regularne na automat skończony. Po tym zadanie sprawdzenia twojego wyrażenia regularnego jest bardzo łatwe.
-
Projekt. Tworzenie wyrażeń regularnych
Oto kilka pomysłów na wyrażenia regularne, które możesz testować. Możesz je sprawdzić za pomocą wyszukuwania wyrażeń regularnych, tak jak to zrobiliśmy wcześniej, ale musisz stworzyć własny tekst,w którym wyrażenie będzie szukane. Testując wyrażenia, upewnij się, że nie tylko akceptują one poprawne łańcuchy, ale odrzucają te niepasujące, nawet jeśli brakuje tylko jednego znaku.
Możesz zmusić swoje wyrażenie regularne do wyszukiwania całego wiersza, wstawiając „^” (początek wiersza) przed wyrażeniem regularnym i „$” (koniec wiersza) za nim. Na przykład „^a+$” wyszukuje tylko wiersze, które składają się tylko i wyłącznie z liter a.
Możesz stworzyć wyrażenia regularne dla następujacych problemów:
- Lokalne tablice rejestracyjne (np. PO 12345 dla Poznania i np PGN 1234 dla powiatu gnieźnieńskiego).
- Dowolna rozszerzona forma słowa halo, np. haloooooooooooo.
- Warianty aaaarrrrrgggggghhhh.
- Zegar 24 godzinny (np. 23:00) lub 12 godzinny (np. 11:55 pm).
- Numer konta bankowego lub karty kredytowej.
- Data ważności karty kredytowej (musi mieć 4 cyfry, np. 01/15).
- Hasło, które musi zawierać co najmniej 2 cyfry.
- Data.
- Numer telefonu (wybierz swój format, np. tylko telefon komórkowy, numery krajowe lub międzynarodowe).
- Kwota w złotych wpisana na stronie banku, która powinna akceptować różne formaty, np. „21,43 zł”, „21”, „21,43PLN”, i „5.000PLN”, ale nie „zł21”, „21.5”, „5,0000.00” i „PLN300”.
- Akceptowalne nazwy zmiennych w twoim języku programowania (zwykle coś w rodzaju litery, po której następuje kombinacja liter, cyfr i niektórych znaków interpunkcyjnych).
- Liczba całkowita w twoim języku programowania (pozwól na „+” i „-” z przodu, a niektóre języki pozwalają na przyrostki takie jak L lub przedrostki takie jak 0x).
- Adres IP (np. 172.16.5.2 lub 172.168.10.10:8080).
- Ades MAC urządzenia (np. e1:ce:8f:2a:0a:ba).
- Kody pocztowe dla kilku krajów np. Nowej Zelandii: 8041, Kanady: T2N 1N4, USA: 90210, Polski 60614, 60-614.
- (niektóre) adresy URL http, takie jak „http://abc.xyz”, „http://abc.xyz#wnioski”, „http://abc.xyz?search=fgh„”.
-
Projekt. Konwertowanie wyrażeń regularnych na AS
W tym projekcie utworzysz wyrażenie regularne, skonwertujesz je na AS i pokażesz, jak przetwarzane są niektóre łańcuchy.
Jest jeden drobiazg, o którym musisz wiedzieć: oprogramowanie, z którego korzystamy poniżej, nie ma wszystkich notacji, których używaliśmy powyżej, które są powszechne w językach programowania, ale nie są używane w teorii języków formalnych. W rzeczywistości jedynymi dostępnymi są:
- „a*" wyszukuje zero lub więcej powtórzeń a.
- „a|b" wyszukuje a lub b.
- „(aa|bb)*" daje mieszaninę par liter a i par liter b. Nawiasy grupują polecenia.
Ograniczenie do tych trzech notacji nie jest problemem, gdyż wszystkie inne można uzyskać korzystając z nich. Na przykład „a+” jest tym samym co „aa*”, a „\d” to „0|1|2|3|4|5|67|8|9”. Będzie to trochę powolne, ale nie będzie to dużą uciążliwością, bo w ćwiczeniach są proste.
Kowersja z Exorciser
Skorzystaj z tej części, jeśli używasz Exorciser, który jest zalecany dla tego projektu, ale jeśli używasz JFLAP, przejdź do Konwersja z JFLAP poniżej.
Exorciser jest bardzo prosty. Jeśli nie zmienisz ustawień domyślnych, może on konwertować tylko wyrażenia regularne, używając dwóch znaków: a i b. Ale nawet to wystarczy (teoretycznie każde wejście może być reprezentowane dwoma znakami — to tak jak w liczbach binarnych!).
Na dodatek Exorciser ma dostępny symbol pustego łańcucha — jeśli wpiszesz e, zostanie przekonwertowany na \(\epsilon\). Na przykład „(a| \(\epsilon\))” oznacza opcjonalne a w danych wejściowych.
Aby wykonać ten projekt za pomocą Exorciser, przejdź do okna startowego („home”) i wybierz drugie łącze „Regular Expression to Finite Automata Conversion” (Konwersja wyrażenia regularnego na automaty skończone). Teraz wpisz swoje wyrażenie regularne w polu wprowadzania tekstu zaczynającym się od „R=”.
Na rozgrzewkę spróbuj:
aabbpotem kliknij „Solve exercise” (rozwiąż ćwiczenie), to jest pójście na skróty — oprogramowanie jest przeznaczone dla uczniów do tworzenia własnych AS, ale to wykracza poza ramy tego projektu. Powinieneś otrzymać bardzo prosty AS!
Aby przetestować AS, kliknij prawym przyciskiem myszy tło i wybierz „Track input” (Śledź wejście).
Teraz spróbuj niektórych bardziej złożonych wyrażeń regularnych, takich jak poniższe. Dla każdego z nich wpisz je, kliknij „Solve exercise” (rozwiąż ćwiczenie), a następnie prześledź kilka przykładowych danych wejściowych, aby zobaczyć, jak AS akceptuje i odrzuca różne łańcuchy.
aa*b a(bb)* (bba*)* (b*a)*aTwój raport z projektu powinien: pokazywać wyrażenia regularne, wyjaśniać, jakie rodzaje łańcuchów pasują do nich, pokazywać odpowiednie AS, pokazywać sekwencję stanów, przez które przechodzą niektóre łańcuchy próbne, a następnie powinieneś wyjaśnić, w jaki sposób komponenty AS odpowiadają częściom wyrażenia regularnego (za pomocą przykładów).
Konwertowanie z JFLAP
W JFLAP możesz używać prawie dowolnego znaku jako danych wejściowych. Głównymi wyjątkami są „*”, „+” (mylące: „+” jest używany zamiast „|” dla alternatywy) i „!” (który jest pustym łańcuchem — w preferencjach, które możesz wybrać, ustaw, czy ma być pokazywany jako \(\lambda\) lub \(\epsilon\)).
Głównymi operatorami dostępnymi w JFLAP są:
- „a*” wyszukuje zero lub więcej powtórzeń a.
- „a+b” wyszukuje a lub b.
- „(aa+bb)*” Nawiasy grupują polecenia; w tym przypadku daje mieszaninę par liter a i par liter b.
Oprogramowanie JFLAP może współpracować z różnymi językami formalnymi, więc musisz zignorować wiele opcji, które oferuje!
W tym samouczku (po angielsku) są pewne szczegóły dotyczące formatu, który JFLAP wykorzystuje do wyrażeń regularnych — wystarczy przeczytać rozdział rozdziały „Definition” i „Creating a regular expression”.
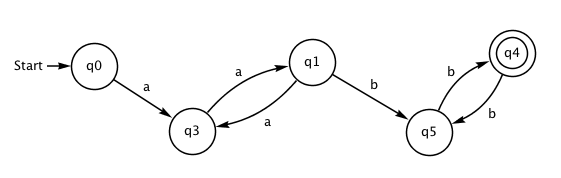
W ramach rozgrzewki przekształcimy poniższe wyrażenie regularne w AS:
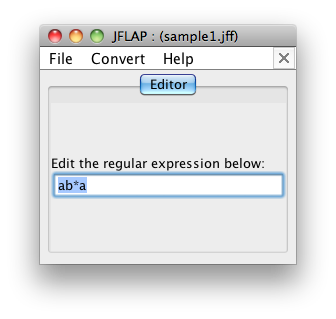
ab*bW głównym oknie kontrolnym JFLAP kliknij „Wyrażenie regularne” i wpisz swoje wyrażenie regularne do JFLAP:
Teraz wypróbuj kilka przykładowych danych wejściowych. Stan początkowy jest oznaczony jako q0 i ma dużą strzałkę wskazującą na niego. Możesz zmusić JFLAP, aby przeszedł przez niektóre dane wejściowe za pomocą menu „Input” (Wejście). „Step by state” (Następny stan) będzie podążał za twoim wejściem stan po stanie, „Fast run” (Szybkie uruchamianie) pokaże sekwencję odwiedzonych stanów dla twojego wejścia, a „Multiple run” (Wielokrotne uruchamianie) umożliwia załadować listę łańcuchów do przetestowania.
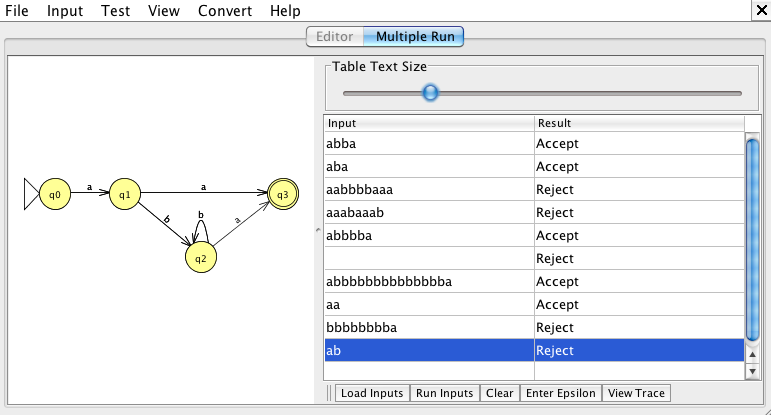
Wielokrotne uruchomienie dobrze nadaje się do wykonania wielu testów dla twojego wyrażenia regularnego:
Na przykład ab zostaje odrzucone, ponieważ dojdzie tylko do stanu 2.
Teraz powinieneś wymyślić własne wyrażenia regularne, które przetestują interesujące wzorce i wygenerują dla nich AS. W JFLAP możesz utworzyć AS dla niektórych wyrażeń regularnych, których użyliśmy wcześniej, takich jak (proste) daty, adresy email lub adresy URL.
Jeśli konwersja wyrażeń regularnych na AS jest częścią projektu, to powinieneś pokazać wyrażenia regularne, wyjaśniać, jaki rodzaj łancuchów pasuje do nich, pokazać odpowiadający AS, pokazać sekwencję stanów, przez które przechodzą niektóre łańcuchy próbne, a następnie powinieneś wyjaśnić, w jaki sposób komponenty AS odpowiadają częściom wyrażenia regularnego (za pomocą przykładów).
-
Projekt. Inne pomysły na projekty i ćwiczenia
Oto kilka pomysłów, które można wykorzystać do zbadania wyrażeń regularnych:
Na stronie regexdict przeczytaj instrukcję (po angielsku) na temat dopasowywania do wzorców i napisz wyrażenia regularne do wyszukiwania słów takich jak:
- Słowa zawierające aa.
- Wszystkie słowa z 3 literami.
- Wszystkie słowa z 8 literami.
- Wszystkie wyrazy zawierające więcej niż 8 liter.
- Słowa zawierające litery twojego imienia.
- Słowa, które składają się z liter które występują w twoim imieniu.
- Słowa zawierające wszystkie samogłoski w odwrotnej kolejności.
- Słowa, które można stworzyć za pomocą tylko nut na pianinie (tj. liter od A do G i od a do g).
Polecenie Znajdź w Microsoft Word używa wyrażeń regularnych po wybraniu opcji „Użyj symboli wieloznacznych”. Aby uzyskać więcej informacji, przeczytaj artykuł „Znajdowanie i zastępowanie znaków za pomocą symboli wieloznacznych” (po angielsku) Grahama Mayora.
Odkryj wyrażenia regularne w arkuszach kalkulacyjnych. Arkusz kalkulacyjny Google docs ma funkcję RegExMatch, RegExExtract i RegExReplace. W Excelu są one dostępne przez Visual Basic.
Dziewiarskie wzory są formą wyrażeń regularnych. Jeśli interesuje cię dziewiarstwo, możesz sprawdzić, jak są one ze soba powiązane, w artykule o dzianinie i wyrażeniach regularnych na stronie CS4FN.
Polecenie grep jest dostępne w wierszach poleceń wielu systemów operacyjnych i wyszukuje tekst zgodny z wyrażeniem regularnym w pliku wejściowym. (Nazwa pochodzi od „Global Regular Expression Parser” — globalny parser wyrażenia regularnego)). Zademonstruj działanie polecenia grep dla różnych wyrażeń regularnych.
Funkcje dopasowania względem wyrażeń regularnych pojawiają się w większości języków programowania. Jeśli twój ulubiony język ma tę funkcję, możesz pokazać, jak to działa, używając przykładowych wyrażeń regularnych i łańcuchów.
Zaawansowane: Darmowe narzędzia lex i flex mogą przyjmować specyfikacje dla wyrażeń regularnych i tworzyć programy analizujące dane wejściowe zgodnie z regułami. Są one powszechnie używane jako część interfejsowa kompilatora, a dane wejściowe to program, który jest kompilowany. Możesz zbadać te narzędzia i zademonstrować prostą implementację.
Pamietasz Yodę z „Gwiezdnych wojen”? Ma on bardzo osobliwy sposób mówienia. Jednak wciąż potrafisz go zrozumieć. Elastyczność reguł gramatyki angielskiej (jak i polskiej) oznacza, że zazwyczaj możesz zostać zrozumiany, nawet jeśli nie mówisz całkiem poprawnie, ale oznacza to również, że reguły są bardzo skomplikowane i trudne do zastosowania.
Gramatyki w językach formalnych są znacznie bardziej przewidywalne niż gramatyki w językach naturalnych. Dlatego nazywa się je językami formalnymi! Kiedy mówisz po angielsku, gramatyka może sprawiać ci wiele trudności. Istnieje wiele reguł i wiele wyjatków od tych reguł — na przykład potrzebujesz apostrofu, jeśli piszesz „the computer's USB port”, ale musisz go pominąć, jeśli powiesz „its USB port”.
Gramatyki w informatyce są używane głównie do określania języków programowania i formatów plików. Przez nie kompilatory robią problemy, nawet jeśli pominiesz tylko jeden nawias lub przecinek! Równocześnie są one bardzo przewidywalne.
Ten podrozdział zamierzamy rozbudować w przyszłości i wtedy przyjrzymy się gramatykom powszechnie stosowanym w informatyce. Są one bardzo wydajne, ponieważ sprawiają, że bardzo skomplikowany system (jak kompilator języka lub format HTML) jest określony w bardzo zwięzły sposób. Ponadto są programy, które automatycznie, korzystając z gramatyki, zbudują system dla ciebie. Gramatyki dla konwencjonalnych języków programowania nie są dobrym pomysłem, aby użyć ich jako początkowych przykładów, więc będziemy pracować z kilkoma małymi przykładami, w tym z częściami gramatyk dla języków programowania.
Uwaga: pozostała część tego podrozdziału nie została jeszcze opracowana.
Ten rozdział jest tylko zarysem tego, co można robić, wykorzystując języki formalne. Jeśli uznałeś materiał w tym rozdziale za interesujący, oto kilka tematów, które możesz chcieć zgłębić.
Języki formalne pojawiają się w różnych dziedzinach informatyki i są bardzo przydatnymi narzędziami dla naukowców zajmujących się komputerami. Redukują one niewiarygodnie złożone systemy do niewielkiego opisu i odwrotnie, umożliwiają stworzyć bardzo złożone systemy z kilku prostych zasad. Są one niezbędne do pisania kompilatorów, a więc są aktywowane za każdym razem, gdy ktoś pisze program! Są one również związane z teorią automatów i teorią obliczalności, są też w pewnym stopniu wykorzystywane w komputerowym przetwarzaniu języka naturalnego.
W podrozdziale Automaty a wyrażenia regularne korzystaliśmy z AS, które tak naprawdę są deterministycznymi automatami skończonymi (DFA), ponieważ decyzja o tym, którego przejścia należy dokonać, jest jednoznaczna na każdym etapie.
Zdarza się także, że okresla się takie AS jako akceptor skończony, ponieważ akceptuje i odrzuca dane wejściowe w zależności od tego, czy osiąga stan końcowy. Istnieją różne warianty automatów, o których nie wspominaliśmy, w tym maszyny Mealy'ego i Moore'a (które generują dane wyjściowe dla każdego dokonanego przejścia lub osiągniętego stanu), zagnieżdżona maszyna stanów (gdzie każdy stan może być AS samym w sobie), niedeterministyczne automaty skończone (które mogą mieć tę samą etykietę na więcej niż jednym przejściu poza stan) i lambda-NFA (które mogą zawierać przejścia na pustym ciągu, \(\lambda\)). Wierzcie lub nie, wszystkie te odmiany są w zasadzie równoważne i można je przekształcać jedne na drugie. Są one wykorzystywane w wielu praktycznych sytuacjach do projektowania systemów dla przetwarzania danych wejściowych.
Jednak istnieją również bardziej złożone modele obliczeń, takie jak automat PDA (Push-Down Automaton), który jest w stanie przestrzegać reguł gramatyk bezkontekstowych i najbardziej ogólny model obliczeń zwany maszyną Turinga. Modele te są coraz bardziej złożone i abstrakcyjne, a struktury takie jak maszyna Turinga nie są wykorzystywane jako urządzenia fizyczne (z wyjątkiem zabawy). Zamiast tego są wykorzystywane jako narzędzie do wnioskowania o tym, co można obliczyć. W zasadzie każdy komputer jest rodzajem ograniczonej maszyny Turinga, więc ograniczenia, które odnoszą się do maszyny Turinga, stanowią ograniczenia w codziennych obliczeniach.
Maszyna Turinga została tak nazwana na cześć Alana Turinga, który pracował nad teoretycznymi podstawami informatyki w połowie lat trzydziestych XX wieku (to ten sam Turing, którego nazwiskiem nazwano test badający sztuczną inteligencję -- prace Turinga pojawiają się w wielu obszarach informatyki!). Jeśli chcesz poznać ideę maszyny Turinga i lubisz czekoladę, zrób ćwiczenie na stronie CS4FN, które ilustruje, jak ona działa.
Środowisko programowania Kara również oferuje przykłady działania maszyny Turinga
W tym rozdziale omówiliśmy jeden z dwóch głównych rodzajów języka formalnego: wyrażenie regularne. Drugim (który w omówimy w przyszłości) jest gramatyka bezkontekstowa. Oba są typami typami języków, które są szeroko stosowane w kompilatorach i systemach przetwarzania plików. Wyrażenia regularne wykorzystuje się do znajdowania prostych wzorców w pliku, takich jak słowa kluczowe i liczby w programie lub znaczniki w pliku HTML, lub daty i adresy URL w formularzu internetowym. Gramatyki bezkontekstowe są dobre, gdy musisz się zmierzyć z zagnieżdżonymi strukturami, na przykład, gdy wyrażenie składa się z innych wyrażeń lub gdy instrukcja jeżeli zawiera blok zdań, które z kolei mogą być wyrażeniami jeżeli, ad infinitum.
Istnieją bardziej zaawansowane formy gramatyki, na przykład gramatyki kontekstowe i nieograniczone gramatyki, w których przejścia od stanu do stanu zależą nie od jednego, a od kilku znaków. Przykładowo mógłbyś mieć
xAy \(\to\) aBb,
co jest bardziej elastyczne, ale o wiele trudniejsze w obsłudze. Relacje między głównymi rodzajami gramatyk opisał językoznawca Noam Chomsky. Na jego cześć klasyfikację języków formalnych nazwano hierarchią Chomsky’ego.
Istnieje bezpośrednia zależność między „maszynami” (takimi jak AS) i językami (takimi jak wyrażenie regularne), ponieważ każdy coraz bardziej złożony język potrzebuje odpowiednio złożonej maszyny do jego przetworzenia. Na przykład, AS może być użyty do określenia, czy dane wejściowe pasują do danego wyrażenia regularnego, ale PDA jest potrzebne, aby do CFG dopasowany został ciąg. Teoria języków formalnych analizuje te relacje i wymyśla sposoby tworzenia odpowiednich maszyn dla danego języka i odwrotnie.
Dostępnych jest wiele narzędzi, które będą czytać specyfikację dla danego języka i tworzyć inny program do analizowania języka; są to na przykład Lex i Flex (oba wykonują leksykalną analizę wyrażeń regularnych), Yacc („yet another compiler compiler”) i Bison (ulepszona wersja Yacc). Te programy sprawiają, że stosunkowo łatwo jest stworzyć własny język programowania i skonstruować dla niego kompilator, chociaż wymagają one sporej gamy umiejętności, aby wszystko działało!
Dopiero zaczęliśmy mówić o tym, co można zrobić w językach formalnych, ale intencją tego rozdziału jest zasygnalizowanie zagadnień, którymi zajmują informatycy, oraz uświadomienie czytelnikowi, że istnieją potężne narzędzia, które zostały stworzone, aby mieć możliwość pracy z nieskończenie złożonymi systemami przy użyciu niewielkich opisów.
Inspiracją dla niektórych materiałów z tego rodziału była ta strona. Na stronie i-Programmer (po angielsku) jest bardzo dobry artykuł o AS.
Podręczniki o językach formalnych zawierają znacznie bardziej zaawansowany materiał i mają większy matematyczny rygor, niż wymagany w szkole średniej, ale dla uczniów, którzy naprawdę chcą czytać więcej, dobra jest książka Wprowadzenie do teorii obliczeń Michaela Sipsera (WNT 2016).
Wyrażenia regularne i ich relacje z AS są dobrze wyjaśnione w książce Algorytmy Roberta Sedgewicka (Helion 2017).
Poniższe materiały sa po angielsku.
- Wikipedia -- język formalny;
- Wikipedia -- gramatyki bezkontekstowe;
- Wikipedia -- drzewo składniowe;
- Wikipedia -- wyrażenie regularne;
- CS Unplugged -- automaty skończone;
- i-Programmer -- maszyny skończone;
- JFLAP;
- Wikipedia -- automat deterministyczny;
- Wikipedia -- maszyna skończona.
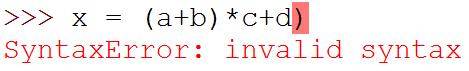












![Wait, forgot to escape a space. Wheeeeee[taptaptap]eeeeee. Komentarz xkcd do kreskówek o wyrażeniach regularnych](../images/xkcd-regular-expressions.png)